微元法在修正几何光学命题中的应用
2011-01-24余红岩
余红岩
(衢州市龙游第二高级中学 浙江 衢州 324400)
解决物理问题,关键是物理方法和数学方法的有机结合,物理方法突出发散思维,数学方法突出抽象思维.微元法是物理学中常用的一种方法,既体现了物理思维,又体现了数学思维,可以解决物理学中常见的错误命题.
学习了折射定律后,有这样一道题,用微元法解之,会发现命题的缺陷.
原题:如图1所示,光从空气射向上下表面平行的玻璃砖时,入射角为i,经折射从下表面射出.设玻璃砖的折射率为n,厚度为h,发生的侧移为D.试证明入射角i越大,侧移D越大.
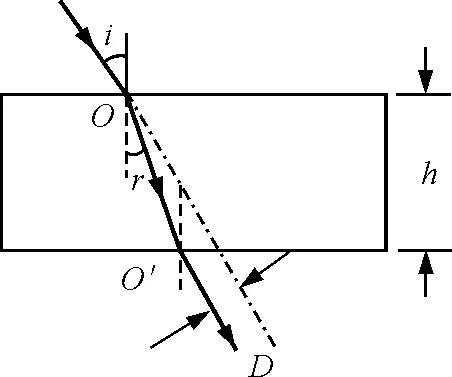
图1
参考解答:设在第一界面,光在玻璃砖中的折射角为r,由折射定律有
(1)
由数学知识可知
(2)
(3)
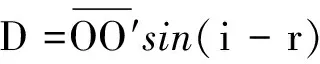
(4)
sin(i-r)=(sinicosr-sinrcosi)
(5)
综合(1)、(2)、(3)、(4)、(5)式得
(6)
由(6)式可知,当入射角i增大,侧移D增大.
对(6)式,单从解答上来说,无可非议.但是我们仔细分析时,却发现了问题.
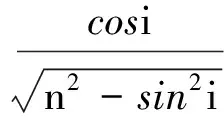
微元法解答:
由(1)式可知
sini=nsinr
等式两边微分有
d(sini)=nd(sinr)
即有
cosidi=ncosrdr
由n>1,i>r,cosr>cosi可得
di>dr
与(3)、(4)对比,列式可知
(7)
(8)
(9)

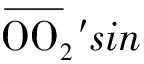
(10)
di>dr
(11)
由于
cos(r1+dr) 代入式(7)、(9)两式,故得 (12) 又因 di>dr 故有 sin[(i1-r1)+(di-dr)]>sin(i1-r1) (13) 综合(8)、(10)、(12)、(13)式得 D1 即当入射角i增大,侧移D增大. 笔者认为在中学物理阶段,不涉及高等数学知的前提下求解,原命题应作以下修改: 如图1所示,光从空气射向上、下表面平行的玻璃砖上,入射角为i,经折射最终从下表面射出,设玻璃砖的折射率为n,厚度为h,发生的侧移为D,己知n2≫sin2i,试证明入射角为i越大,侧移D越大. 参考文献 1 刘大华.小量分析在中学物理中的应用.物理教学,2008 (2) : 39
