从竞赛题到高考题

王鹤新

(江阴市第一中学 江苏 江阴 214400)

高考题与竞赛题之间的渊源，已有几年的历史.竞赛题在高考中的不断变相出现和高考物理改革的深化是相一致的，旨在加强对学生能力的考查，在近几年江苏自主命题的高考物理试卷中尤为突出.那么，这类高考题是怎样从竞赛题演变来的呢？下面列举几例说明.

1 创设相同情境通过问题铺垫降低难度

【竞赛题1】长为2l的轻绳，两端各系有一质量为m的小球，中点系有质量为M的小球，三球成一直线置于光滑水平桌面上，绳处于伸直状态.对小球M施以冲力，使其获得与绳垂直的初速度v0，如图1所示.试求：

(1)两小球m相碰时绳中张力T；

(2)若从小球M开始运动到两小球m相碰的时间为t，在此期间内小球M经过的距离sM[1].

图1

解析:(1)当两小球m相碰时，M运动方向上动量守恒.设m沿M运动方向上速度为v1，相碰时垂直v1方向速度为v2,则

Mv0=(2m+M)v1

又由机械能守恒有

得

对M应用牛顿第二定律

相碰时m以M为参考点做圆周运动(非惯性参考系，引入惯性力)，对m

(2)在M运动方向上平均动量守恒

即

【高考题1】(2005年高考江苏物理卷第18题)如图2所示，三个质量均为m的弹性小球用两根长均为L的轻绳连成一条直线而静止在光滑水平面上.现给中间的小球B一个水平初速度v0，方向与绳垂直.小球相互碰撞时无机械能损失，轻绳不可伸长.求：

(1)当小球A，C第一次相碰时，小球B的速度;

(2)当三个小球再次处在同一直线上时，小球B的速度;

(3)运动过程中小球A的最大动能EKA和此时两根绳的夹角θ;

(4)当三个小球处在同一直线上时，绳中的拉力F的大小.

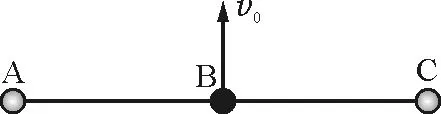
图2

解析:(1)设小球A,C第一次相碰时，小球B的速度为vB(方向为初速度v0方向)，考虑到对称性及绳子的不可伸长特性，小球A,C沿小球B初速度方向的速度也为vB.由动量守恒定律得

mv0=3mvB

(2)当三个小球再次处在同一直线上时，由动量守恒定律和能量守恒定律得

mv0=mvB+2mvA

解得

vA=0(初态)

vB=v0(初态)

图3

(3)当小球A的动能最大时(C的动能也最大)，小球B的速度为零，设此时小球A,C的速度大小为u(因为vB=0，A,C与B沿绳子方向的分速度相等，所以A,C速度与绳子垂直)，两根绳的夹角θ为(图3)，由动量守恒定律和能量守恒定律得

得小球A的最大动能

此时两根绳的夹角θ=90°.

(4)小球A,C均以半径L绕小球B做圆周运动，当三个小球在同一直线上时，以小球B为参考系(小球B的加速度为零，为惯性参考系)，小球A,C相对于小球B的速度均为

v=|vA-vB|=v0

所以，此时绳中的拉力为

【点评】通过对竞赛题的多个设问，实现了竞赛题向高考题的过渡.

共同点：创设了相同的物理情境，利用了相同的物理模型.运用了相同的物理规律,如系统动量守恒、能量守恒、圆周运动规律及牛顿第二定律等.

不同点：设问不同，回避了一种拿到高考题却无从下手的现象.所以对于学生来讲，思维的跳跃有所降低，但设问由浅入深、层层递进.

高考题中间球的质量M换成了m，化过程的计算“繁琐”为“简单”.

竞赛题中研究的是相碰时绳中张力T(此时中间M球是非惯性系)，而高考题中研究的是一直线时绳中张力T(此时aB=0，B是个惯性参考系)，化“纲外”为“纲内”.

2 创设相同情境通过增设条件降低难度

【竞赛题2】如图4所示，在空间有相互垂直的匀强电场E和匀强磁场B，一电子从原点静止释放，求电子在y轴方向前进的最大距离.(不计电子重力)[1]

图4

解析:电子从静止释放到最大距离的过程中，小球做的是一般的曲线运动.可以进行“零速度分解”：可以设想为具有x轴正方向的速度+v与x轴负方向的速度-v，其中+v满足

qvB=qE

小球在+x轴方向的洛伦兹力与电场力相平衡.小球在水平方向做速度为v的匀速直线运动.由于水平向左的速度-v产生竖直向上的洛伦兹力，小球在xOy平面内做速度为v的匀速圆周运动.所以小球在xOy平面内的运动可以看成是水平向右速度为v的匀速直线运动与xOy平面的匀速圆周运动的合运动.方向上具有独立性与等时性.

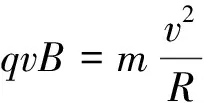
【高考题2】(2008年高考江苏物理卷第14题)在场强为B的水平匀强磁场中，一质量为m、带正电q的小球在O点静止释放，小球的运动曲线如图5所示.已知此曲线在最低点的曲率半径为该点到x轴距离的2倍,重力加速度为g.求:

(1)小球运动到任意位置P(x,y)的速率v;

(2)小球在运动过程中第一次下降的最大距离ym.

图5

解析:(1)根据动能定理

(2)由提问中看出：第一次下降最大距离时，小球速度大小为vm，方向为水平方向.

根据动能定理

对最低点

【点评】通过对竞赛题中电场力与重力的类比，增设了“曲率半径”这个条件，实现了过渡.

共同点：创设了相同的物理情境，利用了相同的物理模型,实现了相同的物理过程.

不同点：其实对于竞赛题而言，有三种处理方法：平均值法、微元法、零速度分解.但是这三种方法对于学生而言，难度都很大.为了降低难度，高考题增设了“曲率半径”这个条件.同样高考题还在第二问的基础之上，利用了类比的思想，加设了一问,突出了类比思想的重要地位.

3 创设相同情境通过条件简化降低难度

【竞赛题3】如图6所示,从高H处的同一点先后平抛两球1和2.球1直接经竖直挡板的顶端落到水平地面B点，球2与地面的A点碰撞后经竖直挡板的顶端，第二次落到水平地面B点.设球2与地面的碰撞是弹性碰撞,求竖直挡板的高度h[1].

解析:设1球从抛出点到B点的时间为t1，有

设2球从抛出点到A点的时间为t2，有

1,2两球从抛出点到B点的整个过程，水平方向

v1t1=3v2t2

v1=3v2

又因两球飞过竖直挡板的水平位移相同

图6

【高考题3】(2008年高考江苏物理卷第13题)抛体运动在各类体育运动项目中很常见，如乒乓球运动.现讨论乒乓球发球问题.

设球台长2L、网高h，乒乓球反弹前后水平分速度不变，竖直分速度大小不变、方向相反，且不考虑乒乓球的旋转和空气阻力(设重力加速度为g).

(1)若球在球台边缘O点正上方高度为h1处以速度v1水平发出，落在球台的P1点(如图7实线所示)，求P1点距O点的距离x.

(2)若球在O点正上方以速度v2水平发出后,恰好在最高点时越过球网落在球台的P2点(如图7虚线所示),求v2的大小.

图7

(3)若球在O点正上方水平发出后，球经反弹恰好越过球网且刚好落在对方球台边缘P3处，求发球点距O点的高度h3.

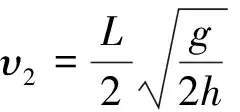
(3)如图8所示，发球高度为h3，飞行时间为t3.同理根据平抛运动

图8

设球从恰好越过球网到最高点的时间为t，水平距离为s，有

由几何关系知x3+s=L，解得

【点评】竞赛题与高考题创设了相同的物理情境，利用了相同的物理模型，实现了相同的物理过程，反映了相同的物理知识点.

共同点：都利用了平抛运动分解的思想，利用了两段平抛运动的水平位移之和等于某一常量.都利用了恰好越过网端与恰好越过挡板的顶端.

不同点：竞赛题利用了两个小球的平抛运动，但具有不同的速度.而高考题进行了简化，利用了一个小球的平抛运动，而且其中的一个水平位移直接告知.高考题对弹性碰撞做了解释，其物理情境更加生活化，更体现了新课程物理源于生活，服务于生活.

高考与竞赛的确存在一定的渊源.我们可以借助竞赛题的一些特殊的物理情境、物理模型和一些物理过程，而且要充分挖掘他们之间的区别，化“纲外为纲内”、化“烦”为“简”、化“普遍”为“特殊”等去充分培养学生的思维能力;又不能一味地依懒于竞赛，一味地追求难度，不能舍本求末.所以如何在高考复习中把握好“度”的问题是个关键.通过竞赛题的引入，进而为高考服务.

参考文献

1 范小辉.新编奥林匹克物理竞赛指导.南京：南京师范大学出版社，2003