巧用运动合成分解法解决复杂问题
2011-01-24张锦科
张锦科
(张家川县第二中学 甘肃 天水 741506)
在中学物理教学中,不仅要注重物理基础知识的教学,注重对学生进行基本的解题原理、解题方法和思路的训练,而且有必要使学生理解和掌握一些典型的科学思维方法和解题技巧.对于同一个物理问题,往往能从不同的角度去思考和分析,采用不同的方法来解决,但繁简程度却可能有很大的区别.如果遵循一定的科学思维方法,掌握一定的解题技巧,则往往会事半功倍,得心应手.
运动的合成与分解是研究运动的基本方法,是将复杂的、生疏的运动分解成简单的、熟悉的运动进行研究的方法,这是一种技能.这种处理问题的方法可以变曲线运动为直线运动,变复杂运动为简单运动,从而使问题的解决得到明显的简化.
【例1】 一质点从高处自由下落距离h后,落到倾角为45°很长的光滑斜面上,并与斜面发生多次弹性碰撞(图1).选取直角坐标,重力加速度为g.求:
(1)经过n次(n=1,2,3,…)碰撞后刚弹起时速度的x分量和y分量;
(2)任意两次碰撞之间的时间间隔.

图1
解析:小球的运动可分解为沿斜面向下加速度为a∥=gsin45°的匀加速运动和垂直斜面加速度为a⊥=gcos45°的来回反弹运动,如图1所示(类似相对于斜面的竖直上抛运动).
小球与斜面每连续碰撞两次之间的时间间隔就等于小球在垂直斜面方向上来回运动一次的时间.由于在垂直斜面的方向上,任一来回小球的位移为零,沿这个方向的分力不做功,因此每次与斜面碰前或碰后瞬间,在垂直斜面方向上的分速度的大小始终不变,即相邻碰撞两次之间的时间间隔是相等的.
设小球第一次与斜面碰前瞬间速度为v0,则
(1)
(2)
根据“反射定律”,第一次碰后的速度v0是水平的.把v0分别沿斜面和垂直斜面分解作为两个分运动的初始速度.即沿斜面为v1∥=v0cos45°,垂直于斜面为v1⊥=v0sin45° .
设每两次碰撞之间的时间间隔为Δt,根据前面分析有
(3)
第n次与斜面碰撞,小球所经历的时间为
tn=(n-1)Δt
(4)
设此时沿斜面的分速度为vn,则
vn=v0cos45°+a∥tn=
v0cos45°+gsin45°(n-1)Δt
(5)
建立直角坐标系,第n次碰后瞬间垂直斜面方向的分速度和沿斜面的分速度分别如图1所示.因此水平速度为
vx=vncos45°+v0sin45°sin45°
(6)
联立(2)、(3)、(5)、(6)式,得
竖直速度为
vy=vnsin45°-v0sin45°cos45°
(7)
联立(2)、(3)、(5)、(7)式,得
点评:在教学中要利用不同类型的典型题进行一题多解的训练活动,这样不仅可以破除学生的定势思维,也可以拓宽学生的视野和思路,达到举一反三、触类旁通的目的;还可以激发学生学习的浓厚兴趣,有利于培养学生思维的敏捷性和变通性.在解题训练过程中,要有意指明解题的思想方法和各方法的特点,以及在解决不同问题时的优势和不足.学习物理就要学习物理思想和研究问题的方法,这样才能在学习物理知识的过程中培养能力,才能适应时代,不断创新.
【例2】如图2所示,倾角为α的光滑斜面固定在地面上不动,一个小钢球以角β飞向斜面,试问β为何值时,球可以返回到它第一次与斜面相碰的点?(所有碰撞都可认为是弹性的)

图2
解析:小球的运动可分解为沿斜面向上的匀减速运动(往返)和垂直斜面的来回反弹运动,如图2所示.小球如能回到入射点,则由机械能守恒定律知,小球回到该点时的速度大小与入射时的速度大小相等.设小球第一次碰撞的速度为v,小球回到入射点时与斜面碰撞了n次,经历时间为t,由平行斜面方向的运动
由垂直斜面方向的运动
联立两式可得
解得
β=arccot(ntanα) (n=1,2,3,…)
点评:本题分别将速度和加速度沿斜面和垂直斜面分解,直接导致了解题的便捷.因此在实际中,要培养学生打破“平抛”分解模式,灵活地分解,从而达到巧妙、简洁地解题目的.对比例1和例2,说明题目虽千变万化,但万变不离其宗,这“宗”即解题的思想方法.
【例3】 制备纳米薄膜装置的工作电极可简化为真空中间距为d的两平行极板,如图3(a)所示.加在极板A,B间的电压UAB做周期性变化,其正向电压为U0,反向电压为-kU0(k>1),电压变化的周期为2τ,如图3(b)所示.在t=0时,极板B附近的一个电子,质量为m,电荷量为e,受电场作用由静止开始运动.若整个运动过程中,电子未碰到极板A,且不考虑重力作用.

(2)若电子在0~200τ时间未碰到极板B,求此运动过程中电子速度v随时间t变化的关系;
(3)若电子在第N个周期内的位移为零,求k的值.

图3
解析:(1)电子在0~τ时间内做匀加速运动,加速度的大小为
(8)
位移
(9)
在τ~2τ时间内先做匀减速运动,后反向做匀加速运动,加速度的大小
(10)
初速度的大小
v1=a1τ
(11)
匀减速运动阶段的位移
(12)
依据题意d>x1+x2,解得
(13)


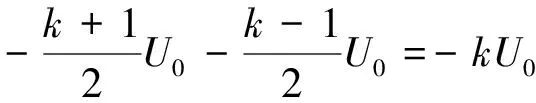
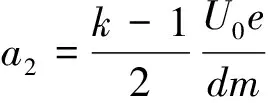

图4

t-2nτ(0≤t-2nτ<τ) (n=0,1,2, …,99)
因此
v2n+1=a1(t-2nτ)
(14)
v2n+1'=a2t
(15)
故合速度为
u2n+1=v2n+1-v2n+1'=a1(t-2nτ)-a2t=

t-(2n+1)τ
[0≤t-(2n+1)τ<τ] (n=0,1,2, …,99)
因此v2n+2=a1τ-a1[t-(2n+1)τ]
(16)
v2n+2'=a2t
(17)
故合速度为
u2n+2=v2n+2-v2n+2'=
a1τ-a1[t-(2n+1)τ]-a2t=
(3)矩形电压场中电子在第N个周期内的位移为v-t图像[图4(b)]中一个周期三角形的面积即
(18)
稳恒电压场中电子反向运动的位移为前N个周期的位移减去前(N-1)个周期的位移即

(19)
依题意xN-xN'=0
(20)
联立解得

点评:2010年江苏高考压卷题偏难,颇有竞赛题风格.参考答案数学味太浓,很多学生看完答案后不知所云.利用分解与合成的方法,使对试题的理解变得容易,有效减小了思维量.对称矩形场中电子的运动我们比较熟悉,即先向上匀加速再向上匀减速运动,而且两段对称,做题时要充分利用这一结论.
