一种改进的Gabor算法及其在人脸识别中的应用

薛晓利，胡 蓉，朱金陵

(1.西南交通大学 电气工程学院，成都 610031;2.成都电子机械高等专科学校 通信工程系，成都 610071)

人脸识别是生物特征鉴别技术的主要方向之一，它涉及图像处理、模式识别、计算机视觉等各个领域。相对其他诸如指纹识别、虹膜识别等人体生物识别技术而言，人脸识别具有直接、容易接受、侵犯性小，较少或不需要用户主动配合等特点，因此，人脸识别技术已经成为近年来最热门的研究领域。然而，由于受到光照、姿态、表情等因素的影响，人脸识别技术远没有达到实际应用的水平。其中，预处理、特征提取、分类器设计3个环节显得尤为重要。本文将从特征提取的角度出发，提出一种基于Sobel边缘增强的Gabor小波变换算法，并将其成功应用在人脸识别中。

1 Sobel算子

Sobel算子是一种一阶差分离散算子，主要用于边缘检测和边缘增强。在图像上的任意像素点运算该算子，就可以得到对应的梯度矢量或其法向量。Sobel算子主要包含2组的矩阵，分别为横向和纵向，将其与图像做卷积就得到横向和纵向的亮度差分近似值。如果以I(x)来代表原始图像，Gx(x)和Gy(x)分别代表横向和纵向边缘检测的梯度图像，则:

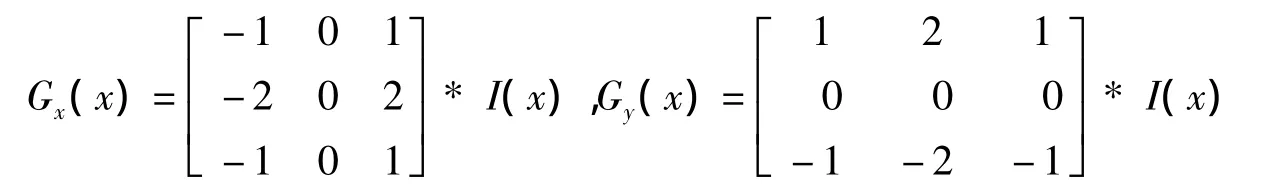
图1 原图及其梯形图

2 Gabor小波变换

Gabor特征通常采用一系列Gabor滤波器组来提取，一般选用5×8，4×8和3×8等［4，11］。研究人员比较了Gabor特征和几何特征的识别性能，发现Gabor特征具有更好的识别性能。正因为如此，近年来，Gabor变换作为一种有效的工具被广泛应用于图像处理、模式识别等相关领域。一般来说，用2D的Gabor核函数进行特征提取，其定义为:

本文中，vmax=5，μmax=8，σ =2π。这里，σ决定了高斯窗口的宽度与波长之间的比率。因此，给定一幅图像I(z)，其Gabor变换Gj(z)定义为该图像与上述Gabor核函数之间的卷积:Gj(z)=I(z)* Ψj(z)，这里 z=(x，y)表示图像的坐标位置。Gj(z)表示以v为频率、以μ为方向的卷积结果，该卷积结果是一个复数，可以表示为:Gj(z)=Aj(z)·exp(iθj(z))。其中，Aj(z)表示幅度，θj(z)表示相位。采用上面定义的40个Gabor核函数对该图像进行卷积来得到Gabor实部和虚部特征，如图2所示。

图2 40个Gabor特征

3 人脸识别预处理

在人脸识别中，预处理是个非常重要的过程。本文的预处理主要是根据双眼坐标位置进行人脸图片的旋转、裁剪、矫正，其过程包含以下4个步骤:

1)手工定位双眼瞳孔位置坐标。

2)根据左右眼的位置坐标，旋转图片，使得双眼处于水平位置，从而保证人脸方向的一致性。

3)根据双眼位置坐标，确定人脸面部区域。

4)将人脸图像缩放到同一个尺度大小。本文中将其缩放到70×70大小。

这里，采用Caltech、ORL、Yale、Bioid人脸库来进行测试。预处理结果如图3所示。

图3 原图与预处理结果的比较

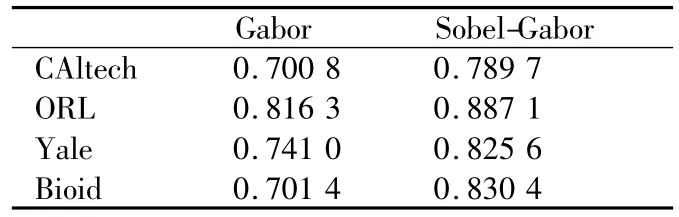
表1 2种算法的人脸识别结果比较

4 实验结果及结论

本文将Sobel-Gabor算法分别在Caltech人脸库、ORL人脸库、Yale人脸库、Bioid人脸库上进行测试。详细测试步骤如下:

1)根据手工标定的双眼瞳孔位置坐标，进行人脸裁剪、旋转、对齐、缩放操作。

2)将人脸图像同Sobel算子做卷积，得到对应的梯度图;

3)在人脸梯度图上，进行Gabor小波变换，从而得到表征人脸的特征矢量V(x);

4)对任意两个人脸图片I1(x)和I2(x)，分别计算其特征矢量V1(x)和V2(x);

5)用卡方距离χ2来计算两个矢量之间的不相似度，即:

将本文提出的Sobel-Gabor算法结果同基于Gabor算法的人脸识别结果进行对比，其测试结果如表1所示。结果表明:同基于Gabor小波变化的人脸识别算法相比，本文提出的Sobel-Gabor算法能显著提高识别率，说明了该算法的有效性。

［1］万峰，杜明辉.人脸识别中一种新的Gabor特征提取方法［J］.华南理工大学学报，2004，32(8):5-8，17.

［2］LEE T S.Image representation using 2D Gabor wavelets［J］.IEEE Transaction on Pattern Analysis and Machine Intelligence，1996，18(10):959.

［3］LIU C，WECHSLER H.Gabor feature based classification using the enhanced fisher linear discriminant model for face recognition［J］.IEEE Transaction on Image Processing，2002，11(4):467.

［4］DONATO G，BARTLETT M S，HAGER J C，et al.Classifying facial actions［J］.IEEE Transaction on Pattern Analysis and Machine Intelligence，1999，21(10):974.

［5］张文超，山世光，张洪明，等.基于局部Gabor变换直方图序列的人脸描述与识别［J］.软件学报，2006，17(12):2508-2517.

［6］朱振峰，卢汉清.基于奇Gabor滤波器与Rayleigh分布的边缘检测［J］.中国图象图形学报，2005，10(7):821-827.

［7］陈小光，封举富.Gabor滤波器的快速实现［J］.自动化学报，2007，33(5):456-461.

［8］程万里，李伟生.基于Gabor-2DLDA方法的人脸识别研究［J］.计算机工程与应用，2008，44(35):179-181.

［9］火元莲，齐永峰.基于Gabor小波与共同向量的人脸识别方法［J］.计算机应用，2009，29(9):2970-2973.

［10］LIU C，WECHSLER H.Independent component analysis of Gabor features for face recognition［J］.IEEE transaction on Neural Networks，2003，14(4):919.