基于改进遗传算法的车间布局重构
2011-01-23唐秋华王雪兰
唐秋华,陈 立,王雪兰
(武汉科技大学机械自动化学院,湖北武汉,430081)
优良的车间布局不仅可以提高生产效率,减少不必要的物流运输,还可以使工作人员在更加安全、健康和舒适的环境中工作。车间布局重构是在现有车间布局基础上,通过局部结构调整,重新理顺车间的工件流、材料流和人流等,特别是优化设备之间的物流运输关系,重新确定其排列顺序和位置,使物流运输逻辑与制造流程一致,从而最大限度地减少运输环节、降低物流运输成本和缩短制造周期[1]。
在车间布局重构时,一般会考虑制造工艺流程、设备类型和数量、可用工作空间、设备几何尺寸以及设备之间的运输频率等影响因素。由于车间布局是多约束多目标的全局优化问题,很难用单一的数值优化模型来描述,导致看似简单的布局设计也往往是NP难问题[2]。
传统的车间布局都是依靠人工设计。根据人工推理的各车间之间、同一车间内各工段之间、同一工段各设备之间的逻辑关联,对车间布局进行模糊规划。受主观经验、自身知识及能力所限,采用该方法很难得到较优解,最多能找到可行解。目前常用的布局方法为系统布局设计(systematic layout planning,SLP)方法,即根据车间内各作业单位间的活动关系密切程度进行布局,借助于图解,将生产单位之间的联系程度定量化,计算出评分值,为平面布局提供依据[3-4]。由于该方法主要是根据两作业单位间的物流当量来指定布局方案,结果虽优于手工布局,但还需要进一步评判。近年来研究人员开始将遗传算法、模拟退火算法和Petri网等应用于车间布局设计。在布局设计中采用模拟退火算法一般仅考虑单一的优化目标函数,最常见的优化准则是最小化设备间的物流耗费[5]。基于Petri网的布局优化方法通常将目标函数放在约束(如位置、距离、路径、邻接关系等)中,寻找一种能满足一系列约束和关系的设计方案,所以其实质是一种多目标准则[6]。
采用遗传算法进行车间布局优化是基于设备间的邻接关系产生空间关系图,并以此作为设计骨架产生布局方案,其具有解集性能优、计算速度快等优点。本文以最小化车间物流总费用为目标,研究基于遗传算法的车间重构策略,对车间设备布局方案进行优化。
1 问题描述
1.1 参数和变量定义
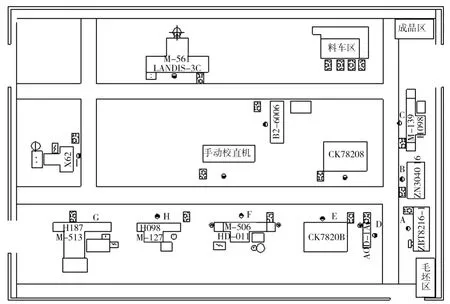
车间布局分为单行布局和多行布局,其中单行布局可看作是多行布局的特例,所以研究车间布局一般都是针对多行布局。在构造车间布局的数学模型之前,要对车间制造系统类型、主要加工对象和产量、现有工艺流程、设备几何尺寸以及使用频次等进行分析,并定义相关参数和变量[7]。图1为车间布局重构示意图,图中所有机器按照相互之间的物流关系,以S形完成多行布置。
定义M台机器构成的集合I={i|i=1,2,…,M},定义这些机器所组成的一种序列J={j|j=1,2,…,M},将这些机器布置在Q行,定义行数集合为N={n|n=1,2,…,Q}。假设mj为布置在第j(j∈J)位的机器,li为机器i(i∈I)的长度,hi为机器i的宽度,dmjmj+1为机器mj与机器mj+1的最小间距,(xi,yi)为机器i的中点坐标为各行间的平均行间距,sn为布置在第n行的机器数,Sn为从第1行至第n行累计的机器数,并令S0=0,L与H分别为车间的长与宽,fii′为机器i(i∈I)到机器i′(i′∈I)之间的往返行程次数,cii′为机器i到机器i′之间往返耗费的单位物流费用,Φ(x)为物流总费用。定义参数G为无穷大。考虑约束情况,引入决策变量vijn,如果机器i位于机器序列的第j位,且机器i位于第n行,则vijn=1,否则vijn=0。
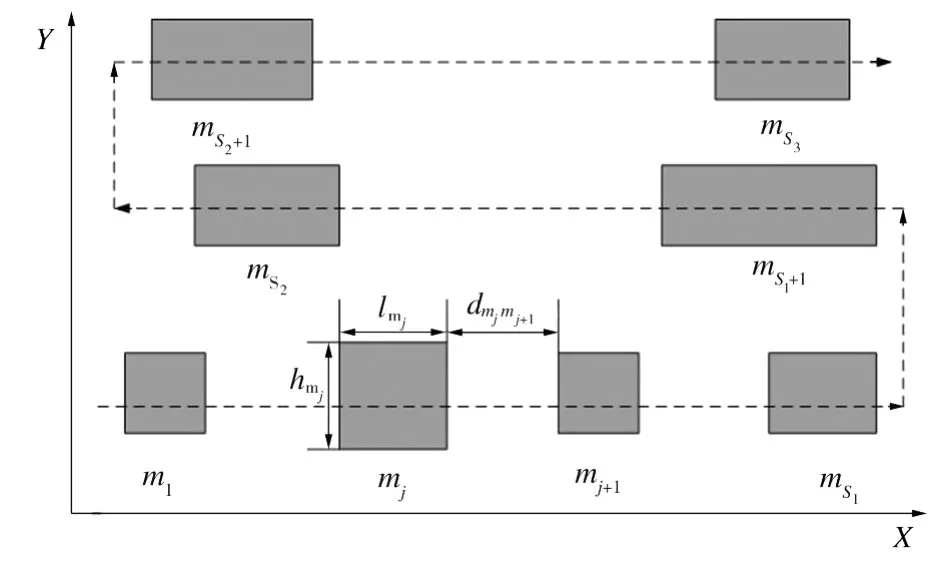
图1 车间布局重构示意图Fig.1 Schematic diagram of workshop reconfiguration
1.2 数学模型
目标函数为
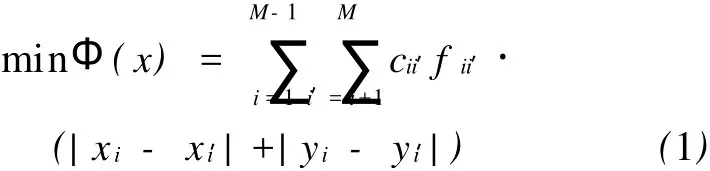
约束条件为
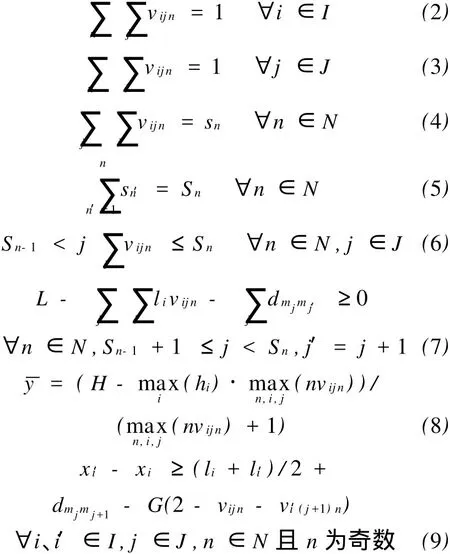
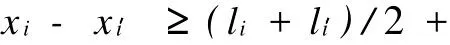
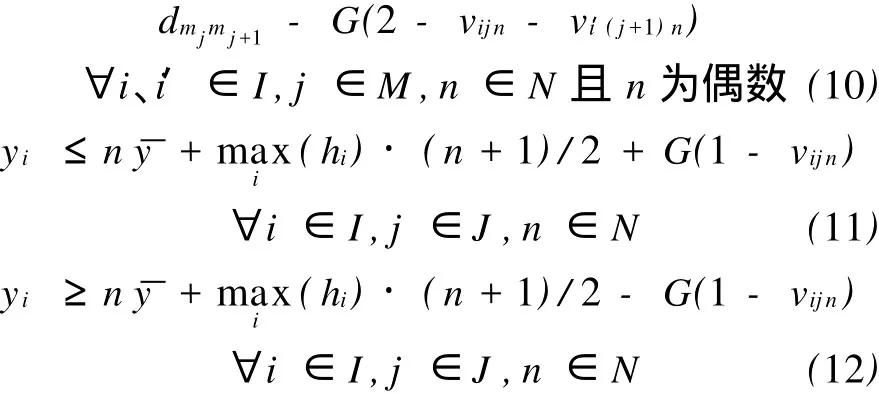
式(1)表示车间布局重构的目标为最小化物流总费用;式(2)限制一台机器只能布置在一行中;式(3)约束在图1所示的机器序列中,每个位置j只能布置一台机器;式(4)和式(5)确定每一行布置的机器数量和累计机器数量;通过界定每行机器的起止顺序,式(6)保证所有机器按线性递增方式排列;式(7)和式(8)确定机器每行之间的平均行间距,同时也确保机器布局的长、宽方向总尺寸不超过限定值;式(9)和式(10)表示位于奇数行的机器x坐标向右按增序排列,而位于偶数行的机器x坐标向左按增序排列,从而保证所有机器按S形布局,同时,式(9)和式(10)要求位于同一行的机器之间满足最小间距约束,以保证其相互之间不出现干涉或重叠;式(11)和式(12)共同保证每台机器的y坐标即为该行坐标。
2 改进的遗传算法
2.1 染色体编码
染色体编码是利用遗传算法求解车间布局重构问题的关键,它不仅影响遗传算子的设计,还决定了搜索空间基因向解空间转换的对应关系[8-9]。对于多行布局,采用一组数字作为行分隔符,表示设备将在几行间进行分配。对于机器排序则采用直接编码的方式。一个染色体的完整编码为{(s1,s2,…,sn,…,sQ),(m1,m2,…,mj,…,mM)},其中,(s1,s2,…,sn,…,sQ)为每行的机器数目;(m1,m2,…,mj,…,mM)为布置在(1,2,…,j,…,M)位置上的机器所构成的序列。该编码中隐含约束关系为:所有机器分配在预先设定的Q行,且
2.2 染色体初始化和适应度函数值
初始种群随机产生。对于每个染色体编码,可以根据式(7)~式(8)确定机器间的最小间距和平均行间距,再根据式(9)~式(12)计算出所有机器的坐标,得到车间实际布局。根据式(1)计算出物流总费用,并以此作为染色体的适应度函数值。
2.3 遗传算子
(1)选择算子。采用常见的排序选择算子产生下一代,同时采用精英策略确保最优个体不被淘汰,这样可以加快算法的收敛速度。
(2)交叉算子。随机选择两个染色体,当且仅当两个染色体的Q值相同时进行交叉,如图2所示。
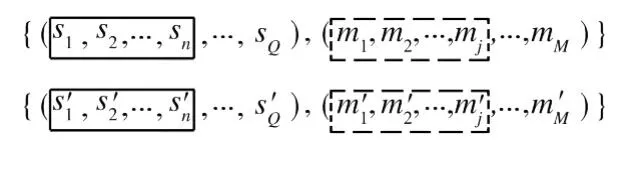
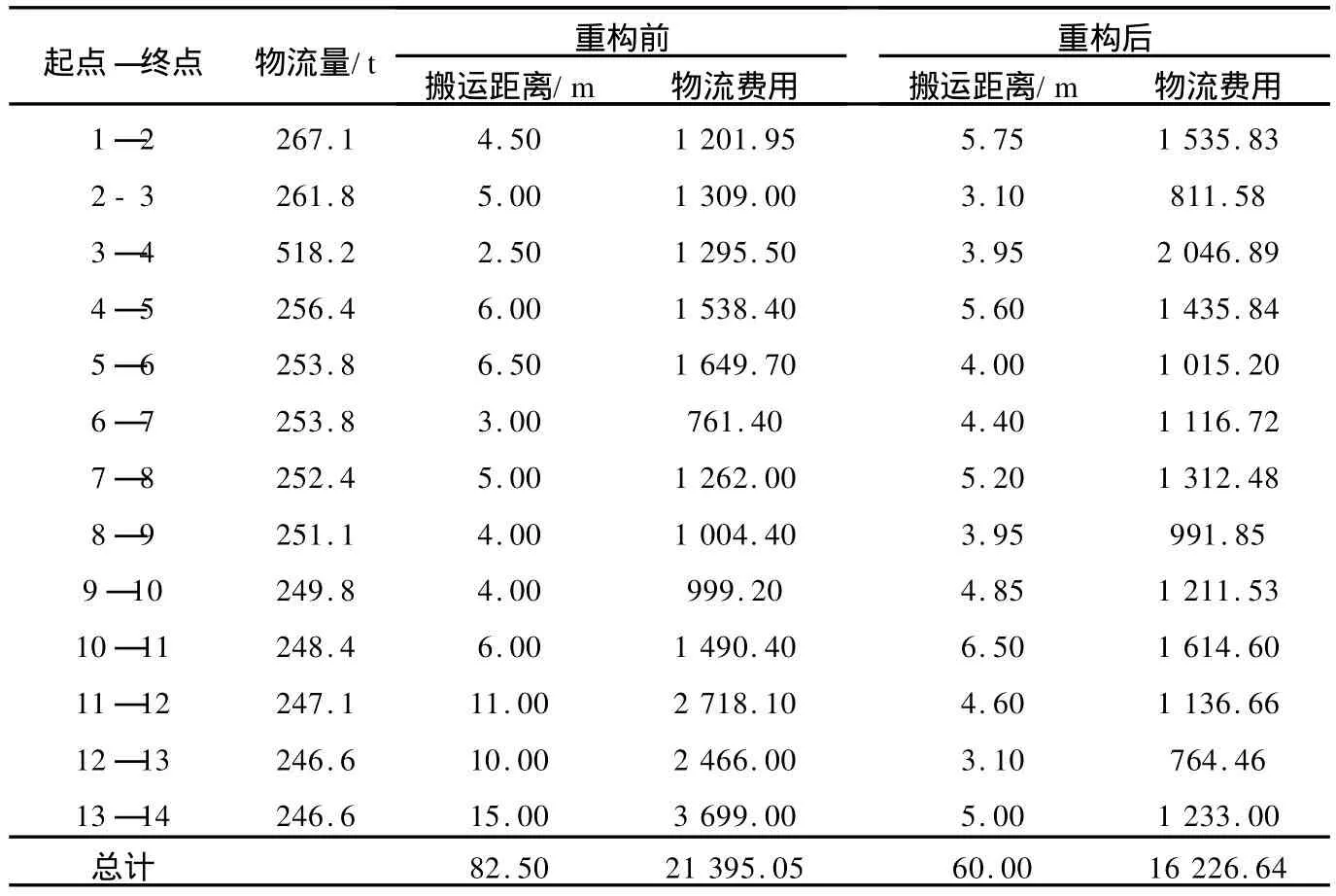
图2 交叉算子Fig.2 Crossover operator
随机选择交叉位n,如果n 步骤1 计算两个染色体前n个片段的机器数量之差Cn。 步骤2 如果Cn=0,则前后片段完整交换;如果Cn>0,则随机选择在+1,…,s′Q)片段中去掉Cn台机器,在(sn,sn+1,…,sQ)片段内增加Cn台机器,然后相互交换;如果Cn<0,则进行与上述相反的操作。 如果n>Q,则限定交叉范围为(m1,m2,…,mj,…,mM),如图2中虚线框所示,即改变机器分配方式。取第一个染色体左边部分,同时在第二个染色体中删除与第一个染色体左边部分相同的基因,剩余的基因按照原来的顺序排列。以第一个染色体左边部分和第二个染色体处理得到的基因为右边部分,重组为一个新的染色体。 (3)变异算子。针对每个染色体,采用两种变异方式。第一种变异是针对各行分配的机器数量,即在染色体的1~N位之间随机选择两个数,其中一个数加1,另一个数减1;第二种变异是针对设备编码序列,即在染色体的N+1~N+M位之间随机选择两个数,相互交换。 某加工车间主要生产3个系列的凸轮轴,3种产品共线生产,主要工艺流程基本相同,如表1所示。车间平面布局如图3所示。 表1 凸轮轴主要加工工序Table 1 Key processes of cam shaft machining 图3 凸轮轴加工车间布局现状Fig.3 Current layout of the cam shaft workshop 结合表1和图3,对车间平面区域进行编码,如表2所示。 根据对生产现场的调研及车间平面编码,绘制如图4所示的车间物流流程图,图中符号内的数字表示区域编码,箭头上的数字表示区域之间单位时间的物流量。图4中的物流流程同时也反映了该凸轮轴车间的工艺路线。 从图4中可以看出,缓存区13存在多个半成品物流汇聚,有可能导致物料混乱,在运送物料到下一个工位之前需要重新审查其类型,给运输增加了不必要的麻烦。同时,车间布局杂乱、空间浪费、物流路线迂回、物流量较大的作业单位距离较远,这都造成了物流成本的增加,而且目前的车间布局不适应多品种小批量生产模式,生产柔性较差。当该车间需要提升产量时,上述问题就变得比较突出,因此不得不耗资进行车间布局重构。 表2 车间平面区域编码Table 2 Codes of the workshop plane 图4 凸轮轴车间物流流程图Fig.4 Logistics flowchart of the cam shaft workshop 为保证物流运输顺畅,提高车间作业效率,拟定以S形混合流水线组织生产,所以车间布局主要考虑生产加工设备的布局,而不考虑暂存区的位置和大小。在车间长度尺寸约束下,两行布局即可完成既定任务,导致最后得到的生产线变成了典型的U形线。布局重构时限定车间可布置长度为25 m,并根据设备尺寸和物流配送等要求,选定行距单元为4 m。首先将表2中{1,7,8,9,10,13,16,17,20,21,24,26,27}在制品库存位置去除,得到表3所示精炼后的车间区域编码。 表3 精炼后的车间区域编码Table 3 Refined codes of the workshop 不考虑表3中毛坯区、成品区位置,于是仅剩下12台机器的布局需要纳入重构范围。提取这12台机器的长、宽、高数据,用矩阵[L,W,H]T表示;并用矩阵表示这12台机器布置时不发生干涉的最小间距。 目前车间主要采用人力运输,根据多耗费的劳动力成本,折算为各机器、库存间的单位物流费用,用矩阵[cmm′]表示。由于全部是人力运输,故可假设矩阵中每个元素都是1。 提取加工每根凸轮轴时物料在各台机器间的往返行程次数,用矩阵[fmm′]表示。 改进遗传算法的参数设为:群体规模Pop=40,遗传代数Gen=100,交叉概率Pc=0.8,变异概率Pw=0.06。计算得到最优个体为{(6,6),(2,3,4,5,6,7,8,9,10,11,12,13)},最小物流费用为16 226.64。重构之后的车间布局如图5所示。车间重构前后的物流费用如表4所示。 从表4中可以看出,车间布局重构后物料搬运总距离减少了22.50m,物流总费用从21 395.05降至16 226.64,减少了5 168.41。 另外,该车间目前采用人工推动料车送料,每车装载20根凸轮轴。根据重构后的车间布局,建议采用传送带送料,这样不但可以减轻工人的劳动强度,还可以提高生产效率。 图5 重构之后的车间布局Fig.5 Reconfigured layout of the workshop 表4 车间重构前后的物流费用对比Table 4 Comparison of logistics costs before and after reconfiguration 合理的车间布局可以减少运输环节,缩短物料运送时间和生产周期,降低生产成本。本文针对设备多行布局,建立了以最小化物流总费用为目标的车间布局重构数学模型,并设计了改进遗传算法进行求解。通过某凸轮轴加工车间布局重构前后物流费用的对比,验证了该模型和算法的有效性。 [1] 蒋祖华.工业工程典型案例分析[M].北京:清华大学出版社,2005:208-215. [2] 唐秋华,肖飞,王雪兰.基于SLP和Flexsim的车间重构研究[J].武汉理工大学学报:交通科学与工程版,2008,32(5):895-898. [3] Ma Zhengyuan.Research on virtual enterprise’s technology fo r supply-oriented system[C]//Proceedings of IE&EM 2001,Tianjin.Beijing:Machinery Industry Press,2001:357-363. [4] 玄光南,程润伟.遗传算法与工程优化[M].北京:科学出版社,2000:124-138. [5] 王金敏,马丰宁,刘黎.模拟退火算法在布局求解中的应用[J].机械设计,2000(2):6-9. [6] 王小娟,钮志强.基于OOPN的港口集装箱堆场作业流程仿真优化研究[J].物流技术,2010(5):48-51. [7] Chase R B,Aquilano N J,Jacobs F R.Operations management for competitive advantage[M].New Yo rk:McGraw-Hill/Irwin,2004:86-97. [8] 王正林,龚纯,何倩.精通MA TLAB科学计算[M].北京:电子工业出版社,2007:360-364. [9] Caruana R A,Schaffer JD.Representation and hidden bias:gray vs.binary coding for genetic algorithm s[C]//Proc 5th Int Conf Machine Learning,Ann Arbor,Michigan.San Fransisco:Morgan Kaufmann Publishers Inc,1988:153-161.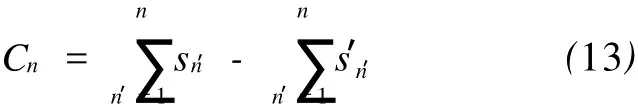
3 实例分析
3.1 某凸轮轴加工车间概况

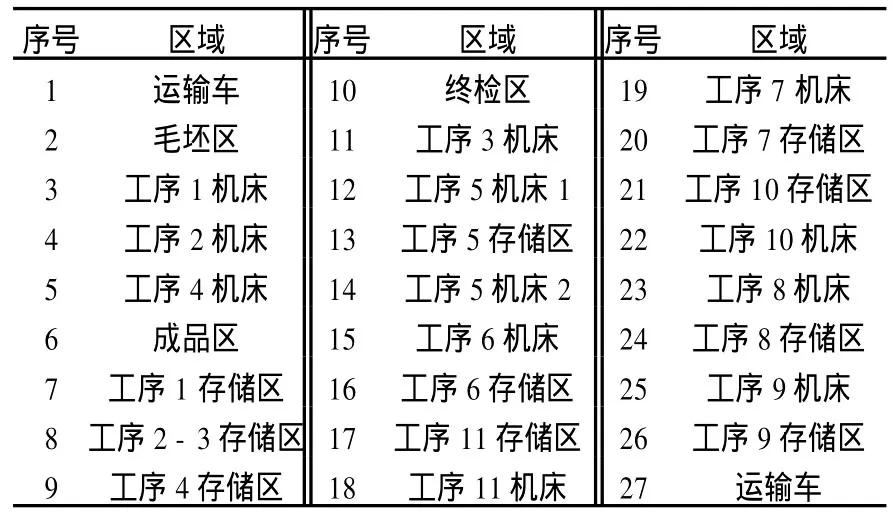
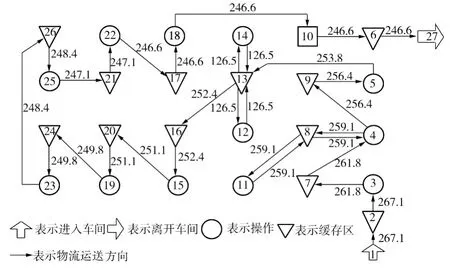
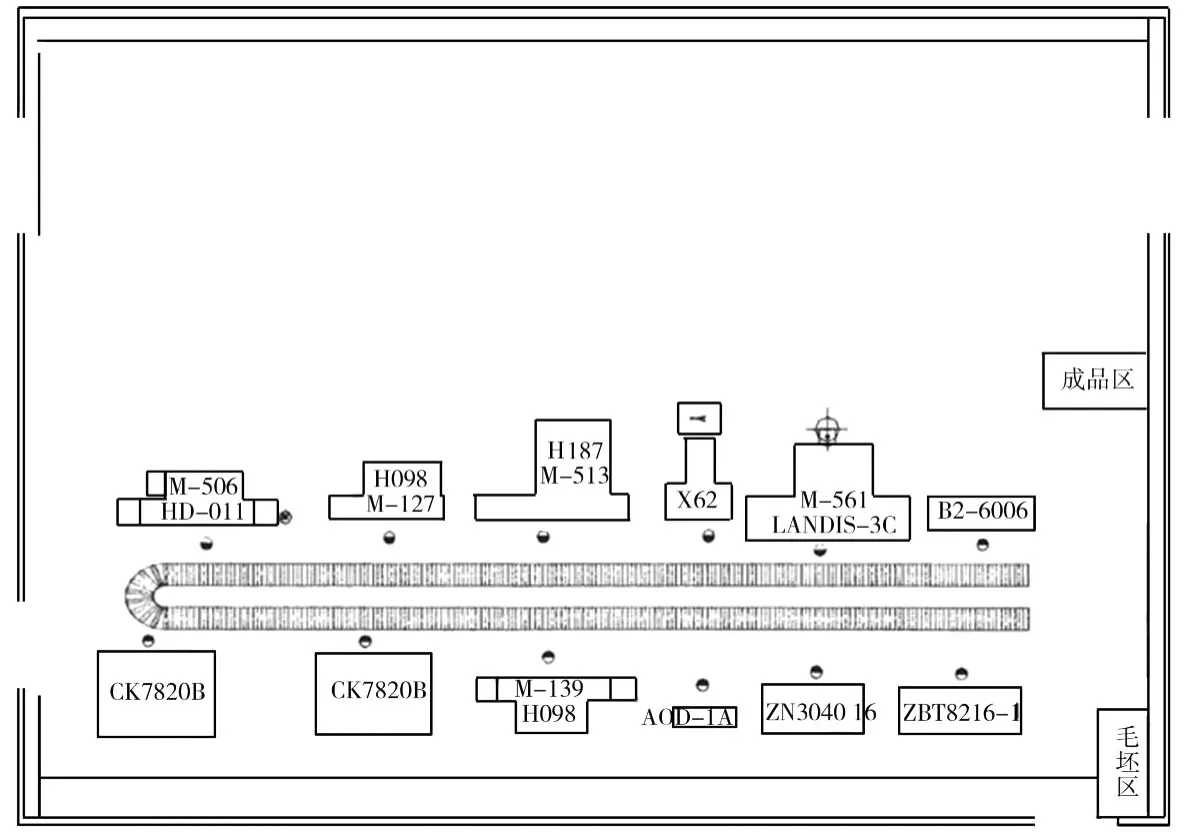
3.2 车间布局重构
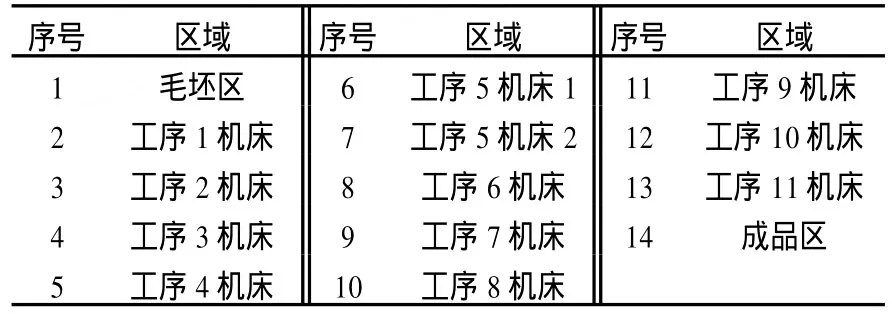


4 结语
