基于最大匹配算法的列车调度模型

孙淑芹,刘家彬,姚 洪

(1.四川民族学院 数学系,四川 康定 626001; 2.四川民族学院 计算机科学系,四川 康定 626001;3.四川师范大学 数学与软件科学学院,四川 成都 610066)

目前,我国铁路大都采用客货混运的机制.在铁路大提速的背景下,需要对重要的铁路干线做出更合理的列车调度方案[1].京沪线是我国最繁忙的铁路线之一,因此本文就京沪全线某一个区间段,如济南至徐州,或南京至上海,在不改变现行列车时刻表的前提下,研究此线最多能安排多少趟次货车,如何制订出具体的列车运行图.列车调度需要遵循一些基本原则[2-6],如:货车运行不能影响客车的运行；运行着的列车之间要有足够的时间间距,等等.京沪铁路线为双线铁路,上行车和下行车之间相互独立,故在此选择下行线进行讨论即可,上行线可类似讨论.为了对行车调度做出详细安排及相关处理,需要了解京沪铁路全部客车的列车时刻表.经过数据采集,得到京沪铁路全部客车的列车时刻表[1].对不再使用的部分列车的数据予以剔除,并选定实际中仍在使用的163辆客车建立京沪铁路客车时刻总表.在实际调度中,不但需要知道每列客车在任意停车站(客车到达且要停车的站)的入站时间及出站时间,还需要知道每列客车经过任意非停车站的路过时间,则在已经建立的京沪铁路客车时刻总表基础上,对每列客车,都利用其运行时的平均速度求出他们经过任意非停车站的路过时间,若有不合理的数据,则进行适当调整,得到京沪铁路客车调度总表.

1 模型假设及符号说明

基于以上分析,现对列车调度做出如下基本假设以及符号说明.

基本条件假设:不考虑货车装卸货物的时间;每个车站停车容量无限制;所有的客车具有相同的行驶能力,所有的货车具有相同的行驶能力.

符号说明:

tc(i,j):第i号客车在第j号车站的进站时间;

to(i,j):第i号客车在第j号车站的出站时间;

tc(k,j):第k号货车在第j号车站的进站时间;

to(k,j):第k号货车在第j号车站的出站时间;

d(m,n):第m号站与第n站之间的距离.

2 模型的建立

在不影响现有的客车运行状态下制定一个合理的货车调度表(即货车时刻表),使得能够运行的货车数量达到最大(即达到最大的运力),并给出相应的列车运行图.

在现实的货车运行中,影响其调度的有以下三方面因素:

首先是货车的空闲时间表,即是在除去现有客车运行时间后的闲置可被利用时间的表格.在现实中,对于货车的安排是建立在不影响现有客车运行的基础上的,所以根据已有的各列客车的列车时刻表统计出可以被利用的空闲时间,所有货车的安排都应该基于此表;其次是当前其他货车运行状态.对于货车的调度还应该遵循不与已安排好的运行货车相冲突的原则.即除了要考虑当前运行在京沪线上的客车,还要考虑正运行在京沪线上的货车,这样才能保证新加入运行的货车和其他列车不构成冲突;最后是货运申请表.货车的调度还取决于当天是否有货运任务,若没有货运任务,则不必安排货车；若有货运任务,则再根据货车的空闲时间表里的空闲时间来安排货车车次.

这三方面因素将共同影响货车的调度,而“货车的空闲时间表”对货车调度起着决定性作用.为了求得一段铁路可以同时通行的货车的理论最大数目,应该先不考虑后两方面因素的影响,即忽略“当前其他货车运行状态”和“货运申请表”对“货车的空闲时间表”的影响.

2.1 基于货车的空闲时间表及货车最大通行量的模型

根据上述分析,取济南到徐州段铁路为例,建立模型.

首先讨论货车的空闲时间表的建立方法.对于连续的两个车站Sj与Sj+1(Sj先于Sj+1),以及相继通过这两个车站的客车ci与ci+1(ci先于ci+1),看是否可以在客车ci与客车ci+1之间插入一列货车gk(或若干列次货车)使得这些列车可以在车站Sj与Sj+1之间安全行驶(即相继两辆列车之间行车时间间隔不得小于行车的安全时间间隔).则至少有以下条件同时成立才能保证列车在车站Sj与车站Sj+1之间的行驶是安全的.(时间单位:分钟)

货车gk从车站Sj出站的时间要至少晚于客车ci一个行车安全时间间隔Ts∶to(k,j)-Ts≥to(i,j);

货车gk从车站Sj出站的时间要至少早于客车ci+1一个行车安全时间间隔Ts∶to(k,j)+Ts≤to(i+1,j);

货车gk到达车站Sj+1的进站时间要至少晚于客车ci一个行车安全时间间隔Ts∶tc(k,j+1)≥tc(i,j+1)+Ts;

货车gk到达车站Sj+1的进站时间要至少早于客车ci+1一个行车安全时间间隔Ts∶tc(k,j+1)≤tc(i+1,j+1)-Ts;

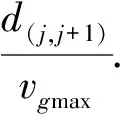
若以上条件不能同时满足,则客车ci与客车ci+1在车站Sj与Sj+1之间的行驶阶段是不能插入货车运行的；否则,可以对于车站Sj求出一个空闲时间段△tvacancy∶△tvacancy=max(to(k,j))-min(to(k,j)).

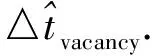
显然,客车ci与ci+1的选取对车站sj的一个“可行的空闲时间段”的计算有决定性作用.由于经过每一个车站的客车都有若干辆,那么,对于每一个车站,都将有若干个可行的空闲时间段和到达下站的到达时间范围,而所有车站的可行的空闲时间段和到达下站的到达时间范围就构成了整张“货车的空闲时间表”.这就是构造货车的空闲时间表的不等式组模型.从而求得济南到徐州铁路段理论上最大的货车通行量Ngmax.

其中,wj表示第j号车站拥有的可行的空闲时间段的个数；△tvacancy(j,l)表示第j号车站的第l号可行的空闲时间段.Ngmax表示济南到徐州货车数目的瓶颈量.

2.2 列车时刻表的构造算法

根据已经求得的货车的空闲时间表和货车的最大通行量,基于原则:对于任意车站,先进站的货车,先出站,即先进先出.设计如下算法,构造在理论上达到最大货车行车数量时,货车时刻表的一个可行解,进而再制定列车运行图.

称货车的空闲时间表最大匹配算法(VacancyMaximumMatchingAlgorithm)为VMM算法.VMM算法的结果是以一张时刻表VMMGrid来表现,形如表1.

表1 VMMGrid示例表

下面详细叙述VMM算法:

step1:做一个空表格VMMGrid,其行数VMMGrid.Lines.Count=济南与徐州之间的车站数目=8；其列数VMMGrid.Columns.Count=济南到徐州理论上最大的货车通行量Ngmax×2+1.置单元VMMGrid.Cells[0,0]为空；把首行VMMGrid.Lines[0]除去VMMGrid.Cells[0,0]后的每两格为一组合并,然后置入站标Sj(j=0,…,6)(S7不置入是因为S6中的“到下站时刻”就确定了S7的数据)；把首列VMMGrid.Columns[0]除去VMMGrid.Cells[0,0]后的每格依次置入货车gk(k=1,…,Ngmax).这样便形成了VMMGrid的框架,如上述VMMGrid示例表.

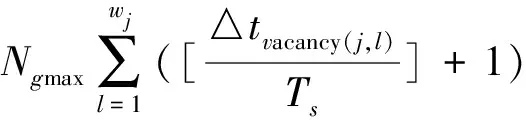
step4:求Sj0到Sj0之后的所有车站的可行的空闲时刻.

step4.1:求Sj0到Sj0+1可行的空闲时刻.

step4.2:若Sj0的所有可行的空闲时间段已经都处理了,则转step4.5,否则取下一个没有处理的空闲时间段,记此空闲时间段段首时间点为初始时间点,记为t0;

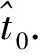
step4.4:若t0+Ts属于当前可行的空闲时间段,那么令t0∶=t0+Ts,转step4.3,否则转step4.2；

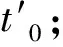
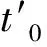
step4.9:从Sj0+1所有可行的空闲时间段的处理成的所有时间点中除去已经置入VMMGrid的点后,再作加24小时处理,并重新都视为未处理过,转4.6

step4.10:若S6被处理过了,转step4.11,否则令Sj0∶=Sj0+1、Sj0+1∶=Sj0+2,转step4.1；

step4.11:Sj0到sj0之后的所有车站的可行的列车行车时刻建立完毕,退出step4.

step5:求Sj0之前所有车站的可行的列车行车时刻.(与step4的执行流程相类似,逐渐对比Sj0与Sj0-1直到S1被处理完.其中主键选为VMMGrid.Columns[2j0+1],初始时间点选取顺序变为由后向前,匹配规则也与step4中相反.)

step6:算法结束,退出.

VMM算法中的step4和step5为算法的主要执行模块,现以step4为例,建立主算法模块流程图,如图1所示:

图1 VMM主算法模块

根据VMM算法得到的VMMGri即可做出列车运行图.

3 模型求解及结果分析

3.1 货车的空闲时间表和货车最大通行量的模型结果

根据上述货车的空闲时间表模型和货车最大通行量的模型,并以货车运行时的平均速度为60千米/小时,求得货车的空闲时间表,取其中的一部分作为示例显示如表2.

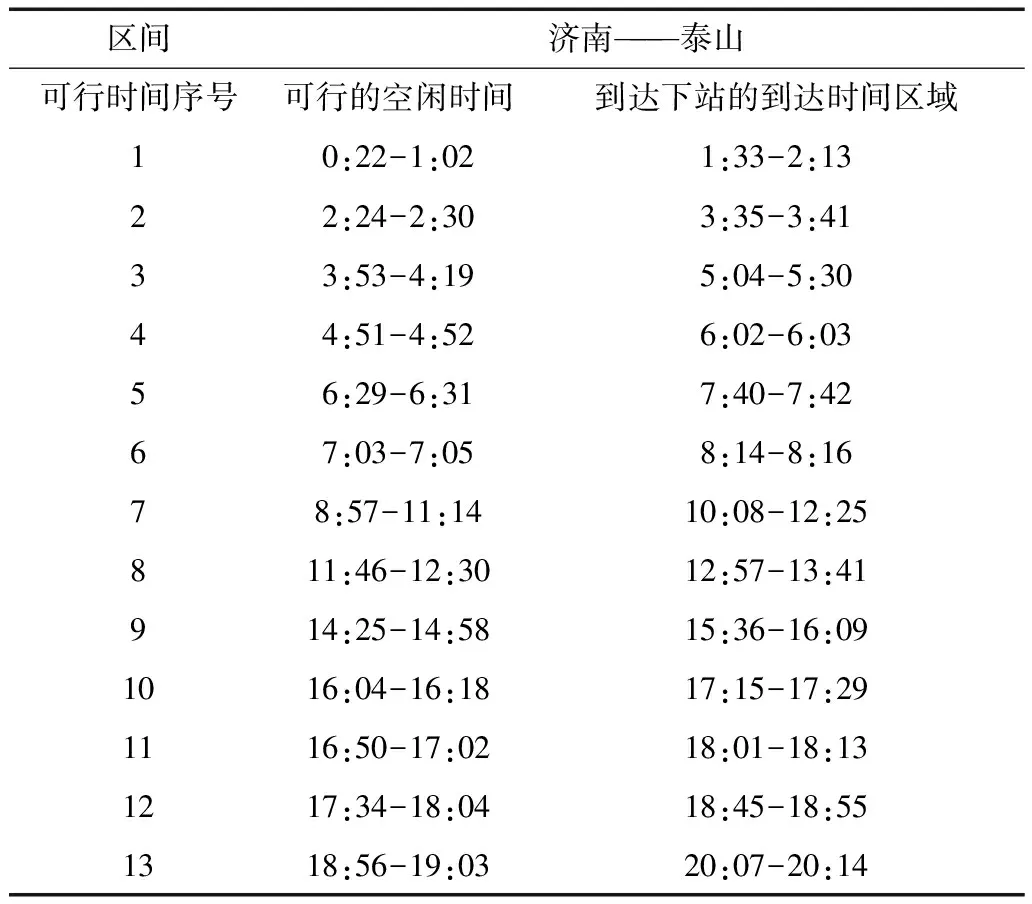
表2 货车的空闲时间表详表节选表

可以看出,货车的空闲时间表清楚地反映了两个车站之间可以发出货车的时间段以及在这个时间段发车后到达下一站的时间段.

根据货车运行速度的不同,得到的货车最大通行量也不同,其结果如图2所示:

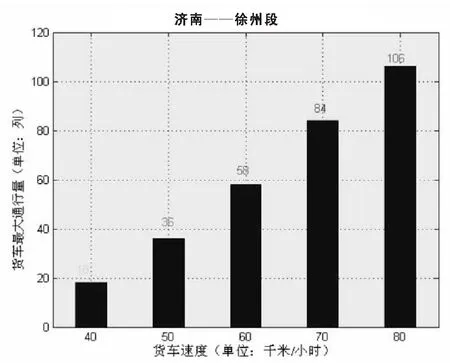
图2 货车最大通行量与速度关系图

此表清楚地反映了随着运行的货车速度不同,铁路段所能允许同时通行的货车数量也不同,在一定范围内货车最大通行量随着货车速度的提升而增大.

3.2 列车运行图的构造算法结果及分析

在此VMM算法中,取货车运行时的平均速度为60千米/小时,进行计算,得到VMMGrid,再从VMMGrid制定出的列车运行图总图.从VMMGrid的内容看出,它详细指明了各个货车在每个车站的到站时间,是否停车,停车多久以及何时开车这些关键数据.列车运行图总图意义则在于,可以根据实际需要选取那些合适的货车车次运行于实际中,而其他的车次可以作为备用；从这张图表看出所有的线路无交叉,这就直观的说明了使用VMM算法得到的货车时刻表是可行的,进一步体现了VMM算法的可行性.

此外,需要注意,在实际的货车运行当中,还应该尽量遵循下列规则:

1)有直达货车,也有非直达货车:直达货车保证了运送货物的实时性；非直达货车则保证了每个车站有货运请求时都可以得到满足.

2)各列货车之间有一定的运行时间间隔:这给以后的列车调度提供了更加宽松的环境,尤其是在客运高峰期,为临时列车的加开提供了基础；在某列车晚点时提供了可以实时调整的空间.

3)有限的等待时间:列车到站后不能无限制的等待,等待时间有上限.

4)其他特殊需求:如某城市为货运大城,则使在此站停车的货车数量相对较多,等等.

根据实际中存在的约束,从列车运行图总图中,选择满足这些条件的10趟车次,用于实际调度中,如图3.

图3 部分列车运行图

从此图中可以看出:有从济南直达徐州的货车,也有在各站停靠的货车；每列货车之间都有比较合理的运行时间间隔,这是满足实际需要的.

综上所述:以货车的空闲时间表为基础,根据VMM算法,可以生成可行的详细货车时刻表及满足实际需要列车运行图.

4 模型评价及改进

(1)数据处理中的一些问题.在本模型数据处理阶段,是采用列车平均速度计算出客车在各非停车站的到站时间,这种处理方式比较简洁,在一定程度上是可行的,但如果能采集到实际的数据将是最准确的处理方式.

这是可以改进的地方,只需采用实际数据就可以使基于此数据得到的结果更准确合理.但这并不影响问题的处理方法,本题中的解决方案依然可行.

(2)关于VMM算法.VMM算法是实现构造时刻表的一种有效可行的算法,其主要模块在step4中完成,其关键可以概述为从到站时刻寻找一个最近的可用空闲时刻作为发车时间.这样会产生一个问题:若列车到站时间相对较晚,则在此站的某些可用的空闲时间会被错过,造成此列车将等待更长时间(直到第二天可用的空闲时刻),而这种处理方法却能保证绝大多数货车找到最近的可用空闲时刻,从而使他们的效率达到最大.可以说这是牺牲了某列或某几列货车的效率来保证其他货车的效率达到最大.

另一种处理方法是,当确定某列货车会出现长时间等待的情况时,重新对此车站所有货车的发车时刻统一做出调整,使得所有货车的平均等待时间达到最小.

在实际中,这种长时间等待的情况出现的可能性较小,如本题中的济南到徐州段就没有这种长时间等待的情况；又考虑到货车运输对实时性的要求并不高,故算法中采用第一种方法来处理长时间等待的情况,即使有对实时性要求高的货车,也可以保证不牺牲它的效率.

[1]全国大学生数学建模竞赛组委会.数学建模的实践[M].北京:高等教育出版社,2007.

[2]聂磊,张星臣,赵鹏,等.高速铁路列车运行调整策略的研究[J].铁道学报,2001(4):1-6.

[3]兰淑梅.京沪高速铁路客车开行方案有关问题的研究[J].铁道运输与经济,2002(5):32-35.

[4]赵丽珍,朱家荷.利用区间渡线组织列车越行对高速铁路区间通过能力的影响[J].中国铁道科学,2002(5):11-17.

[5]罗晴,金福才,胡思继.列车运行调整问题的分解协调计算模型[J].北京交通大学学报,2004(6):87-89.

[6]赵强.列车运行方案车站到发线需求可行性模型及其算法[J].西南交通大学学报,2000(2):196-200.