运用匈牙利法求解分配问题
2011-01-23于淑兰
于淑兰
(泊头职业学院 经济管理系,河北 泊头 062150)
匈牙利法是求解极小型(优化方向为极小)指派问题的一种方法,这种方法最初由w.w.kuhn提出,后经改进而形成,解法基于匈牙利数学家D.König给出的一个定理而得名.它的基本原理是:对任何一个求最小值的效率矩阵(cij),将其某一行或某一列的各个元素减去或者加上同一个常数k,得到一个新的矩阵(bij),则新矩阵与原矩阵有相同的最优解.如果问题是求最大值的话,则需要把目标函数转换成求最小值,再使用匈牙利法求解.当矩阵中独立零元素的个数等于矩阵阶数n时,独立零元素对应的变量xij=1,其他元素对应的变量xij=0,这就是分派问题的最优解矩阵,而很多情况下我们很难直接得到独立零元素的个数等于矩阵阶数这种结果,遇到这种情况需要进行调整,在《运筹学基础及应用》这本教材中给出了调整的方法,在教学过程中发现书中针对此内容写的有些松散,方法不易学生接受,难度大.结合自己的教学经验,归纳整理了一个更为简单可行的调整方法.下面将其应用到具体实例中加以说明.
例1 有一份说明书,要分别译成英、日、德、俄四种文字,交甲、乙、丙、丁四个人去完成.因个人专长不同,他们完成翻译不同文字所需的时间(h)如表1所示,应如何分配,使这四人分别完成这四项任务总的时间为最小.
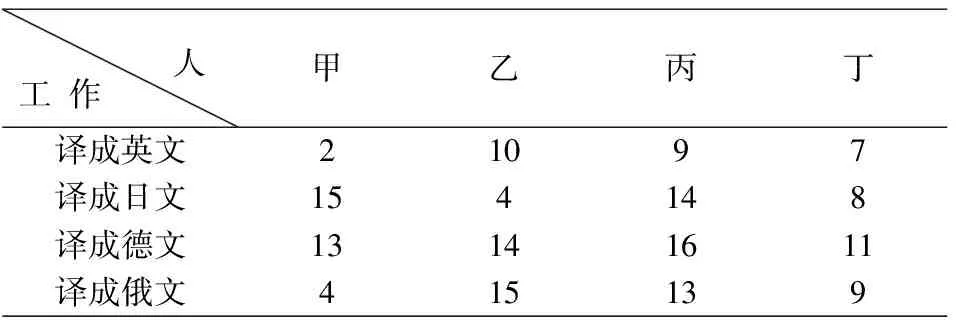
表1 翻译不同文字所需的时间(h)
解题步骤如下:(1)先从效率矩阵的每行减去该行的最小元素,再从效率矩阵的每列减去该列的最小元素;(2)找出矩阵中独立零元素.先找出每行中仅有一个“0”的元素,并划去与该“0”同列的其他0元素,即φ;然后对矩阵的列作同样的变换;(3)当矩阵中独立零元素的个数等于矩阵的阶数时,可以分派任务,否则需要调整矩阵,方法如下:①对没有独立的零所在的行打*;②在已打*的行中,对φ所在的列打*;③在已打*的列中,对有独立零所在的行打*;简记为:没有零的行→φ的列→有独立零的行;④重复以上三步直到不能做标记为止;⑤用直线划去没有标记的行,划去有标记的列;⑥将保留下来的元素减去它们的最小元素,将仅被一条直线覆盖的元素保持不变,将同时被两条直线覆盖的元素,分别加上“减去的最小元素”.
调整完毕后,再重新找出独立的零元,满足独立零元的个数等于矩阵的阶数,就停止,否则就按上述步骤继续调整,直到得到分配方案为止.
解 (1)从矩阵的每行减去该行的最小元素,再从矩阵的每列减去该列的最小元素(目的是为了简化数据);

(2)找出矩阵中独立的零元素,记得要划去对应列或者对应行的“0”;

(3)由于独立零元素的个数为3个,小于矩阵的阶数4,所以必须进行调整.

未被直线覆盖的数字最小的是2,将“8、2、5、11、4、5”分别减去2,将同时被两条直线覆盖的数字“11、2”加上2,得到新的矩阵,并找出独立的零元

即最优方案为:甲将说明书译成俄文,乙将说明书译成日文,丙将说明书译成英文,丁将说明书译成德文,全部所需的时间为4+4+9+11=28h,这种方法,相对于教材要简单明了,思路上更清晰,学生更容易接受.
有时我们会发现对矩阵进行调整后,各行各列都没有独立的零元素,对于这种情况就需要进行假设.
例2 假定有五位司机被分配完成五项任务,完成各项任务的时间(h)如表2:问应如何分配,使得这五位司机完成这五项任务时间最短.
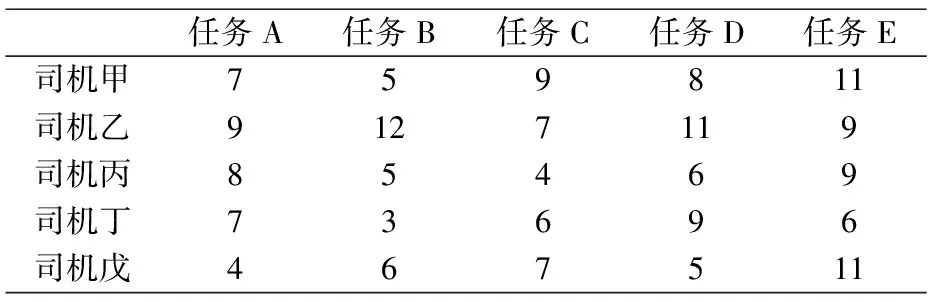
表2 司机完成任务的时间
解 (1)从矩阵的每行减去该行的最小元素,再从矩阵的每列减去该列的最小元素,并找出独立的零元素.


(2)调整矩阵


独立零元的个数不等于矩阵的阶数,仍需要调整.
(3)按照规则进行调整
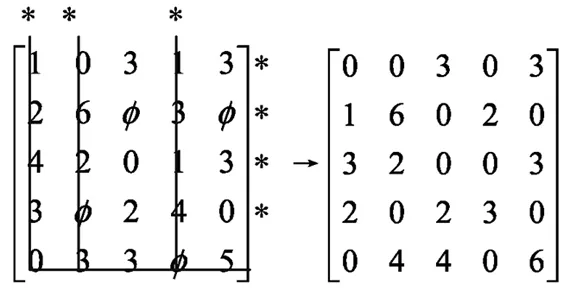
矩阵中各行各列都没有独立的零.可以从第一行中任意一个“0”处进行假设,此例中第一行共有三个零,可以进行三种假设.
(4)①假设司机甲做任务A,找出独立的零元,要注意的是,甲已经做了任务A,就不能再做其他任务,所以第一行中余下的两个“0”应划去,同时划去第一列的“0”;再从各行到各列找出独立的零元.

独立零元的个数等于矩阵的阶数,得到分配方案1.
司机甲完成任务A,司机乙完成任务E,司机丙完成任务C,司机丁完成任务B,司机戊完成任务D.完成该方案总的时间为:7+9+4+3+5=28h.
5+7+6+6+4=28h.
5+7+6+6+4=28h.
经过对比发现三个方案用时是一样的,所以用哪个方案均可,如果问题中三个方案的时间不相同,我们应该取用时最短的那个方案.
参考文献:
[1]王凯阳.物流运筹学[M].北京:北京大学出版社,2009.
[2]胡运权,等.运筹学基础及应用[M].第五版,北京:高等教育出版社,2008.
