自升式平台举升状态运动响应试验研究＊

勾 莹 沈 洁 滕 斌 侯金林 谭 越 郭士勇 丛培文

（1.大连理工大学海岸和近海工程国家重点实验室； 2.中海油研究总院）

自升式平台举升状态运动响应试验研究＊

勾 莹1沈 洁1滕 斌1侯金林2谭 越2郭士勇1丛培文1

（1.大连理工大学海岸和近海工程国家重点实验室； 2.中海油研究总院）

对自升式平台处于举升状态桩腿下放和提升过程时的运动响应进行了物理模型试验研究。针对目标海域实际海况分别研究了不同有效波高和波浪入射角度对平台运动响应的影响，所得结果可为自升式平台设计提供依据。

自升式平台 举升 运动响应 模型试验

自升式平台通过液压步进式升降装置实现升降功能。当自升式平台处于举升状态桩腿下放和提升过程时，平台主体受到波浪的载荷较大，平台运动响应也较大，但目前针对自升式平台举升状态运动响应特性的研究还很少。为了为自升式平台设计提供依据，利用大连理工大学海岸和近海工程国家重点实验室的非线性波流水槽对某自升式平台运动响应进行了物理模型试验研究。该自升式平台为钢质非自航平台，适用于北部湾或渤海湾40 m以下水深水域，具有原油生产、处理、储存和外输能力，能提供40人的生活和居住条件。大连理工大学海岸和近海工程国家重点实验室的非线性波流水槽长55 m，宽4 m，水深2.4 m；水槽一端安装有微机控制的造波机，用于产生不规则波浪；水槽设有2台流量1.0 m3/s轴流泵的造流系统，配有数据自动采集系统。

1 自升式平台举升状态运动响应试验

1.1 平台模型主要参数

在自升式平台运动响应试验中，模型与实型之间须满足几何相似、静力相似和水动力相似条件[1]。对于几何相似，实型与模型的几何尺寸应满足

式（1）中：L为特征线尺度；下标s代表实型量，m代表模型量；λ为缩尺比。对于静力相似，要满足模型平台和实际平台的重心、转动惯量等相似。在水动力方面，须满足实型和模型之间的重力相似，即满足傅汝德数和斯托哈数相等，因此有

式（2）中：V为速度；g为重力加速度。

根据上述相似法则，得出模型与实型各物理量之间的转换关系（表1）。目标平台的随体坐标定义如图1所示，X轴与Y轴交于平台主体的几何中心，Z轴竖直向上，0点位于平台主体结构底部，平台重心坐标为（2.96，0，0.26）。平台所在位置实际水深40 m，水面在平台底部以上3 m。桩腿距海底25 m，距离平台底部12 m。

表1 模型与实型各物理量之间的转换关系

图1 目标平台平面示意图

综合考虑平台尺度及试验水槽宽度，选定平台实型与模型之间的缩尺比为λ＝45，按照表1的转换关系得到平台模型的主要参数，见表2。

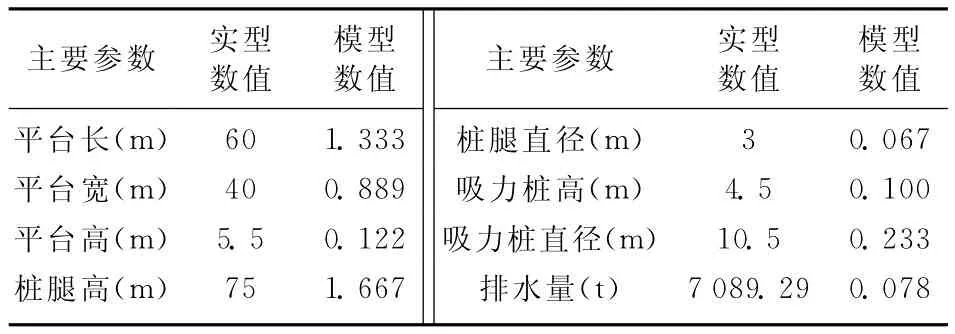
表2 平台实型与模型主要参数值

1.2 试验环境要素

根据目标海域的实际情况，试验主要分为两部分：一是研究有效波高对平台运动响应的影响，试验中波浪入射角度为180°，不规则波的有效波高分别为2.5、3.0、3.5和4.0 m，各不规则波的平均跨零周期分别为5.0、5.0、6.0和7.0 s；二是研究波浪入射角度对平台运动响应的影响，试验中不规则波的有效波高为2.5 m，波浪入射角度为180°、90°和34°。在试验过程中，海流速度为1.12 m/s，风速为20 m/s，海流、风的方向与波浪同向。

根据目标海域的实际海况，不规则波波谱选用Jonswap谱，即

其中

式（3）中：TP为谱峰周期，s；γ为谱峰升高因子，取为3.3；H1/3为有效波高，m；f 为波浪频率，Hz；TH1/3为有效波周期，s；fP为谱峰频率，Hz。

1.3 平台模型布置方式

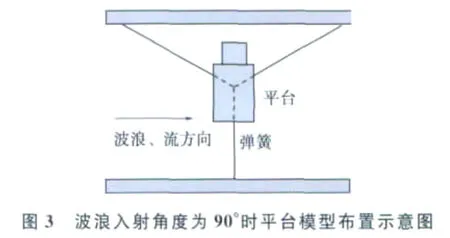
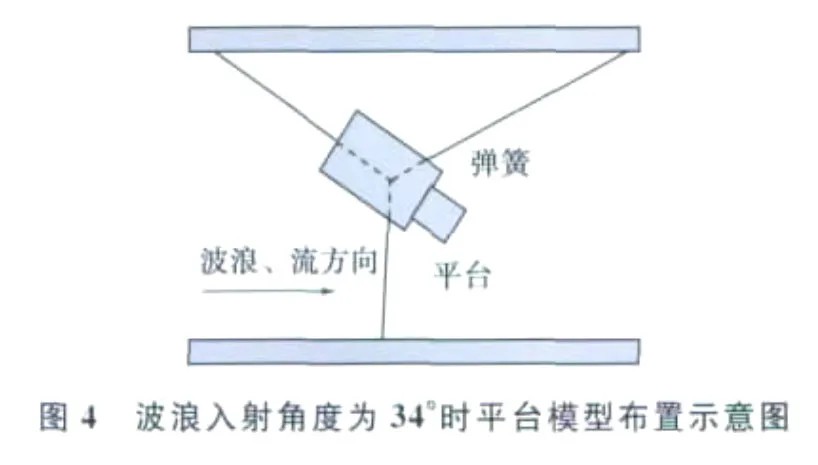
试验在水槽中进行，采取调整平台角度的方法模拟不同的波浪方向。波浪入射角度为180°时的平台模型布置方式如图2所示，平台模型通过一水平弹簧系泊在水槽中央的固定点处，平台模型上装有无触点六分量仪以记录平台的运动响应，弹簧上连接传感器记录弹簧的水平拉力。波浪入射角度为90°和34°时平台模型布置方式分别示于图3和图4，这2种情况平台模型均采用3根弹簧系泊。

2 试验结果及分析

为保证实验结果的可重复性，对于每个实验组次都进行了3次重复实验，根据各波浪的平均跨零周期，换算出实验波列的平均跨零周期小于1.04 s，由此得出每组实验采样时间应不少于104 s，以保证不规则波列至少包含100个波。在试验中，采样时间均选为150 s。

对于入射角度为180°的风、浪、流环境载荷，平台运动响应主要为沿X轴方向（平台长度方向）的纵荡位移、沿Z轴方向的升沉位移和绕Y轴（平台宽度方向）的纵摇角位移，另外3个自由度的运动响应很小。图5～7分别是有效波高为2.5 m时平台纵荡位移、升沉位移和纵摇角位移的时间历程。

还分别进行了不规则波波浪入射角度为180°、有效波高分别为3.0、3.5和4.0 m的平台运动响应试验，并对试验结果进行了统计分析，采用上跨零点法得出了运动响应的最大值和1/3有效值，根据表1换算成为实际平台的运动响应，见表3。

表3 波浪入射角度为180°时不同有效波高条件下实际平台运动响应统计结果

从表3可以看出，随着有效波高的增加，纵荡位移、升沉位移和纵摇角位移的幅值都在增加；当有效波高为4.0 m时，纵荡位移达到最大值为3.52 m，升沉位移达到最大值为2.57 m，纵摇角位移也达到最大值为7.3°。根据自升式平台运动响应试验结果，并从工程安全考虑，自升式平台的安全作业环境应该在波浪有效波高小于3.0 m的范围内。

为了研究不同波浪入射角度情况下平台的运动响应，又分别进行了不规则波波浪入射角度为90°和34°时平台运动响应试验（不规则波波高都为2.5 m，平均跨零周期为5.0 s），其统计结果见表4。

表4 波浪入射角为180°、90°、34°不规则波有效波高2.5 m条件下平台运动响应结果

从表4可以看出：当波浪入射角度为90°时，平台水平位移最大，为1.36 m，1/3有效值为0.73 m，升沉位移也最大，为0.83 m，1/3有效值为0.46 m；这是因为波浪入射角度为90°时平台迎浪面积较大，因此波浪荷载也较大，以至产生了较大的平动位移。

当波浪入射角度为34°时，平台纵摇最大，为3.84°，1/3有效值为2.01°，这是因为入射角度为34°时平台的重心并不在平台的几何中心上，平台重心沿平台长度方向有一定的偏心距，使得平台甲板上浪明显，而在波浪作用下，平台会产生较大的纵摇运动响应。因此，为了防止因平台重心偏心较大引起的纵摇运动，在设计时应考虑通过调整配载适当减小平台的偏心。

3 结论

对自升式平台举升状态运动响应进行了物理模型试验，试验结果分析表明，在自升式平台设计时，平台的安全作业环境应在波浪有效波高小于3.0 m的范围内；为了防止因平台重心偏心较大产生的纵摇，应该考虑通过调整配载适当减小平台的偏心。

[1] 中华人民共和国交通部.JTJ/T 234－2001波浪模型试验规程[S].北京：人民交通出版社，2001.

An experiment study on jack up platform motion in lift up state

Gou Ying1Shen Jie1Teng Bin1Hou Jinlin2Tan Yue2Guo Shiyong1Cong Peiwen1
（1.State Key Laboratory of Costal and Offshore Engineering，Dalian University of Technology，Liaoning，116085；2.CNOOC Research Institute，Beijing，100027）

The motion of jack up platform during rising or sinking process in lift up state is studied by model experiment method.To examine the effects of significant wave height and incident wave direction on platform motion，a series of experiment tests are carried out with different sea states.The results are significant for designing jack up platform.

jack up platform；lift up state；motion；model experiment

＊中国海洋石油总公司综合科研课题“可移动式自安装平台关键技术研究”部分研究成果。

勾莹，女，2006年毕业于大连理工大学港口海岸及近海工程专业，获博士学位，现主要从事波浪与海洋结构相互作用方面的研究。地址：辽宁省大连市大连理工大学海岸和近海工程国家重点实验室（邮编：116085）。E－mail：gouying＠dlut.edu.cn。

2010－09－13改回日期：2010－11－07

（编辑：夏立军）