一类高阶的差分方程解的稳定性

葛琦，侯成敏

（延边大学理学院 数学系，吉林 延吉133002）

一类高阶的差分方程解的稳定性

葛琦，侯成敏

（延边大学理学院 数学系，吉林 延吉133002）

研究了非线性差分方程其中k∈ ｛2，3，…｝，fg是［0，＋ ∞）上连续非负递增函数.证明了方程在初始条件（x0，x1，…，xk－1）∈Rk＋下的解是稳定的，并且当k为偶数时，收敛到（a0，a1，…，ak－1）的解的初始点的集合是形如（y0，y1，…，yk－1）∈ ［a0，＋ ∞）× ［a1，＋ ∞）× … ×［ak－1，＋ ∞）的点的集合，其中ai≥0（i＝0，1，…，k－1），同时存在唯一连续增函数hi∶［ai，＋∞）→ ［ai－1，＋ ∞），使hi（yi）＝yi－1（i＝1，3，…，k－1）.

差分方程；收敛性；稳定性

0 引言

本文受文献［1］和［2］的启发，研究了非线性差分方程

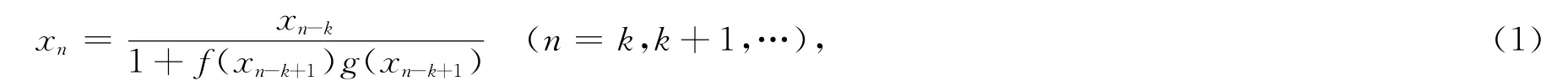
其中k∈｛2，3，…｝，fg是［0，＋∞）上连续非负递增函数．根据差分方程的实际意义，我们假设本文中的初始条件是非负的，对应初始条件的解称为源于Rk＋的，其中R＋表示区间［0，＋∞）．本文记Z＋＝｛1，2，…｝，Z＊＝ ｛0，1，2，…｝．

1 主要结果

定理1 令f是［0，＋∞）上连续非负递增函数，且存在常数ξ，c，L＞0，使得f（x）≤cxL，x∈［0，ξ）．现设和为差分方程

源于Rk＋的2个解，则如果对任意给定的ε＞0，存在δ＞0，使得成立，那么有

以下分2种情况讨论：

情况1 k为偶数．i）考虑xnk＋j→0，xnk＋j＋1→aj＋1的情形，其中aj＋1＞0（j＝0，2，…，k－2）．先考虑有限项．给定ε＞0，且，选择充分大的N∈Z＊，使得对任意的n≥N有

现假设（ynk，ynk＋1，ynk＋2，…，ynk＋k－1）→ （b0，b1，b2…，bk－1）．由于a3＞0，所以有b3＞0．通过归纳可以证明

由（7）和（8）式及a1－2ε＜ykN＋1，得yk（N＋m）＋1≥ykN＋1·exp｛－c2εL｝≥ （a1－2ε）（1－c2εL），由此推得（5）式成立．综上所述可知成立．同理可证明n≥N）成立．

ii）考虑xnk＋j→aj，xnk＋j＋1→0的情形，其中aj＞0，j＝0，2，…，k－2．由于证明过程与i）类似，故省略．

iii）考虑xnk＋i→0的情形，其中i＝0，1，…，k－1．这里只证明存在N∈Z＊，使得n＞N，其他情况类似．对于任意给定的ε＞0，取充分大的N∈Z＊，使xkN＜ε，因为x｛｝nk关于n递减，所以对于所有n≥N有0＜xkn＜ε．要想证明，只需证明－2ε＜ykn＜2ε（n＞N），即只需证ykn＜2ε（n＞N）．与i）中讨论类似，可知又由于y｛｝nk关于n递减，所以对任意的n＞N有ykn＜ykN＜ε＋xkN＜2ε．因此成立．

iv）证明当k是偶数时，有且只有以上3种情况，其他的情况均不合理．

若xkn＋k－1→ak－1＞0，则由方程（2）必有，下证

事实上，由于xnk＋（k－2）→0，所以对任意充分小的ε＞0，存在充分大的N∈Z＊，使得当n≥N时有xnk＋（k－2）＜ε.类似于（6）和（7）式的证明可得

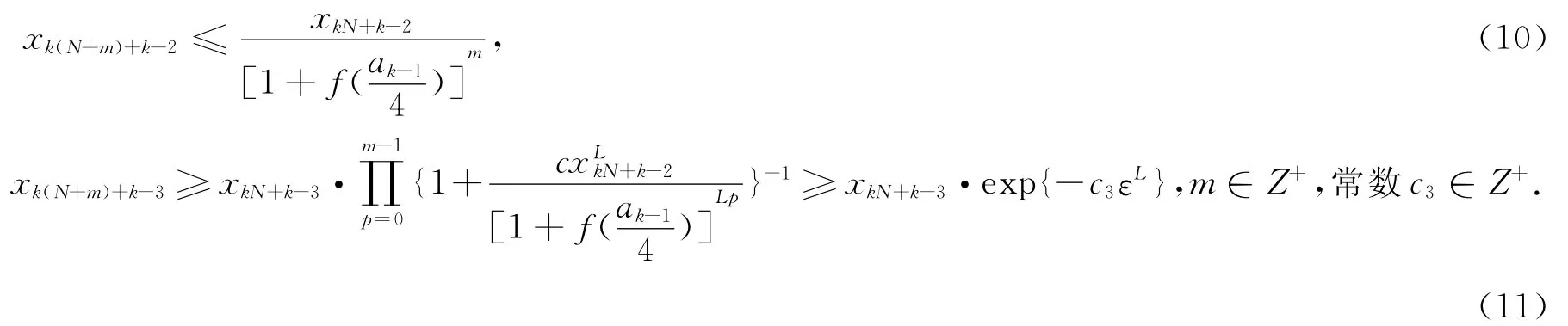
当ε充分小时，必有因此若对所有的N∈Z＋，有xkN＋k－3＞0，则

n是差分方程（2）若存在N∈Z＋，使xkN＋k－3＝0，则选定y｛｝的1个解，使得yk－3＞0，则ykN＋k－3＞0.由前面讨论知，若则对充分小的ε有，所以对任意的n＞N有ykn＋k－3＜ykN＋k－3＜ε＋xkN＋k－3＜2ε，即类似 于 （10）和 （11）式 的 证 明 得即产 生 矛 盾 ，因 此成立.综上所述，当k为偶数时方程（3）的解是稳定的.

情况2k为奇数.假设xnk＋i→ai（n→ ∞），其中ai≥0，i＝0，1，…，k－1.当ak－1≠0时，类似于情况1有：ak－2＝0，ak－3≠0，ak－4＝0，…，a2≠0，a1＝0，a0≠0.然而由有产生矛盾 当a＝0，a≠0时，用情况 中的证明方法得到a≠0，产生矛盾因此有a0＝a1＝a2＝…＝ak－1＝0.此情况类似于情况1中的iii），易证结论成立，因此当k为奇数时方程（3）的解也是稳定的.

由定理1可知方程（2）的所有解是收敛的，它们或者收敛到某点（a0，0，…，ak－2，0），或者收敛到某点（0，a1，…，0，ak－1）.讨论收敛域.当k为奇数时有xnk＋i→0，其中i＝0，1，…，k－1，所以方程（2）的源于Rk＋的解的收敛域也是Rk＋，因此我们只需考虑k为偶数时的情形.

定理2 考虑方程（1），其中k为偶数，f和g是［0，＋∞）上连续函数，g＞0，fg在［0，＋∞）上递增，f非负且对任意a≥0满足条件

则有：①对于使方程（1）收敛于（a0，0，…，ak－2，0）的解的初始点的集合是形如｛（y0，y1，…，且对每个yj（j＝1，3，…，k－1）存在唯一连续增函数使其中aj－1≥0｝的集合.② 对于使方程（1）收敛于（0，a1，…，0，ak－1）的解的初始点的集合是形如｛（y0，y1，…，且对每个yj（j＝1，3，…，k－1）存在唯一连续增函数hj∶［aj，＋∞）→ ［0，＋∞），使hj（yj）＝yj－1，其中aj－1≥0｝的集合.为证明定理2，我们先建立一些引理.

引理1［1］若f是［0，＋∞）上非负连续递增函数，且对于a＝0满足（13）式，则对任意ζ＞0，存在ξ＞0，使得对任意x∈ ［0，ξ］，存在常数c＞0有cxL2（0）＋ζ≤f（x）≤cxL2（0）－ζ.

引理2 设序列｛xn｝满足定理2的条件.记且j＝1，3，…，k－1），则

引理3 设f满足定理2的条件，y＝x＞0且y＝rx＞0（r＞1，j＝1，3，…，k－1）.

引理4 设f满足定理2的条件，yj＝rjxj＞0且0＜yj－1＜xj－1（rj＞1，j＝1，3，…，k－1）.

证明 引理1—4的证明与文献［2］中相应引理的证明类似，故证明省略.

定理2的证明 当方程（1）的解是平凡解时，定理显然成立.现讨论方程（1）的解是非平凡的情况.由引理1及f是连续的，且g＞0，知fg满足定理1中f的条件.由于证明定理1的开始有：

或者

因此设（h（x），x，h（x），x，…，h（x），x）为收敛到（0，a，…，0，a）的解的初始值的集合，设是收敛到（a0，0，…，ak－2，0）的解的初始值的集合.分4步来讨论：

i）首先证明存在性.先考虑解收敛到（a0，0，…，ak－2，0）（ai≥0，i＝0，2，…，k－2）的情况，即对每个xj＞0（j＝1，3，…，k－1），存在xi≥ai（i＝0，2，…，k－2）使得（xkn，xkn＋1，…，xkn＋k－2，xkn＋k－1）→（a0，0，…，ak－2，0）成立.显然（0，xkn＋1，0，xkn＋3，…，0，xkn＋k－1）→ （0，x1，0，x3，…，0，xk－1）.由此断言对任意δ＞0，能选出足够大的x（δ）i（i＝0，2，…，k－2），使得以（x（δ）0，x1，x（δ）2，x3，…，x（δ）k－2，xk－1）为初始条件经N步递推得到x（δ）kN＋i＞2ai（i＝0，2，…，k－2）和xkN＋j＜δ（j＝1，3，…，k－1）.事实上，x（δ）kN＋i＝2，…，k－2），取x（δ）i≥max｛2ai，1｝［1＋f（xi＋1）g（xi＋1）］N（i＝0，2，…，k－2），使x（δ）kN＋i＞max｛2ai，1｝（i＝0，2，…，k－2）.选取足够大的N，使

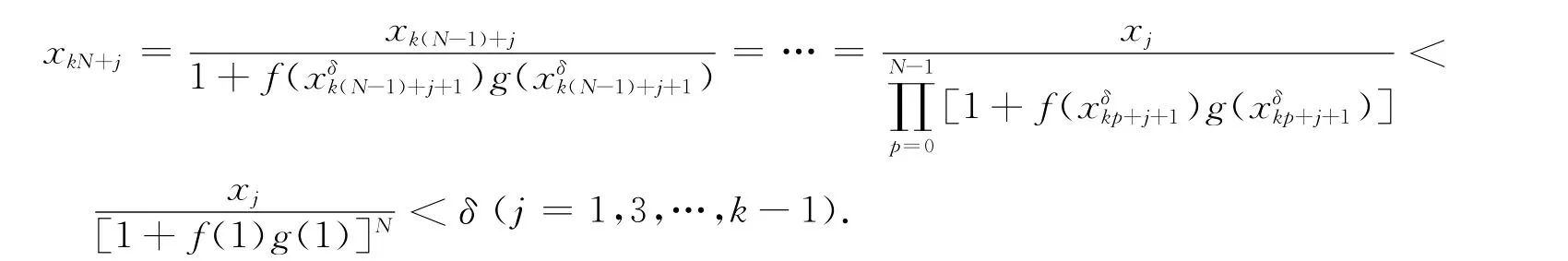
为了简便，称初始值为（x0，x1，…，xk－1）的序列（xkn，xkn＋1，…，xkn＋k－1）的收敛性为初始值（x0，x1，…，xk－1）的收敛性.我们先考虑初始值（x（δ）kN，xkN＋1，x（δ）kN＋2，xkN＋3，…，x（δ）kN＋k－2，xkN＋k－1）和（x（δ）kN，0，x（δ）kN＋2，0，…，x（δ）kN＋k－2，0）的收敛性.显然（x（δ）0，x1，x（δ）2，x3，…，x（δ）k－2，xk－1）和（x（δ）kN，xkN＋1，x（δ）kN＋2，xkN＋3，…，x（δ）kN＋k－2，xkN＋k－1）收敛到同1个点.由于（x（δ）kN，0，x（δ）kN＋2，0，…，x（δ）kN＋k－2，0）是Rk＋上的1个固定点，且x（δ）kN＋i＞2ai（i＝0，2，…，k－2），则由定理1，选取充分小的δ＞0，有，x1，x（δ）2，x3，…，x（δ）k－2，xk－1）和（x（δ）kN，xkN＋1，必收敛到1个点，记为（b0，0，b2，0，…，bk－2，0），且bi＞ai，（i＝0，2，…，k－2）.固定xj≥0（j＝1，3，…，k－1），设x′i＝inf｛xi≥0∶（x0，x1，…，xk－2，xk－1）→ （c0，0，…，ck－2，0）且cj≥aj（j＝0，2，…，k－2）｝（i＝0，2，…，k－2）.由于（x（δ）0，x1，…，x（δ）k－2，xk－1）→（b0，0，…，bk－2，0），且bi＞ai，（i＝0，2，…，k－2），所以x′i（i＝0，2，…，k－2）必存在.分两种情况讨论：

① 假设（x′0，x1，x′2，x3，…，x′k－2，xk－1）→ （b′0，0，b′2，…，b′k－2，0），且b′i≥ai（i＝0，2，…，k－2）.若b′i＝ai（i＝0，2，…，k－2），则存在性成立；若 ∃i0∈ ｛0，2，…，k－2｝使b′i0＞ai0，不失一般性，假设i0＝0，则由定理1，可选取充分小的δ＞0，使（x′0－δ，x1，x′2，x3，…x′k－2，xk－1）→ （b″0，0，b″2，0，…，b″k－2，0）且b″0＞a0，b″i≥ai（i＝2，…，k－2），那么由上可知inf｛x0≥0∶（x0，x1，…，xk－2，xk－1）→ （c0，0，…，ck－2，0）且cj≥aj（j＝0，2，…，k－2）｝≤x′0－δ，产生矛盾，所以b′0＝a0.

② 假设（x′0，x1，x′2，x3，…，x′k－2，xk－1）→ （b′0，0，b′2，0，…，b′k－2，0），且 ∃i0∈ ｛0，2，…，k－2｝使b′i0＜ai0，b′j≥aj（j∈ ｛0，2，…，k－2｝，j≠i0）.不妨设i0＝0，或者（x′0，x1，x′2，x3，…，x′k－2，xk－1）→ （0，b′1，0，b′3，…，0，b′k－1），且b′j≥0（j＝1，3，…，k－1）.则由定理1，可选取充分小的δ＞0，使得或者（x′＋δ0，x1，x′2，x3，…，x′k－2，xk－1）→ （b″0，0，b″2，0，…，b″k－2，0），且b″0＜a0；或者（x′0＋δ，x1，x′2＋δ，x3，…，x′k－2＋δ，xk－1）→ （0，b″1，0，b″3，…，0，b″k－1），且b″j＞0（j＝1，3，…，k－1）.这意味着inf｛x0≥0∶（x0，x1，…，xk－2，xk－1）→ （c0，0，…，ck－2，0）且cj≥aj（j＝0，2，…，k－2）｝≥x′0＋δ，所以产生矛盾.综上存在性成立.对于以（0，a1，…，0，ak－1）（aj≥0，j＝1，3，…，k－1）为收敛点的情况，证明类似.

ii）¯hj（yj）＝yj－1，hj（yj）＝yj－1（j＝1，3，…，k－1）均为函数.先考虑解收敛到（a0，0，…，ak－2，0）（ai≥0，i＝0，2，…，k－2）的情况.若xj＝0（j＝1，3，…，k－1），为了使（x0，x1，…，xk－2，xk－1）→（a0，0，…，ak－2，0），必有xi＝ai（i＝0，2，…，k－2）.因此假设xj＞0（j＝1，3，…，k－1），xi＞0（i＝0，2，…，k－2），显然为使（x0，x1，…，xk－2，xk－1）→ （a0，0，…，ak－2，0）必有xi＞ai（i＝0，2，…，k－2）.所以只需证明：对于给定的2个初始条件（x0，x1，…，xk－2，xk－1）和（y0，y1，…，yk－2，yk－1），若yj＝xj，yj－1≥xj－1，且和则yj－1＝xj－1（j＝1，3，…，k－1）.设yj－1≥rj－1xj－1（rj－1＞1，j＝1，3，…，k－1）.由引理2有但由引理3知，当N充分大，n≥N时，又有，产生矛盾，因此yj－1＝xj－1（j＝1，3，…，k－1），并说明为1个函数.

对于以（0，a1，…，0，ak－1）（aj≥0，j＝1，3，…，k－1）为收敛点的情况，可类似地证明hj（yj）＝yj－1（j＝1，3，…，k－1）为1个函数，但此时需对引理2做些改动：记a－1＝ak－1.若且则

iii）（yj）＝yj－1，hj（yj）＝yj－1（j＝1，3，…，k－1）均为单调递增函数.先考虑解收敛到（a0，0，…，ak－2，0）（aj－1＞0，j＝1，3，…，k－1）的情况.由方程（1）显然有（0）＝aj－1，且对于每个xj＞0有¯hj（xj）＞aj－1（j＝1，3，…，k－1），因此只需考虑初始点（x0，x1，…，xk－2，xk－1）当xi＞0（i＝0，1，2，…，k－1）的情况.先假设（xj－1，xj）和（yj－1，yj）是曲线¯hj上的点，且0＜xj＜yj和0＜yj－1＜xj－1（j＝1，3，…，k－1），所以 ∃rj＞1，使yj≥rjxj（j＝1，3，…，k－1）.由引理2知，对于充分大的N，当n≥N时，有又 由 引 理 4 有，产生矛盾，因此3，…，k－1）为单调递增函数.对于以（0，a1，…，0，ak－1）（aj≥0，j＝1，3，…，k－1）为收敛点时，同理可证明hj（yj）＝yj－1（j＝1，3，…，k－1）为单调递增函数.

推论1 考虑方程（2），其中k为偶数，f是［0，＋∞）上非负连续递增函数，若对任意a≥0，f满足条件

则有：①对于使方程（2）收敛于（a0，0，…，ak－2，0）的解的初始点的集合是形如｛（y0，y1，…，且对每个yj（j＝1，3，…，k－1）存在唯一连续增函数使其中aj－1≥0｝的集合.② 对于使方程（2）收敛于（0，a1，…，0，ak－1）的解的初始点的集合是形如｛（y0，y1，…，且对每个yj（j＝1，3，…，k－1）存在唯一连续增函数hj∶［aj，＋∞）→ ［0，＋∞），使hj（yj）＝yj－1，其中aj－1≥0｝的集合.

注［1］：如果f∈C1（［0，＋∞）），且满足f在［0，＋∞）递增则对所有a≥0，（14）和（15）式成立.

文献［2］中列举的适合定理条件的f和g的形式同样适合本文定理2和推论1.此外，当α＞0，β＞0时，形如f（x）＝αxβ，g（x）＝c＋ax（a＞1，－1＜c＜＋∞）或g（x）＝c＋arctanx（0＜c＜＋∞）的函数适合定理2中f和g的条件，进而f和g的乘积也适合推论1中f的条件.

注［2］：当k＝2时，方程（2）为文献［1］中的方程，因此本文的结果包含了文献［1］中的结果.

［1］Steven Kalikow，Peter MKnopf，Ying Sue Huang，Gabor Nyerges.Convergence Properties in the Nonhyperbolic Casexn＋1＝xn－1／［1＋f（xn）］［J］.J Math Anal Appl，2007，326：456－467.

［2］Hou Cheng－min.Convergent Properties of Solutions of Higher Order Difference Equationsxn＋1＝xn－k1＋f（xn）g（xn）［J］.延边大学学报：自然科学版，2011，37（1）：30－38.

［3］Kent C M.Convergence of Solutions in a Nonhyperbolic Case［J］.Nonlinear Anal，2001，47：4651－4665.

［4］Kulenovi′c MR S，Ladas G.Dynamics of Second Order Rational Difference Equations［M］.Boca Raton：Chapman＆ Hall／CRC，2002.

Stability Properties of a Class of Higher Order Difference Equations

GE Qi，HOU Cheng－min
（DepartmentofMathematics，Collegeofscience，YanbianUniversity，Yanji133002，China）

We studied the stability of the solution of the nonlinear difference equationsxn＝wherek∈ ｛2，3，…｝，fgis a continuous nonnegative increasing functions on［0，＋ ∞）.Whenkis even，we sho wthat the set of initial values such that corresponding solutions of converge to（a0，a1，…，ak－1）is the set of points of the form （y0，y1，…，yk－1）∈ ［a0，＋∞）×［a1，＋ ∞）× … × ［ak－1，＋ ∞）（ai≥0，i＝0，1，…，k－1），moreover exist some unique continuous increasing functionshi∶［ai，＋ ∞）→ ［ai－1，＋ ∞）such thathi（yi）＝yi－1（i＝1，3，…，k－1）.

difference equations；nonlinear；stability

O175.8

A

1004－4353（2011）03－0201－07

2011 -04 -13

葛琦（1973—），女，副教授，研究方向为泛函分析.

国家自然科学基金资助项目（11161049）；延边大学科研项目（延大科合字［2010］第004号）