利用腔QED技术实现特殊三粒子W态的隐形传送
2011-01-23计新
计 新
(延边大学理学院 物理系,吉林 延吉133002)
利用腔QED技术实现特殊三粒子W态的隐形传送
计 新
(延边大学理学院 物理系,吉林 延吉133002)
提出一个在腔QED中实现特殊三粒子W态的隐形传送方案.在方案中用3个二粒子纠缠态作为量子通道,通过原子与腔及经典场之间的相互作用以及适当的幺正变换,以成功几率1实现了特殊三粒子W态的传送.此外,本方案不需要联合贝尔测量,对腔衰减和热场也不敏感.
量子隐形传送;三原子纠缠W态;腔QED
0 引言
由于近些年量子力学的迅猛发展,量子纠缠在量子计算、量子信息处理、量子密集编码、量子密钥分配和量子隐形传送等方面起了很重要的作用[1-5].自1993年Bennett等人[3]提出未知单粒子量子态的隐形传送方案以来,隐形传态已成为量子信息领域倍受关注的焦点,并且在量子信息领域发挥着越来越重要的作用,因此,如何成功地传送1个纠缠态是非常关键的.近年来,人们提出许多可行的二粒子纠缠态的量子隐形传送方案[6-9].Lu和 Guo[6]通过用2个 Einstein-Podolsky-Rosen(EPR)粒子对作为量子通道传送1个二粒子纠缠态;Shi[7]和 Ye[8]等分别用非最大纠缠和最大纠缠 Greeberger-Horne-Zeilinger(GHZ)态作为量子通道实现了二粒子态的传输;Cao和Song[9]利用 W态作为量子通道实现了二粒子态的传输;Cola和Paris[10]以单个EPR粒子对作为量子通道,在外加粒子的辅助下来传送1个未知的二粒子纠缠态;Cao和Li[11]用团簇态作为量子通道传送1个未知的原子态,在其方案中单粒子测量取代了贝尔测量.与二粒子纠缠态相比,多粒子纠缠态有着更多的优点和更加广泛的应用性,因此一些传送多粒子态的方案相继被提出.Dai等人[12]用三粒子纠缠态和三粒子W态作为通道概率性地传送了1个三粒子纠缠态;查新未等[13]提出用三粒子 W态作为量子通道传送N粒子GHZ态的方案;Zhan等人[14]提出利用2个非最大四粒子纠缠态或4个二粒子部分纠缠态来传输四粒子纠缠W态的方案;郑亦庄等[15]提出利用3个二粒子最大纠缠态作为量子通道,并外加1个辅助粒子来传送三粒子纠缠W态.在文献[6-10]的方案中,需要对粒子进行联合贝尔测量,而且以上诸多方案中,用多粒子态作为量子通道或在外加辅助粒子的情况下完成传输任务,这无疑提高了对通道的要求.考虑到制备二粒子态相对比较容易,本文利用腔QED技术,以3个二粒子最大纠缠态作为量子通道,在不需要外加辅助粒子的情况下实现了特殊三粒子W态的传送.本方案不受腔衰减的影响,并且不需要联合贝尔测量,因此,基于目前的腔QED技术本方案是可行的.
假设要传送的三粒子纠缠W态为

其中a,b,c,d都是实数,并且满足归一化关系.构成量子通道的3个最大纠缠二粒子态分别为:

其中原子4、5、6为Alice所拥有,原子7、8、9为Bob所拥有.整个系统初始时刻的状态为
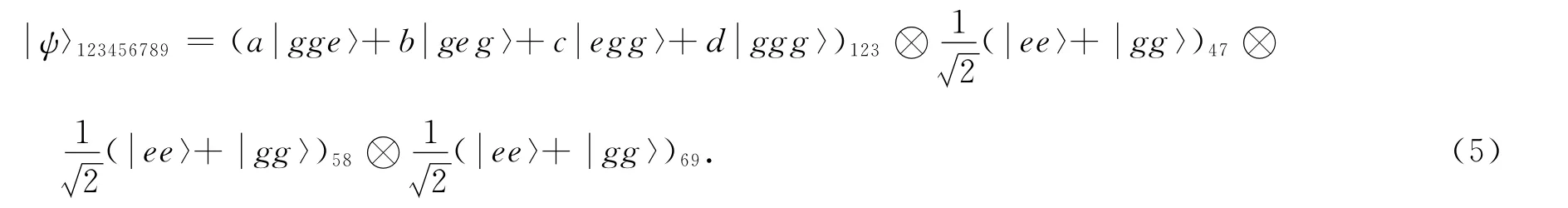
为了实现量子隐形传送,Alice分别把3对原子(1,4)、(2,5)和(3,6)依次通入腔中,同时用经典场驱动这3对原子.在旋波近似条件下,原子和腔场的相互作用哈密顿为[16]
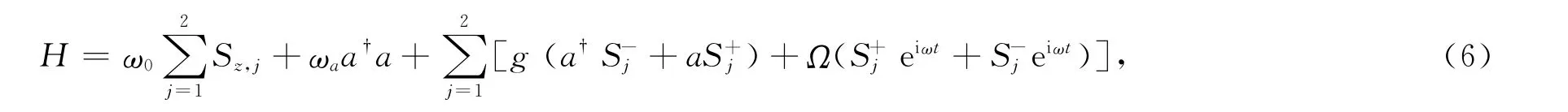
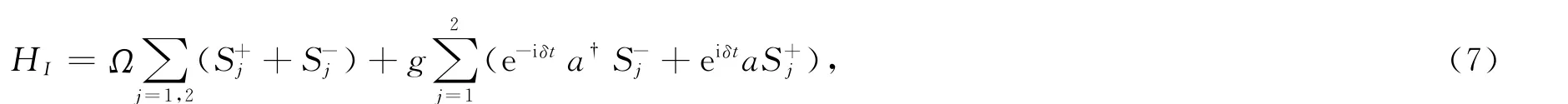
其中δ是原子跃迁频率ω0和腔场频率ωa的失谐量.如果Ω≫g,δ≫g,在原子系统和腔之间没有能量交换,所以腔衰减的影响被有效地消除.在相互作用绘景下,有效相互作用哈密顿为[16]

其中λ=g2/2δ.由此可以看出有效相互作用哈密顿不依赖腔场的态,因此,热场的影响可以消除.系统的演化算符为

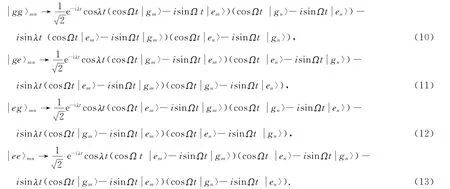
这里mn表示原子对(1,4)、(2,5)和(3,6).如果我们适当地选择相互作用时间t和拉比频率Ω,使λt=π/4,Ωt=π,则整个系统的态将演化为
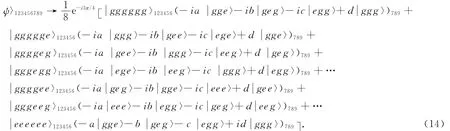
现在Alice对原子1、2、3、4、5、6进行单粒子探测,并通过经典通信把测量结果告诉Bob,Bob根据他接收到的测量结果,通过对7、8、9粒子做相应的幺正变换,就可以重新构建Alice所要传送的态.不失一般性,我们假设测量结果是则原子7、8、9所处的态将会塌缩到
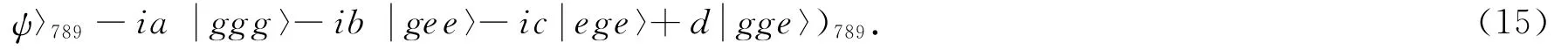
本文提出的方案优点有:①用二粒子纠缠态作为量子通道,并且不需要外加辅助粒子,既简化了对通道的要求,又节省了纠缠资源;②只需对原子进行单粒子测量而不是联合贝尔测量,简化了实验上的复杂度;③此方案不受腔衰减和热场的影响,并且成功几率是1.因此,基于目前的科学技术水平,本方案是可行的.
[1] Einstein A,Podolsky B,Rosen.Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?[J].Phys Rev A,1935,47(10):777.
[2] Schr¨odinger E.Die Gegen Wartige Situation in Quantenmechanik[J].Naturwissenschaften,1935,23:844.
[3] Bennett C H,Brassard G,Crepeau C.Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels[J].Phys Rev Lett,1993,70(13):1895.
[4]Bennett C H,Wiesner S J.Communication via One and Two-particle on Einstein-Podolsky-Rosen States[J].Phys Rev Lett,1992,69(20):2881.
[5]Akert A K.Quantum Cryptography Bases on Bell’s Theorem [J].Phys Rev Lett,1991,67(6):661.
[6]Lu H,Guo G C.Teleportation of a Two-particle Entangled State via Entanglement Swapping[J].Phys Lett A,2000,276(5-6):209.
[7]Shi B S,Jiang Y K,Guo G C.Probabilistic Teleportation of Two-particle Entangled State[J].Phys Lett A,2000,268(3):161.
[8]Ye L,Yao C M,Guo G C.Teleportation of a Two-particle Entangled State[J].Chin Phys,2001,10(11):1001.
[9]Cao Z L,Song W.Teleportation of a Two-particle Entangled State via W Class State[J].Phys A,2005,347:177.
[10]Cola MM,Paris MG A.Teleportation of Bipartite States Using a Single Entangled Pair[J].Phys Lett A,2005,337(1/2):10.
[11]Cao Z L,Li D C.Scheme for Teleportation of an Unknown Atomic State via a Cluster State in Cavity QED[J].Chin Phys B,2008,17(1):55.
[12]Dai H Y,Li C Z,Chen P X.Probabilistic Teleportation of the Three-particle Entangled State by the Partial Three-particle Entangled State and Three-particle Entangled W State[J].Chin Phys Lett,2003,20(8):1196.
[13]查新未,张淳民.利用一个三粒子 W态隐形传送N粒子GHZ态[J].物理学报,2008,57(3):1339.
[14]Zhan Y B,Fu H.Probabilistic Teleportation of a Four-particle Entangled State[J].Commu Theor Phys,2005,43(1):440.
[15]郑亦庄,戴玲玉,郭光灿.三粒子纠缠 W 态的隐形传态[J].物理学报,2003,52(11):2678.
[16]Zheng S B.Generation of Entangled States for Many Multilevel Atoms in a Thermal Cavity and Ions in Thermal Motion[J].Phys Rev A,2003,68:035801.
Teleportation of a Three-atom Entangled W State Using Three EPR Pairs in Cavity QED
JI Xin
(DepartmentofPhysics,CollegeofScience,YanbianUniversity,Yanji133002,China)
We proposed a scheme for teleporting a three-atom entangled W state in cavity QED.In the scheme,three EPR pairs are chosen as quantum channel shared by the sender and the receiver.By using atom-cavityfield interaction and appropriate unitary transformations,the three-atom entangled W state can be teleported successfully with probability 1.0.Moreover,the scheme does not need joint Bell measurement and is insensitive to the cavity decay and thermal field.
quantum teleportation;three-atom entangled W state;cavity QED
O431
A
1004-4353(2011)03-0234-04
2011 -06 -24
国家自然科学基金资助项目(11064016;61068001)
计新(1965—),女,副教授,研究方向为量子光学与量子信息学.
