非对称Dyck路的三个计数结果

,

(徐州师范大学 数学科学学院,江苏 徐州 221116)

0 引言

格路计数问题是组合数学主要研究问题之一,多年来备受国内外学者的关注.最近,Deutsch等人[1-2]定义了一种新的格路(非对称Dyck路),讨论了其性质,并给出了计数公式.本文主要考虑非对称Dyck路在固定半长和左步时,带有峰、谷、双升等参数的计数问题.

1 预备知识

定义1[1]平面上起点和终点都在x轴,且不向下越过x轴,由上升步U(1,1),下降步D(1,-1),左步L(-1,-1)构成步集,且上升步和左步不重叠的路,我们称之为非对称Dyck路.我们用M表示所有的非对称Dyck路集,则M中任一非空路都可以被唯一的表示为Uα1Dα2或Uα3L的形式,其中α1,α2,α3∈M且α3≠ε(ε表示空路).

Lagrange反演定理[3]设A(z)满足等式A(z)=1+zH(A(z)),此处H(λ)是关于λ的多项式,且上式有唯一解A(z),设G(λ)是关于λ的多项式,则有

引理1[4]峰的个数为l,半长为n的Dyck路的条数为

引理2[4]谷的个数为t,半长为n的Dyck路的条数为

引理3[4]双升的个数为m,半长为n的Dyck路的条数为

引理4[2]左步数s,半长为n的非对称Dyck路的条数为

2 主要结果

1)F(x,y,z)=1+z[F(x,y,z)(F(x,y,z)-1)+yF(x,y,z)+x(F(x,y,z)-1)].

证明1)由于任一非空的非对称Dyck路γ都可以唯一地分解为如下三种形式之一

Uα1Dα2;UDα3;Uα4L;(α1,α4≠ε),

从而我们得到

F(x,y,z)=1+zF(x,y,z)(F(x,y,z)-1)+zyF(x,y,z)+zx(F(x,y,z)-1),

即

F(x,y,z)=1+z[F(x,y,z)(F(x,y,z)-1)+yF(x,y,z)+x(F(x,y,z)-1)].

2)令A(z)=1+zH(A(z)),H(λ)=λ(λ-1)+yλ+x(λ-1),其中A(z)=F(x,y,z),则由Lagrange反演定理得

令σ-t+k=σ-1,则

所以

即

左步数为s,峰的个数为t,半长为n的非对称Dyck路的条数为

注1 当s=0时,则非对称Dyck路变成普通的Dyck路,由此可知:含有t个峰,半长为n的Dyck路的条数at,n为

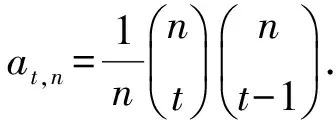
注2 对t=1,2,…,n求和,可知左步数为s半长为n的非对称Dyck路的条数为

此结果与引理4结论一致.

1)F(x,y,z)=1+z[yF(x,y,z)(F(x,y,z)-1)+F(x,y,z)+x(F(x,y,z)-1)];

证明由于任一非空的非对称Dyck路γ都可以唯一的分解为如下三种形式之一

Uα1Dα2；Uα3D；Uα4L;(α2,α4≠ε),

则有

F(x,y,z)=1+zyF(x,y,z)(F(x,y,z)-1)+zF(x,y,z)+zx(F(x,y,z)-1).

即

F(x,y,z)=1+z[yF(x,y,z)(F(x,y,z)-1)+F(x,y,z)+x(F(x,y,z)-1)].

令A(z)=1+zH(A(z)),H(λ)=yλ(λ-1)+λ+x(λ-1),其中A(z)=F(x,y,z),则由Lagrange反演定理得

所以

令s+t+m=σ-1,则

所以

即

故左步数为s,谷的个数为t,半长为n的非对称Dyck路的条数为

注3 当s=0时,则非对称Dyck路变成普通的Dyck路,含有t个谷,半长为n的Dyck路数为

此结果与引理2的结果一致.

1)F(x,y,z)=1+z[yF(x,y,z)(F(x,y,z)-1)+F(x,y,z)+xy(F(x,y,z)-1)].

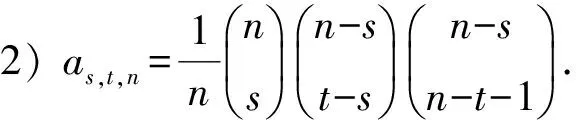
证明由于任一非空的非对称Dyck路γ都可以唯一的分解为如下三种形式之一

Uα1Dα2；UDα3；Uα4L;(α1,α4≠ε),

故有

F(x,y,z)=1+zyF(x,y,z)(F(x,y,z)-1)+zF(x,y,z)+zxy(F(x,y,z)-1).

令A(z)=1+zH(A(z)),H(λ)=yλ(λ-1)+λ+xy(λ-1),其中A(z)=F(x,y,z),则由Lagrange反演定理得

所以

令s+l=t,l+s+m=σ-1,则

所以

即

故左步数为s,双升的个数为t,半长为n的非对称Dyck路的条数为

注4 当s=0时,则非对称Dyck路变成普通的Dyck路,故含有t个双升,半长为n的Dyck路数为

此结果与引理3的结果一致.

[1]Deutsch E,Munarini E,Rinaldi S.Skew Dyck paths area and superdiagonal bargraphs[J].Journal of Statistical Planning and Inference,2010,140:1550-1562.

[2]Deutsch E,Munarini E,Rinaldi S.Skew Dyck paths[J].Journal of Statistical Planning and Inference,2010,140:2191-2203.

[3]Rogers D,Shapiro G,Deques L W.Trees and lattice paths[M].Lecture Notes in Mathematics,1981,884:293-303.

[4]Deutsch E.Dyck path enumeration[J].Discrete Mathematics,1999,204:167-202.