一类分数阶多点边值共振问题解的存在性

,

(中国矿业大学 理学院,江苏 徐州 221008)

0 引言

分数阶导数是整数阶导数的推广.近些年来,分数阶导数及分数阶微分方程在科学、工程和数学等领域得到了重要应用,例如已成功应用于粘弹性材料、信号处理、控制、生物等领域[1].值得注意的是,分数阶微分方程的理论研究刚起步,分数阶微分方程边值问题作为分数阶微分方程理论研究的重要分支之一,近年来得到研究者们的重视,也获得了不少研究成果,如文献[2-15].在文[5]中,作者研究了如下边值问题

其中n>2,n-1<α≤n,其核是一维的,运用Mawhin连续性定理得出解的存在性,本文受此启发研究分数阶多点边值问题(其核是二维的)

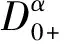
(1)

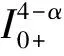
(2)

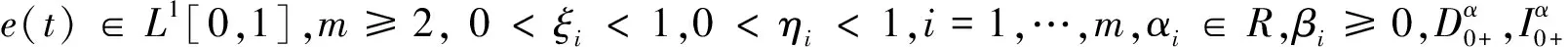
其中Γ(·)是Gamma函数,为了证明BVP(1)(2)有解及计算的方便,使用下面的假设:

(C2): Λ=Λ1Λ4-Λ2Λ3≠0.

1 预备知识

首先介绍一些关于迭合度的基本理论:

设Y,Z是实Banach空间,L:domL⊂Y→Z是一个指标为零的Fredholm算子,P:Y→Y,Q:Z→Z是连续投影算子且满足

ImP=KerL,KerQ=ImL,Y=KerL⨁KerP,Z=ImL⨁ImQ.

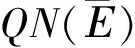
定义1[2]函数y:(0,+∞)→R的α阶Riemann-Liouville分数阶积分为

其中α>0,Γ(·)为Gamma函数.

定义2[2]连续函数y:(0,+∞)→R的α阶Riemann-Liouville分数阶导数为

其中α>0,Γ(·)为Gamma函数,n=[α]+1.

其中N为大于或等于α的最小整数.

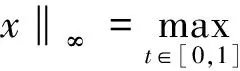
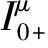
(3)

其中x∈[0,1],ci∈R,I=1,2,…,N-1,其范数为

易证得Cμ[0,1]是Banach空间.

引理2[5]f⊂Cμ[0,1]是连续紧当且仅当f是一致有界且等度连续.

这里一致有界是存在M>0,使得对任意u∈f有

等度连续是只对∀ε>0,∃δ>0使得

|u(t1)-u(t2)|<ε,(∀t1,t2∈[0,1],|t1-t2|<δ,∀u∈f)，

且

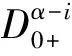
定理1[6](Mawhin连续性定理) 设Ω⊂Y是一个有界开集,L是一个指标为零的Fredholm算子,N是L-紧的,如果下面条件成立:

(i)Lx≠λNx.∀(x,λ)∈[domLKerL∩∂Ω]×[0,1];

(ii)Nx∉ImL,∀x∈KerL∩∂Ω;

(iii)deg(JQN|KerL,KerL∩Ω,0(≠0,

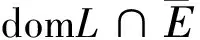
2 主要结果

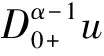
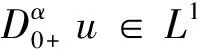
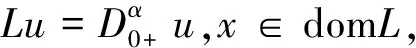
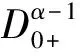
则边值问题(1)、(2)就转化为Lu=Nu.

引理3 假设(C1)(C2)成立,则L:domL⊂Y→Z是一个指标为零的Fredholm算子,投影算子Q:Z→Z定义为

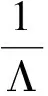
(4)

其中

线性算子Kp:ImL→domL∩KerP记为

证明显然有KerL={x∈domL:u=atα-1+btα-3.a,b∈R,t∈[0,1]}≅R2现在来证明

ImL={y∈Z:Q1y=Q2y=0}

(5)

方程

(6)

有解x(t)满足(2)的充要条件是

Q1y=Q2y=0

(7)

事实上,若解x(t)满足(2),则从(6)式有

根据条件(C1),得到

Q1y=Q2y=0.

另一方面,如果(7)式成立,由(2)知,

其中a,b是任意常数,则易知u(t)是方程(6)且满足(2)式的解,从而(5)式成立.

令

因此

Qy(t)=(T1y(t))tα-1+(T2y(t))tα-3,

易知dimImQ=2

又有

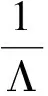
依次可求得

T1(T2ytα-3)=0,T2(T1ytα-1)=0,T2((T2y)tα-3)=T2y,

因此

Q2y=Q((T1y)tα-1+(T2y)tα-3)=Qy,

所以Q是投影算子.

下证KerQ=ImL,如果y∈KerQ,由Qy=0有

而又(C2)成立,故Q1y=Q2y=0,所以y∈ImL.若y∈ImL,由Q1y=Q2y=0,易知Qy=0,所以y∈KerQ,故KerQ=ImL.

对∀y∈Z,有y=(y-Qy)+Qy,则有y-Qy∈KerQ=ImL,Qy∈ImQ,所以Z=ImL+ImQ,下证ImL∩ImQ={0},

令y=atα-1+btα-3,且y∈ImL∩ImQ知,y∈ImL,故有Q1y=Q2y=0

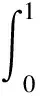
易求得

又(C2)成立,所以a=b=0,即ImL∩ImQ={0},故Z=ImL⨁ImQ且dimKerL=dimImQ=co dimImL=2

故L是指标为零的Fredholm算子.

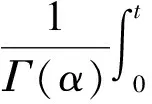
(8)

事实上,∀y∈ImL有

而当u∈domL∩KerP,我们有

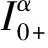
由于u∈domL∩KerP,由(2)及Pu=0,因此得到

(KPL)u(t)=u(t),

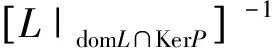
因此,由(8)我们有

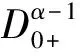
所以

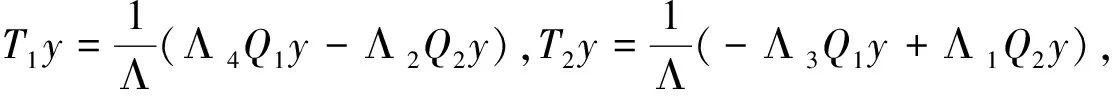
QNx(t)=(T1Nx)tα-1+(T2Nx)tα-3,

且

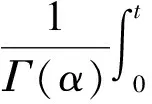
由引理2 类似的证明方法,我们得到如下引理.

引理4 对任意e∈L1[0,1],Kp(I-Q):Y→Y是全连续的.

定理2 如果条件(C1)(C2)成立,假设满足下面条件:

1)存在函数a(t),b(t),c(t),d(t),f(t),r(t)∈L1[0,1]及常数θ∈[0,1)对∀(x,y,z,w)∈R4,t∈[0,1]有

|f(t,x,y,z,w)|≤a(t)|x|+b(t)|y|+c(t)|z|+d(t)|w|+f(t)|x|θ+r(t)

(9)

Q1Nx(t)≠0或Q2Nx(t)≠0.

3)存在实数B>0,a,b∈R,使得a2+b2>B,下面条件至少有一个成立

aT1N(atα-1+btα-3)+bT2N(atα-1+btα-3)>0

(10)

aT1N(atα-1+btα-3)+bT2N(atα-1+btα-3)<0

(11)

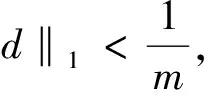
证明取Ω1={x∈domLKerL:Lx=λNx,λ∈[0,1]},下证Ω1是有界的.

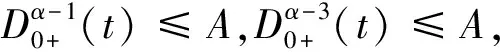
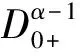
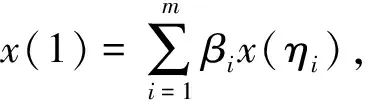
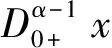
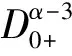
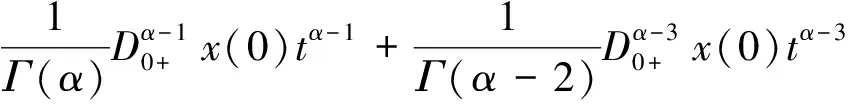
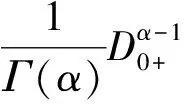
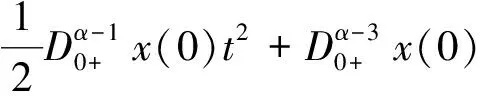
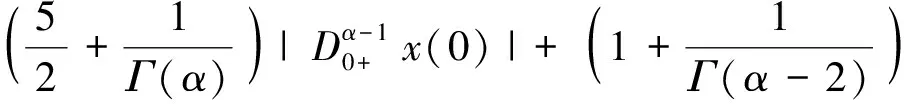
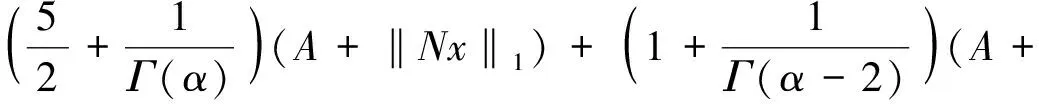
(12)

对∀x∈Ω1有(I-P)x∈domL∩KerP,LPx=0,根据引理3,我们有

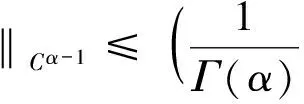
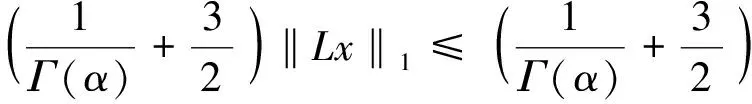
(13)

由(12)(13)知

‖x‖Cα-1≤‖(I-P)x‖Cα-1+‖Px‖Cα-1≤

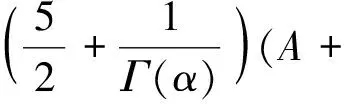
(14)

记

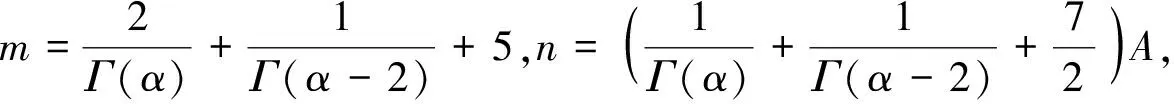
故

‖x‖Cα-1≤m‖Nx‖1+nA.

如果(9)式成立,根据(14)式我们有

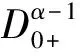
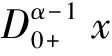
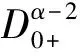
又因为

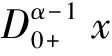
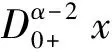
故

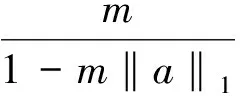
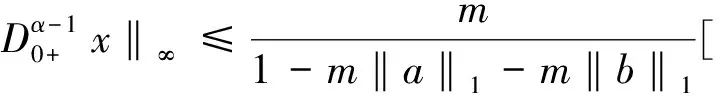
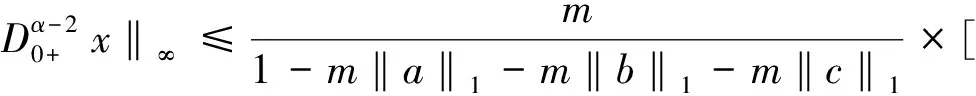
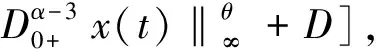
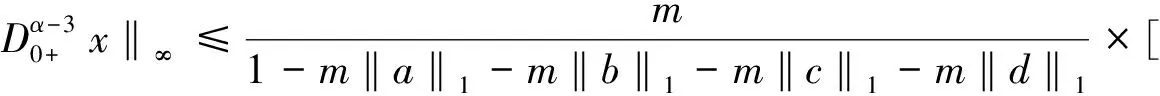
因为θ∈[0,1),由以上所得,故存在A1,A2,A3,A4>0,使得

因此

所以Ω1是有界的.取Ω2={x∈KerL:Nx∈ImL},下证Ω2是有界的.对任意的x∈Ω2,x∈KerL={x∈domL:x=atα-1+btα-3,a,b∈R,t∈[0,1]}以及QNx(t)=0,即

T1N(atα-1+btα-3)=T2N(atα-1+btα-3)=0,

由条件(3)得,a2+b2≤B,因此Ω2是有界的.

对于∀a,b∈R,t∈[0,1],定义线性同构J:KerL→ImQ为

J(atα-1+btα-3)=atα-1+btα-3,

若T1N(atα-1+btα-3)+T2N(atα-1+btα-3)>0成立.

取Ω3={x∈KerL:λJx+(1-λ)QNx=0,λ∈[0,1]}.

下证Ω3是有界的.

对任意x=atα-1+btα-3∈Ω3,因为λJx+(1-λ)QNx=0.

λ(atα-1+btα-3)=-(1-λ)[(T1N(atα-1+btα-3))tα-1+(T2N(atα-1+btα-3))tα-3]

如果λ=1,那么a=b=0,否则,如果a2+b2>B,由(10)知

λ(a2+b2)=-(1-λ)[aT1N(atα-1+btα-3)+bT2N(atα-1+btα-3)]<0,

故矛盾,由x∈Ω3,故

‖x‖Cα-1=‖atα-1+btα-3‖Cα-1=

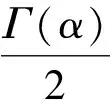
所以Ω3是有界的,同理可证

aT1N(atα-1+btα-3)+bT2N(atα-1+btα-3)<0,

成立

Ω3={x∈KerL:-λJx+(1-λ)QNx=0,λ∈[0,1]},

是有界的.

通过以上的讨论易知满足定理1的(i)(ii),下证定理1的(iii)也是满足的．

令H(x,λ)=±λJx+(1-λ)QNx,根据以上证明有H(x,λ)≠0,∀x∈∂Ω∩KerL因此,根据同伦不变性可得:

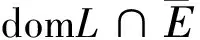
[1]Kilbas A,Srivastava A,Trujillo H M.J.Theory and Applications of Fractional Differential Equations[M].Elsevier,Amsterdam,2006.

[2]Bai Z,Lu H.Positive solutions for boundary value problem of nonlinear fractional differential equation[J].J Math Anal Appl,2005,311:495-505.

[3]Bai Z,Qiu T.Existence of positive solution for singular fractional differential equation[J].Appl Math Lett,2009,215:2761-2767.

[4]Su X.Boundary value problem for a coupled system of nonlinear fractional differential equations[J].Appl Math Lett,2009,22:64-69.

[5]Zhang Y,Bai Z.Existence of positive solutions for s nonlinear fractional three-point boundary value problen at resonance[J].Appl Math Comput,2010,19:411-418.

[6]葛渭高.非线性常微分方程边值问题[M].北京: 科学出版社,2007.

[7]Bai Z,Zhang Y.The existence of solutions for a factional multi-point boundary value problem [J].Appl Math Comput,2010,60:2364-2372.

[8]Agarwal R P,Lakshmikantham V,Nieto J J.On the concept of solution for fractional differential equations with uncertainty[J].Nonlinear Anal,2010,72: 2859-2862.

[9]Bai Z.On positive solutions of a nonlocal fractional boundary value problem[J].Nonlinear Anal,2010,72: 916-924.

[10]Ahmad B.Existence results for multi-point nonlinear boundary value problems of fractional differential equations[J].Mem Differ Equ Math Phys,2010,49:83-94.

[11]Kosmatov N.A multi-point boundary value problem with two critical conditions[J].Nonlinear Anal,2006,65: 622-633.

[12]Lakshmikantham V,Leela S.Nagumo-type uniqueness result for fractional differential equations[J].Nonlinear Anal,2009,71: 2886-2889.

[13]Lakshmikantham V,Leela S A.Krasnoselskii-Krein-type uniqueness result for fractional differential equations[J].Nonlinear Anal,2009,71: 3421-3424.

[14]Lakshmikantham V,Vatsala A S.Theory of fractional differential inequalities and applications[J].Commun Appl Anal,2007,11: 395-402.

[15]Lakshmikantham V,Vatsala A S.Basic theory of fractional differential equations[J].Nonlinear Anal,2008,69:2677-2682.