微积分学在经济分析中的应用
2011-01-18赖满瑢
赖 满 瑢
(厦门南洋职业学院,福建 厦门 361000)
在纷扰复杂瞬息万变的经济现象中揭示其背后深刻的经济原理离不开高等数学。而微积分是高等数学的核心,也是与经济学联系最紧密的纽带,是学好经济学的基础,在经济分析中具有重要的应用。
1 导数在经济分析中的应用
1.1 最优化分析
在工农业生产、科学技术研究、经营管理及实际生活中, 常常会碰到如何做才能使“产量最高”、“材料最省”、“耗时最少”、“效率最高”、“利润最大”、“成本最低”、“面积最大”等最优化问题,这些问题均为数学问题,即求函数的最大值和最小值问题。
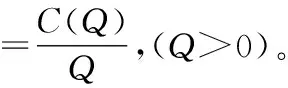
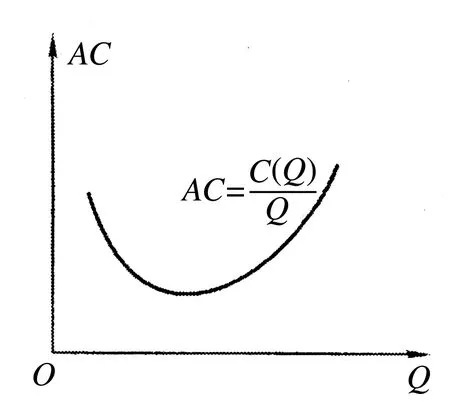
在经济学中,平均成本曲线一般如上图所示的形状,因此平均成本函数有最小值问题。
例:设某企业的总成本函数为C=C(Q)=0.3Q2+9Q+30,试求
(1)平均成本最低时的产出水平及最低平均成本;
(2)平均成本最低时的边际成本, 并与最低平均成本作比较。
(2)边际成本函数为:MC=0.6Q+9
平均成本最低时的产出水平Q=10,这时的边际成本为:MC|Q=10=0.6×10+9=15
综上可知,平均成本最低时的边际成本与最低平均成本相等,都为15.
上述结果不是偶然的,在产出水平Q能使平均成本最低时,必然有平均成本等于边际成本。
1.2 边际分析
对经济学中的函数而言, 因变量对自变量的导数称为“边际”。它表示自变量增量为1个单位时,因变量的增量就是边际量。边际分析法就是分析自变量变动1个单位时,因变量会变动多少的方法。
(1)边际需求。需求函数Q=Q(p)(p为价格)的导数Q′(p)称为价格为p单位时的边际需求。边际需求Q′(p)表示当价格为p时,价格上涨1个单位,需求量将改变Q′(p)个单位。

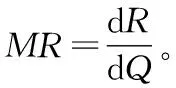
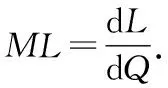
如果ML>0,即MR>MC,边际收益大于边际成本,表明在产量为Q时再生产1个单位产品多带来的收益增加量大于再生产1个单位产品多带来的成本增加量。这时,增加产出是有利的,可以使利润增加。
如果ML<0,即MR 如果ML=0,即MR=MC,边际收益等于边际成本,表明在产量为Q时再生产1个单位产品多带来的收益增加量等于再生产1个单位产品多带来的成本增加量。这时不再调整产量,利润达到最大,即实现了利润最大化。此时的产量为最佳生产量。 弹性分析也是经济分析中常用的一种方法,主要用于对生产、供给、需求等问题的研究。弹性概念用来定量描述一个经济变量对另一个经济变量的变化的相对反应速度。 一般情况下, 因Q=Q(p)为单调减函数,所以Ed<0.其经济意义:在价格为p时,如果价格提高或降低1%,需求由Q起,减少或增加的百分数是|Ed|。当|Ed|<1时,称需求是低弹性的;当|Ed|>1时,称需求是高弹性的;当|Ed|=1时,称需求是单位弹性的。 例:设某商品的需求函数为Q=100-10p,试求: (1)需求价格弹性Ed; (2)当p=2,5,6时的需求价格弹性, 并作出经济解释。 (2)当p=2时,Ed=-0.25,需求是低弹性的;而当p=2时,Q=40.这说明:在价格p=2时,若价格提高(降低)1%,需求Q将由40起减少(增加)0.25%。这时,需求下降(提高)的幅度小于价格提高(降低)的幅度。 当p=5时,Ed=-1,需求是单位弹性的;而p=5时,Q=25.这说明:在价格p=5时,若价格提高(降低)1%,需求Q将由25起减少(增加)1%,这时,需求下降(提高)的幅度等于价格提高(降低)的幅度。 当p=6时,Ed=-1.5,需求是弹性的;而p=6时,Q=20.这说明:在价格p=6时,若价格提高(降低)1%,需求Q将由20起减少(增加)1.5%.这时,需求下降(提高)的幅度大于价格提高(降低)的幅度。 经济领域中的任何函数都可类似地定义弹性,比如需求收入弹性、供给价格弹性等。 例:设生产某产品的边际成本为MC=3(万元/件),边际收入为MR=18-0.06x,若在最大利润的基础上再生产30件产品,利润会发生什么变化? 解:该产品的边际利润为 L′(x)=MR-MC=18-0.06x-3=15-0.06x 令L′(x)=0,即15-0.06x=0,得惟一的驻点x=250;所以产量为250件时,利润最大,在最大利润的基础上再生产30件产品,利润的改变量为 即最大利润的基础上再生产30件产品,利润会减少27万元。 例:已知某商品每周生产x单位时,总费用的变化率是f(x)=0.4x-12(元/单位),求总费用F(x)。 即销售x单位商品得到的总收入为R(x)=20x。 若现有a元货币,按年利率为r作连续复利计算,则t年后的价值为aen元;反过来,若t年后有货币a元,则按连续复利计算,现应有aen元,即资本现值。 纯收入的贴现值=总收入现值-总投资 例:若连续3年内保持收入率每年7500元不变,且利率为7.5%,问其现值是多少? 资本形成、收入预测都可以用这种方法计算获得。 为了研究经济变量之间的联系及其内在规律常需要建立某一经济函数及其导数所满足的关系式,并由此确定所研究函数形式,从而根据一些已知的条件来确定该函数的表达式。在数学上就是建立微分方程并求解微分方程。利用微分方程可以分析商品的市场价格与需求量(供给量)之间的函数关系,预测可再生资源的产量,预测商品的销售量,分析关于国民收入、储蓄与投资的关系问题等。 例:某年我国的国民生产总值(GDP)为80423亿元,如果我国能保持每年8%的相对增长率,问到11年后我国的GDP是多少? 解:建立微分方程:设第t年我国的GDP为P(t),t=0代表起始年。 偏导数也就是边际函数,它与一元函数的导数有着同样的经济意义。 例:设某一商品的市场需求受到商品的价格x与企业的广告投入y这两个因素的影响,其需求函数为Q(x,y)=6000-8x+50y+2xy-y2-x2。 就一元函数而言,需求的价格弹性是用来度量当价格变化时所引起的需求反应,即价格变动1%时,需求变动的百分数。对多元函数,同样也如此。 设有两种相关商品的需求函数为QA=QA(PA,PB)和QB=QB(PA,PB)。 直接价格偏弹性又称为自身价格偏弹性。 交叉价格弹性是度量某种商品对另一种商品价格变化而产生的需求的反应,对于两种和多于两种商品的需求之间关系的度量是有用的。 若EAB>0或EBA>0,说明两种商品是互相竞争的(或者互相取代的); 若EAB<0或EBA<0,说明两种商品是互相补充的。 因为A和B是“相互”的关系,所以只要EAB和EBA其中一项为正,即可判定是相互竞争的关系;同样,只要EAB和EBA其中一项为负,即可判定是相互补充的关系。 [1]侯风波.经济数学[M].上海:上海大学出版社,2010. [2]吴传生.经济数学——微积分[M].北京:高等教育出版社,2003. [3]卢达平.《微积分》在经济管理中的应用[J].龙岩学院学报,2006,(6):109~111. [4]杨丽贤,等.谈高等数学理论在经济领域中的应用[J].长春大学学报,2006,(12):20~22.2 弹性分析在经济分析中的应用
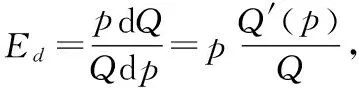
3 定积分在经济分析中的应用
3.1 已知边际函数或变化率,用定积分计算产量由a到b时原来函数的改变量

3.2 已知边际函数或变化率,用定积分求原来的函数

3.3 资本现值与投资问题


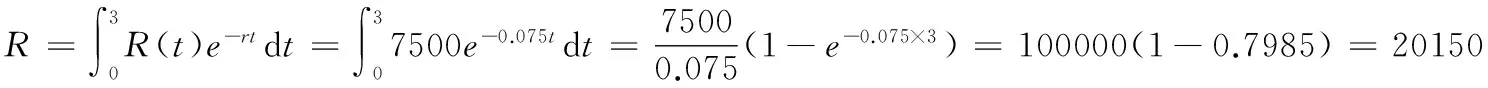
4 微分方程在经济分析中的应用
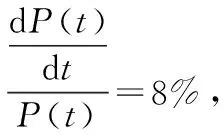
5 多元函数偏导数在经济分析中的应用
5.1 边际经济量
5.2 偏弹性



