浅析多元化数学的教育价值及其实现途径

陈 际 平，李 婷 婷

(陕西师范大学 数学与信息科学学院，陕西 西安 710062)

数学史是研究数学概念、数学思想和数学方法起源与发展的一门学科。数学史的内容极其丰富，它既是人类对数学知识的认知史，也是数学思想的发展史，同时还是数学发展与社会生产、科技、教育的关系史。随着新课程改革实践的探索和深入，数学史中多元化数学的教育价值受到了越来越多教育工作者和教育研究者的关注。将数学史引入课堂教育不单能激发学习兴趣，拓展数学认知面，并且能让学习者了解到多元化的数学，加深对中西方数学发展关联的认知，促进学习者思维的可持续发展。这也是使数学思维与世界数学前沿学科接轨，健全数学教育体系的途径。

一、数学史与数学文化

所谓文化，一般是指通过人的活动对自然状态变革而创造的成果，即一切非自然的、由人类所创造的事物或对象。文化既有人类生存的客观条件决定的客观性，也有人类生存的主观追求决定的主观性。[1]而数学作为一种描述客观世界的量化模式，受到客观世界的制约，具有明显的客观性，但数学对象终究不是物质世界中的真实存在，而是人类抽象思维逻辑推理的产物，是一种人为约定的规则系统，显然数学又具有主观性。因此，从这个特殊角度对数学进行分析，数学就是一种文化，即数学文化。[2]当然，数学文化作为人类文化系统中一个相对独立的子系统，它还具有区别于其他一般文化的特点，例如：它具有广泛的适用性、高度的抽象性和严谨性，以及以形式化、符号化和精确简洁为特点的数学语言等。

新一轮课程改革在课程的功能、结构、内容、乃至设置上发生了重要改变，人们希望能以课程改革作为突破口，进行一次全方位的教育改革，实现应试教育到素质教育的转变。[3]在数学课程上，此次改革就将数学文化与数学探究、数学建模一起作为重要内容，贯穿于整个新课程之中，并提出了“体现数学的文化价值”的基本理念。这里所说的数学文化价值主要指数学对于人们观点、精神以及思维方式的养成所起的重要影响。[4]怎样才能使数学文化有效地渗透到课堂之中，实现数学的文化价值？新课改决定将数学史引入课堂就是一种很好的方式。通过数学史展示数学发展的进程，让学习者了解到数学发展的客观规律，以及数学与人类社会发展之间的关系；通过数学史介绍古今中外数学家的奇思妙想和生活轶事，使学习者形成良好的逻辑思维品质，正确的数学观；通过数学史呈现多元化的数学思想方法，让学习者思维得到全面发展，学会站在前人的肩膀上以更广阔的视野看待人类的数学成就。在深化教育改革的今天，我们需要去开发、利用数学史，挖掘并实现数学史的教育价值，探索以数学文化价值为主导的数学教育，为世界数学的发展和传承贡献力量。

二、数学史中的多元化数学

数学从来就不是某一个国家、民族或个人的专利，不同时代，不同地域，不同民族之间的文化差异，都会给在其中探索发展起来的数学打上鲜明的文化烙印，形成多元化的数学。譬如，在东西方自古以来文化差异的作用下就形成了东西方两种不同的数学体系。正如白尚怒先生所说：“所谓东方数学，可以说是以中国数学为代表的数学，具有构造性、程序性、计算性、实用性的特点，从而成为了以计算为主的机械化倾向的数学体系；而西方数学，由古希腊发展起来继之以西欧数学，具有演绎性、抽象性、理论性、逻辑性的特点，继而成为以演绎为主的公理化倾向的数学体系。”例如，对同一个问题：“已知a、b、两数，求其比例中项。”从东西方数学的角度出发就会有两种不同的解法：东方数学会将此问题归结为“已知x2=ab求未知数x”的一个开平方运算的程序问题；而西方数学则会将其看作“已知线段a、b，求作线段x使上式成立”的几何作图问题，并在得出作法后证明其正确性。[5]

除了古代中国数学和古希腊数学以外，古埃及、巴比伦、古印度以及阿拉伯的数学也都有着各自的特点。下面我们就通过不同时期、不同地域的人们对一元二次方程求解，这同一问题上所使用的不同理论和方法，来体会数学的多元化特点。

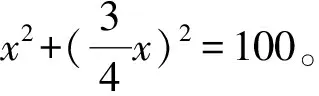
继这些古代文明之后，随着人类文化的发展与融合，各种数学思想、数学方法、数学形式等也相互交流、融合，但公理化思想和算法化思想在数学发展的历史长河中此消彼长，使数学的发展仍呈现出多元化的特征。例如，继漫长的中世纪黑暗之后的文艺复兴时期，古希腊数学重新引起了人们的重视，几何、代数都有了长足的进步，发展了数学自身的方法和理论，也大大推进了古希腊文化中的理性精神。而在十七世纪以后，社会和经济的巨大发展，促进了数学的快速进步。在这时期人们首先关注的不再是数学的证明方法和理论基础，而是它在生产技术和自然科学中的应用。特别是微积分产生初期，其问题解决和算法数学的倾向就十分明显。时至今日，现代数学已形成了众多类别、若干分支，并且呈现出它既是一门科学理论，又是一门应用技术的多元化特征。[8]

三、多元化数学的教育价值

数学史作为数学文化的重要载体，其教育价值一直是人们研究所关注的领域。在以前相关的研究中，研究的重点主要集中于数学史在激发学生学习动机、培养学生良好人格、扩宽学生视野等方面的作用。现在，随着这一领域研究的深入和丰富，数学史中多元化数学的教育价值日益被人们所察觉。研究认为数学史中多元化数学的教育价值大致有以下三点：

(一)理解尊重多元文化

在以往的课堂教育中，常常将数学史作为培养爱国热情与民主自豪感的材料，但我们认为还应该充分利用数学史中多元化数学，开展多元文化教育，让学习者从中感受到各地域、各民族间的文化差异，从而学会理解尊重多元文化。例如，通过对古代东、西方数学具体史料的学习，应领会到东方数学的实用性、计算性，西方数学的逻辑性、演绎性，并从中了解到东方“经世致用”的传统思想和西方所崇尚的理性精神。又如，结合历史思考可以得到，古埃及人之所以能够通过计算解决一元二次方程，而没有进行严格的演绎论证，是因为古代埃及的各种数学知识和计算方法多是为了解决尼罗河泛滥后土地的测量和食物的分配等问题，都是从日常生活中积累而来的，尚未形成完整的数学体系，它是数学源于生活的典范。而阿拉伯文明是在大量接受希腊、印度文化的基础上，迅速发展起来的，因此在阿拉伯数学中，我们既能看到希腊式的几何证明，又能看到东方式的计算技巧，是二者巧妙结合的产物。

其实，通过对多元化数学的学习，理解尊重多元文化并不是我们最终的目的，我们所希望的是在理解尊重多元文化的基础上，让学习者学会接受不同的优秀文化，汲取不同的文化精髓。试想一下，如果欧洲数学没有恢复希腊数学的思想，没有吸取中国数学的精华，怎能会有现今的如此强大。正是通过各区域、各民族文化、思想的融合与统一，才使得数学得到不断地发展，才使得人类文化得到不断地创新与进步。

(二)掌握不同思想方法

数学的思想方法作为数学知识的精髓，是对数学知识的高度总结与概括。这些概括性的知识潜移默化的作用于学习者的思维，不仅能发展他们的数学素养，还能促进他们学习迁移的形成。日本数学教育家米山国藏也说过：“即使学生把所教给的数学知识(概念、定理、法则和公式等)全忘了，铭记在他心中的数学精神、思想和方法却能使他受益终身。”但是，数学的思想和方法大都以抽象的形式存在，如何帮助学习者理解掌握，乃至应用这些思想和方法呢？我们认为数学史来自多元时空，多样化的问题解决方法以及简练严密的推导证明过程，正是学习者掌握不同思想方法的绝好机遇。

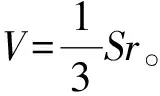
将不同数学家们所使用的具有数学美感与创新性的推导方法引入课堂，呈现在学习者面前，不单能丰富教学内容、开拓学习者认知数学世界的视野，最重要的是能让学习者了解到不同方法的思维过程，培养其全方位思维的能力，对推动世界数学的发展，以及科学技术的进步有着积极的意义。

(三)发展创造性思维

创造性思维，是思维活动的高级过程，是在个人已有经验的基础上，发现新事物、创造新方法、解决新问题的思维过程。[10]培养学习者的创造性思维是顺应社会发展的需要，是实现素质教育的要求。而不同时空、不同文化、不同数学家对同一问题的解决方法都具有其独特性与创造性，这能为学习者创造性思维的培养提供丰富的素材。以数学史作为突破口，把数学教育视为一种开发和培养智力的活动，而不仅仅是一些知识或方法的集合，将数学家创造数学真理的思维过程展现在学习者面前，在某种程度上可以改变从公式到公式，从定理到定理的教学模式，进而激发学习者的创造意识，培养创造性思维。[11]

例如，被开普勒誉为几何学两大法宝之一的勾股定理，至今已有四百多种证明方法，其中有不少方法就很巧妙。刘徽对勾股定理的证明使用了出入相补的原理，其在《九章算术》中对勾股定理的描述是：“勾自乘为朱方，股自乘为青方，令出入相补，各从其类，因就其余不移动也。合成弦方之幂，开方初之，即弦也。”古希腊的毕达哥斯(Pythagoras，公元前约569-约前500) 是勾股定理的最早证明者。据传毕达哥拉斯学派发现并证明了勾股定理之后，当即宰牛百头祭神，于是后人又称勾股定理为“百牛定理”。由于他的证明原稿已失传，人们推测他是通过将两个相同的正方形进行不同方式的切割来证明的。而欧几里得(Euclid，公元前330-前270)的证明方法是所有证明中最为著名的，希腊人称之为“已婚妇女的定理”，法国人称之为“驴桥问题”，阿拉伯人称之为“新娘的座椅”，在欧洲,又有人称之为“孔雀的尾巴”。除此之外，印度数学家婆什迦罗(Bhaskara，1114-约1185)则是使用了相似三角形对应边成比例的性质对勾股定理进行了巧妙的证明。

将数学史中的这些精妙的证明方法引入课堂教学，通过对同一问题不同解决方法的呈现，改变了学习者头脑中“正确答案唯一”的固有模式，发展求异思维，激发思维的多向性，引导他们突破常规，尝试从新的角度，新的途径寻求问题解决的方法。使学习者在数学学习中品尝到创造性思维的乐趣，从而喜欢数学，热爱数学，并进一步利用数学作为工具去有所创新、有所建树，推动科技和文化教育的进步。

四、多元化数学教育价值的实现途径

新一轮课程改革明确要求“数学史选讲”专题的内容必须反映出数学发展中不同时代的特点，并且我们也注意到教育部门所提供的参考内容中(早期算术与几何、古希腊数学、中国古代数学瑰宝、平面解析几何的产生、微积分的产生、近代数学两巨星、千古迷题、康托的集合论、随机思想的发展、算法思想的历程、中国现代数学的发展 )也涉及到了许多国家，不同时期的数学史实，这体现出此次课程改革对数学史中多元化数学教育价值的重视。那么如何才能在数学教育中体现出多元化数学，并且实现其教育价值呢？在此我们给出了三条基本途径供商榷。

(一) 系统介绍数学史知识，注重不同思想和文化的对比

系统的介绍数学史知识，可以使学习者了解到数学的主要分支，数学史上重大成果的发展和完善过程，中外著名数学家的重要贡献和人生经历,以及数学与人类社会的密切关系等。使得学习者拥有世界视野，并对数学学科的发展脉络有一个完整的认识，而不是仅仅停留在知道一些数学名人和几个历史命题的层面上。在系统介绍的过程中，引导学习者积极思考，对不同时期、不同国界的不同思想和文化进行对比分析显得尤为重要。

在内容的选择和编排上要以学习者的知识结构、心理需要为基础，实现趣味性、教育性与广泛性的结合，凸显数学的文化价值。譬如，可以选择几何学发展史，即“经验几何→演绎几何→射影几何→解析几何”的发展过程作为一个专题。在介绍时要重点突出不同时期几何学的不同特点。除此之外，在介绍经验几何时，通过讲解《九章算术》中以三角形的面积代替弓形面积的近似计算方法，让学习者了解到近似计算的起源和渐进过程，这也为现代数学引入计算机中用有限去表示无限的算法思想奠定了基础；在介绍演绎几何时，可以介绍几何作图的三大难题，开阔学习者的视野；而在介绍射影几何时，可以结合达·芬奇的《最后的晚餐》、拉斐尔的《圣母的婚礼》等画作，展现数学与艺术的关系，激发学习兴趣。

(二)渗透数学史内容，突出史料的多时空性

渗透数学史内容，是指以隐性的形式，根据教学需要，恰到好处的融入一些数学史知识，适时的介绍与所学内容有关的数学史材料，以激发学习兴趣，促进学习者对数学知识的掌握。而突出史料的多时空性，是指所选取的数学史内容应突破时空局限，力求反映不同时期、不同国度、不同民族、不同文化背景的数学历史。这样，通过对数学史的学习不单能更好地理解相关数学知识，而且还能体会到不同的文化、思想与方法，对今后的数学传承和发展奠定了坚实的基础。

例如，在等比数列求和公式的教学中，教师除了使用常见的错位相减法进行公式推导的演示以外，还可以向学习者介绍古埃及纸草书上有关等比数列的问题。这个趣味问题是一位妇人家里有七间屋子，每间屋子里有七只猫，每只猫捉七只老鼠，每只老鼠吃七棵麦穗，每棵麦穗可以长出七斗麦子。问屋子、猫、老鼠等各有多少，总数是多少？这其实是等比数列的求和问题，并且在纸草书上还写着2801×7 的算式，因此人们猜测古代埃及人可能已经总结出公比为7的等比数列前n项和的递推关系Sn=(1+Sn-1)×7。通过这段趣闻，可以引导学生将此递推关系推广到一般等比数列上，得到一般等比数列的求和公式。除此之外，还可以展示公元前三世纪，古希腊欧几里得的《几何原本》里利用比例性质推导得出等比数列求和公式的过程。通过来至古埃及和古希腊的两个公式推导方法的讲解，不单使学习者熟悉了等比数列的求和公式，而且还看到了关于这个公式推导的两种不同的思想方法。使学习者认识到数学并非枯燥无味，使其体会到学习数学的快乐，并建立生活中处处有数学的理念。

(三)开展探究性学习，体会数学史中的多元文化

探究性学习是此次课程改革大力推广的一种学习方式，即让学习者在创设的情景下，围绕着某个数学问题，自主探究、学习的过程。[12]在探究性学习中，教师只是组织者与指导者，而学习者需要在自己独立思考的基础上与他人积极合作，发现问题，提出问题，最后解决问题。探究性学习能使学习者主动的思考问题，加深对知识的理解，养成良好的学习习惯，培养其探索精神。因此对于数学史的学习也可以采取这种方式，可以给学习者提供来源广泛的数学史史料，并引导其观察分析这些史料，从中体会多元文化背景对数学的影响，探索不同的数学思想方法，猜测数学发展的规律等，并给出适当的解释或证明。数学史中有关各文明古国记数符号、计数系统与分数表示等的内容都可以作为探究性学习的素材，让学习者通过分析与探索发现各区域远古数学的渊源及各自数学的特点。除此之外，还可以通过对数学史上两大传世名著——《九章算术》与《几何原本》中经典题目的比较，让学习者体会算法倾向数学与演绎倾向数学的不同特点。

数学是人类文化的重要组成部分，其知识博大精深，奥妙无穷。数学教育不能单纯停留在数学理论的层面,而是要指导学习者对数学理论的实质进行深入探究，指引其体会依托于数学知识之上的数学思想和方法，领悟贯穿于数学研究活动中的科学精神和文化底蕴。我们借本文以“抛砖引玉”，希望引起更多数学教育工作者、数学教育研究者、数学教育爱好者对数学史中多元化数学的关注，共同探索实现其价值的有效途径。

[1]郝文武.多元文化发展中德育的终极关怀与多层面价值和方式——兼论当代中国德育哲学的变革[J].华东师范大学学报：教育科学版,2010,28(2):1-8.

[2]邹庭荣.数学文化欣赏[M].武汉:武汉大学出版社,2007:1.

[3]张迎春.高中新课程的几个转变[J].全球教育展望,2003,32(8):10.

[4]郑毓信,王宪昌,蔡仲.数学文化学[M].成都:四川教育出版社,2001:8.

[5]李文铭.数学史简明教程[M].西安:陕西师范大学出版社,2008:95-96.

[6]章勤琼,张维忠.多元文化下的方程求解[J].数学教育学报,2007,16(4):72-74.

[7]朱家生.数学史[M].北京:高等教育出版社,2004:8-45.

[8]项昭.数学史的多元文化价值及其应用——以高师校本课程《高中数学选修课程专题研究》开发为例[J].贵州师范大学学报：自然科学版,2008，26(3):6-10.

[9]汪晓勤,韩祥临.中学数学中的数学史[M].北京:科学出版社,2002:116-132.

[10]陈琦,刘儒德.当代教育心理学[M].北京:北京师范大学出版,2007:352-358.

[11]Fulvia Furinghetti. Teacher education through the history of mathematics [J]. Educational Studies in Mathematic，2007,66(2):131-134.

[12]中华人民共和国教育部.普通高中数学课程标准:实验稿[M].北京:人民教育出版社,2003:98-101.