基于多种方法的共同配送成本分配模型研究
2011-01-16琚春华高春园鲍福光蒋长兵
琚春华,高春园,鲍福光,蒋长兵
(浙江工商大学 信息学院,浙江 杭州 310018)
基于多种方法的共同配送成本分配模型研究
琚春华,高春园,鲍福光,蒋长兵
(浙江工商大学 信息学院,浙江 杭州 310018)
共同配送是一种经长期探索发展而产生的追求配送合理化的新物流模式,这种物流整合所产生的共同效益的分配是共同配送的关键。通过分析共同配送的社会经济效益和共同配送利润分配 (成本分摊) 的模型及有效求解方法,运用 Shapley 值法、最小核心法、最小核心多目标规划法、GQP 法、简化的 MCRS 法和纳什谈判模型等有效分配方法对共同配送问题进行求解,并进行对比分析。
共同配送;成本分配;Shapley 值;最小核心;GQP;MCRS
近年来,共同配送在国外得到了迅速发展。例如,日本福冈市滕井区的共同配送系统;德国不来梅市的共同配送体系;摩纳哥的共同配送系统等[1]。在我国,尽管共同配送的发展已经引起了广泛关注,但是还处于起步阶段;对共同配送的研究取得了一定的成果,但是尚处于探索阶段,还需要进一步深入研究。
我国的物流企业大多数为中小型企业,企业的整体实力和财力较弱,缺乏必要的资金、设备和专门人才,无力单独自建物流系统。因此,需要利用共同配送模式来解决现有物流模式的不足。从目前运作情况看,很多物流配送公司的业务操作主要存在以下特点:同类产品比较集中,主要是小型物件;单次定单量较小,属于多批次少批量类型;商场、超市配送量占很大比重;车辆来源全部或部分从社会租用,包括长期合作和临时采购;不同客户的配送区域不同,覆盖面不同。为了有效地提升利润空间,提高配送时效和客户满意度,诸多物流企业一直在寻求通过共同配送的方式来解决,但从目前实施情况看,效果不是很明显。
实行共同配送可以降低物流成本,提高物流效率,增加企业的经济收益。基于企业合作的共同配送能够带来更大的经济效益,但是共同配送一直得不到较大的发展,关键原因在于共同配送所产生的“共同经济效益”无法在合作的企业之间进行合理的分配。在此运用博弈论思想,通过建立博弈合作费用分摊模型,确定各企业在共同配送中所分摊的费用和利润分配。
1 共同配送的社会经济效益
共同配送可以给企业和社会带来不同程度的社会和经济效益。从微观角度讲,企业可以实现配送作业的经济规模,提高物流作业效率,降低企业运营成本,节约企业资源,减少固定资产投资,减少配送车辆无效里程,促进企业集中核心业务,扩大市场覆盖面和销售网络,提高市场份额等。从社会角度讲,可以节约货物在途时间,减少环境污染,减少车流总量,改善交通状况,提高车辆装载率,节省物流处理空间和人力资源等效益。
共同配送在充分发挥企业人、财、物、时间等物流经营资源最大效率的同时,可以促进物流服务效果及社会效益的提高。
2 共同配送利润分配 (成本分摊) 的几种模型及有效求解方法
将多方合作的共同配送思想与利润分配问题联系起来,使得共同配送这种高效的物流模式能够在现实中广泛应用。目前有以下几种模型及有效分配方法。
2.1 二次分配法
二次分配法首先直接分摊部分费用 (如边际费用或可分费用),再根据某项数量指标分摊剩余费用。该方法中最典型的是可分费用剩余效益法(SCRB法)。SCRB 法基于以下思路:联合费用的分摊“或多或少”地要按照使用者的支付意愿比例分摊,“或多或少”因素的引入是由于按照比例费用分摊法的使用仅仅是当第一次分配完使用者的边际 (或可分费用) 费用以后,才开始采用使用者支付意愿的比例减去已经分配的边际费用这种标准[2]。
2.2 Shapley值法
Shapley 认为“分配合理”的假定是:①每人的分配数与被赋予的记号数无关 (对称性);②若成员对所参与的合作没有贡献,则不应该在合作总获利中分得利益 (有效性);③各成员在全体合作效益中获得的分配数之和应等于合作总效益数 (总和性);④各成员的总分配数应是所参与合作的分配数之和(可加性)。
根据以上4条假设,从逻辑上证明了Φi(v) 是唯一有解的,这个解的模型是:
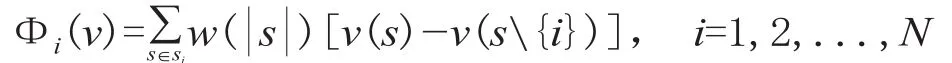
式中:Si为包含 i 的所有子集的集合;s 为 Si中的任意元素 (含 i 的子集)。
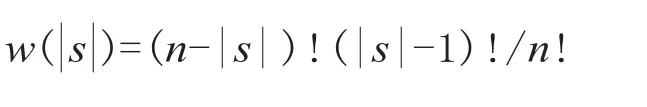
式中:|s|为集合s中的元素个数;w(|s|)为加权系数[3]。
2.3 简化的MCRS(Minimum Cost-Remaining Savings)法
首先确定分配向量的上、下界向量Xmin≤X≤Xmax,其中Xmax=(u1,u2,…,un),Xmin=(l1,l2,…,ln),然后由点 Xmax和 Xmin连 线与超平面 ∑nx=C (N) 的交点 X*作为解值,即
i=1i由 Xmin+λ (Xmax-Xmin)和xi=C (N) 联立约束求解,可得 (λ, X*)。通常在 MCRS 方法中分配向量的上下界 Xmax和 Xmin是通过求解线性规划问题求出的,而在简化的 MCRS 方法中,则直接定义 Xmax=U, Xmin=C (N)-C(N-{i}), ∀i∈N,即将各个成员的应该投资费用和理想分摊费用分别作为其最高和最低的分摊投资费用[4]。
2.4 核心法
核心法 (Nucleolus法) 是 Gillies[5]于 1953 年提出的一个合作对策的解概念,不被任何分摊方案优超的分摊方案的集合,换句话说,核心中的每个分摊方案都能够被任何联盟所接受。按照这一基本思想,一个合理的分摊方案 x=(x1,x2,…,xn) 应满足以下条件:

x=(x1,x2,…,xn) 的全体称为核心,记为C(v)。
实际应用中,由于联盟应分摊的费用与总费用常出现相互矛盾的情况,核心C (v) 有可能是空集。最小核心法是解决这类问题的一种方法,其数学模型为:
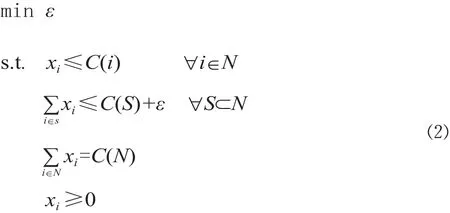
ε 的含义是在联盟的分摊费用和总体费用出现矛盾的情况下,为了使所有成员都能参与大联盟而向每一个小联盟或成员征收的附加费用,目标是附加费用最小化。
2.5 最小核心多目标规划法
由模型(2)可以发现,将合作费用C(S) 尽少量增加且增加量均相同,这种作法只是追求数学算法上简单性的需要,但“公平性”有所欠缺,也失去了联盟分配的合理性原则。将各联盟费用C (S) 的增加量以不同数值进行增加,换言之,考虑各成员不同的具体情况,向每个成员征收不同的附加费用[6]。
考虑将模型(2)中的联盟费用C (S) 增加不同的增加量εj( j=1,2,…,m),m 是除去空集和大联盟N的所有联盟的个数。目标函数 minεj( j=1,2,…,m)表示对各联盟费用C (S ) 的增加量 εj尽可能的小。xi为决策变量。可以得到如下最小核心的多目标规划模型[6]:
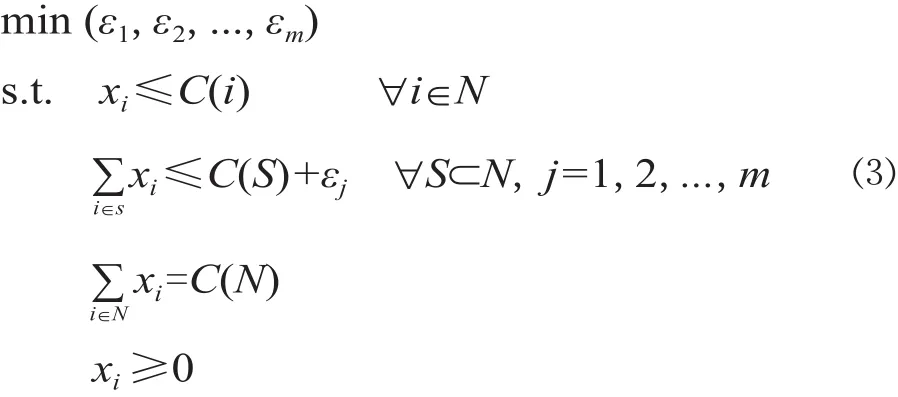

多目标决策问题的绝对最优解是不常见的,最多的是有效解 (x*,ε*),也称 Pareto 最优解。多目标决策问题的有效解可能会随着处理方式的不同而有所差异。
2.6 GQP(Game Quadratic Programming)方法
使用二次规划方法 (QP) 计算出“最优”分配方案。目标函数 min Z=(x−v)2是使得各个成员的分ii摊数目与理想分摊量之差额最小。这种做法是各个成员都能够认同的做法。约束条件是各个成员分摊的数都小于单独建站的费用,并且各个成员的费用之和也都小于彼此组合的费用[2]。即求解模型(6)线性规划问题:

式中:C (S) 为参加分配的局中人形成联盟 S 时的费用;C (N) 为全体局中人形成大联盟时的总费用;vi为第 i 个成员最少需要承担的费用 (理想分摊量),即可分离费用,可分离费用可以表示为=c (I )−c (I−i);i=1,2,...,n;c (I-i) 为成员 i 没加入时的总费用;c (I ) 为项目的总费用,i=1,2,…,n,为全体成员的集合。
2.7 纳什谈判模型
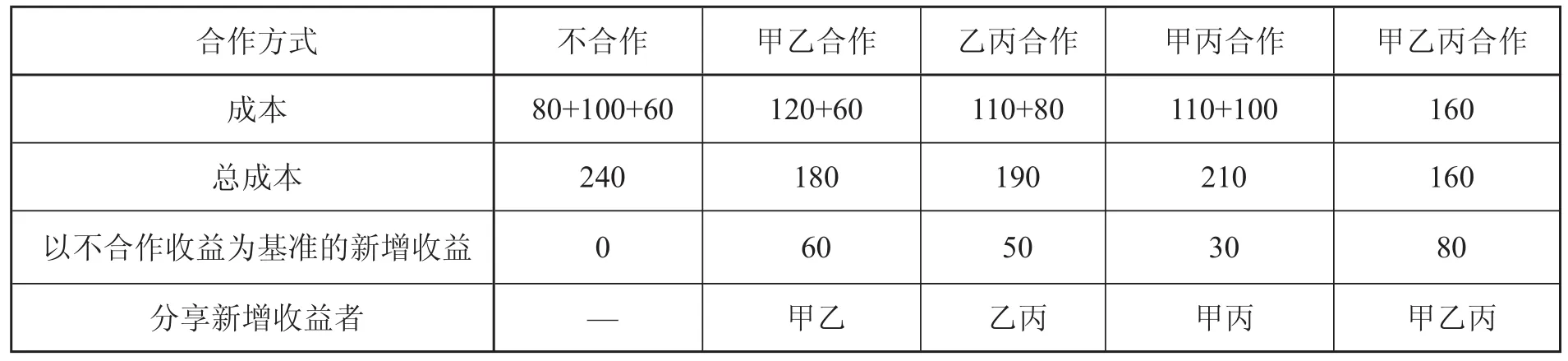
设有 n 个企业的集合N=1,2,…,n,并且用 n 维空间的一个闭凸子集 F 表示一个可行效用的支付向量集。令C={c1,c2,…,cn},为各企业单独开展配送所需的费用,X={x1,x2,…,xn},为各企业开展共同配送时分摊的费用,有xi−C (N) =0,0 因此,通过求解下面的非线性规划问题[2]得到 X。 多家企业合作实现共同配送,需要探讨以下几个问题:①虽然每个客户的配送区域和线路不完全统一,但可以从大多数客户重叠的线路中开始实现共同配送;②配送运量相对比较集中和稳定的线路,完全可以签订一批固定车辆进行操作,这样有利于利润及运作时效和服务质量的稳定;③通过和现有客户沟通扩大合作线路,以达到规模化运作,从而实现共同配送。 问题假设:①有甲乙丙3家配送企业,分别向ABC 处配送货物,企业之间的运送成本如图1所示;②3 家配送企业的货物运输量之和不大于车辆的载重量。 在不考虑车辆启用费和司机等费用减少的情况下,在单独配送时,每一方各获利0单位。甲乙合作,可获利60单位;甲丙合作,可获利 30 单位;乙丙合作,可获利50单位。当甲乙丙三方合作时,则可获利 80 单位。共同配送的利润分配见表 1。如何合理分配 80 单位收益成为共同配送的关键。 为了建模方便,用数学符号把问题形式化。记N={1,2,3},式中,1,2,3 分别为甲、乙、丙的数字代码,N 的各个子集合 (含 N 本身) 代表各种合作方式。例如,{1,2}表示甲乙合作方式,{2,3}表示乙丙合作方式,N={1,2,3}表示三方合作方式。定义在 N 的全体子集上的函数 (称为集合的特征函数)为v (.),表示相应合作方式下的获利数。如 v({1,2})=60,即甲乙合作,获利 60 单位;v({1,3})=30,即甲丙合作,获利 30 单位。记三维向量φ (v) = (φ1(v),φ2(v),φ3(v)),式中,φi(v) 表示参与者 i (i=1,2,3) 在3人共同合作总获利中应该分得的利益数。 表1 共同配送的利润分配 运用 Shapley 值法、最小核心法、最小核心多目标规划法、GQP 法、简化的 MCRS 法和纳什谈判模型等有效分配方法对共同配送问题进行求解比较分析。 3.2.1 Shapley值法 应用 Shapley 值法,3 人合作问题分配利益如下。对甲而言,φ1(v) 的计算如表2所示。 表 2 φ1(v) 的计算过程表 同理,对乙的总分配数 φ2(v)=0×1/3+60×1/6+50×1/6+50×1/3=35。 对丙的总分配数φ3(v)=0×1/3+30×1/6+50×1/6+20×1/3=20。 甲乙丙合作,实行共同配送情况下的收益与成本如表3所示。 其他的方法 (如最小核心法、最小核心多目标、GQP 法、简化的 MCRS 法和纳什谈判模型等)都可以用求解线性规划的计算软件求解。 3.2.2 最小核心法 利用最小核心法,该问题的数学模型为: 利用 lingo 求解得X*=(56.667,56.667,46.666) 3.2.3 最小核心多目标规划法 根据模型(3)的求解方法,3个子目标的隶属度函数分别为:μ(ε1)=(60-ε1)/60=1-0.016 7ε1,μ(ε2)=(30-ε2)/30=1-0.033 3ε2,μ(ε3)=(50-ε3)/50=1-0.02ε3。 根据公式(4),建立如下规划方程: 3.2.6 纳什谈判模型 该问题的纳什谈判模型为: 应用计算软件求解纳什谈判模型,可以得X*=(53.3,73.3,33.4)。 应用 Shapley 值法、最小核心法、最小核心多目标、GQP 法、简化的 MCRS 法和纳什谈判模型等分配方法求解得到的结果如表4所示。 表4 各种分配方法的分配结果 比较上述6种方法可知,不同的分配方法得到的结果不同。采用最小核心法和 GQP 法求解结果一样 (本例巧合,实际上这两种方法也比较接近),各方支付较为平均;采用简化的 MCRS 法、Shapley 值得出的结果比较接近,优势方支付较少,并且在同样的条件下,Shapley的4个假设条件比较现实地体现了公平性原则,其计算结果与每一个成员在任何子联盟中获得的利益不会比在全联盟中得到的更多的原则向吻合,满足了理性人普遍接受的合理性规则。在实际应用中,Shapley 还可以针对不同的情况,对各个合作者赋予不同的成本利益分配权重,以便使分配更为合理;采用最小核心多目标法进行求解可以避免出现空解集。纳什谈判模型易操作,并且适合于合作企业实力相当、运营成本相近的情况,其中无限次重复博弈为企业实现长期且高效率的合作提供了可能,单独配送与共同配送成本比较如表5所示。从计算方法上考虑,除了 Shapley 值法,其他的方法都可以用求解线性规划的计算软件,易于求解。通过借助于现代智能计算机,利用相应的数学计算软件或统计分析软件,可以得到相应的可用解集。 表5 单独配送与共同配送成本比较表 “公平”是分配原则的核心。只有“公平”才能保证各个成员共同参与项目建设,而公平地分配费用也是刺激各个成员和团体间进一步合作的动力。因此,公平可以看作是检验分配方案合理与否的方法。由于每种分配方法各有利弊,在竞争激烈的市场经济时代,特别是网络经济时代,选择合适的合作伙伴及合理的成本利益分配方法对企业未来发展异常重要。 [1] 贺政纲,廖 伟. 共同配送国内研究综述[J]. 商业时代,2009 (5):21. [2] 徐向阳,安景文,王银和. 多人合作费用分摊的有效解法及其应用[J]. 系统工程理论与实践,2000,3(3):116-119. [3] 姜启源. 数学模型[M]. 北京:高等教育出版社,2003. [4] 陈文颖. 大气污染总量控制规划方法与智能决策支持系统[D]. 北京:清华大学,1996. [5] Gillies D B. Solutions to general non-zero-sum games[C]//Tucker A.W,Luce D. R:Contributions to the Theory of Games.Princeton,N.J:Princeton University Press,1959:47-85. [6] 熊国强. 多人合作费用分摊的多目标规划解法[J]. 运筹与管理, 2006,15(1):13-17. [7] 李荣钧. 模糊多准则决策理论与应用[M]. 北京:科学出版社,2002. [8] 李坤杰,陶跃钢,刘国平. 非线性极大极小系统全局优化算法的分析[J]. 数学的实践与认识,2008,38(20):127-133. [9] 普拉伊特 K 杜塔. 策略与博弈:理论及实践[M]. 上海财经大学出版社,2005. Study of Cost Allocation Model of Common Delivery Based on Multiple Methods JU Chun-hua, GAO Chun-yuan, BAO Fu-guang, JIANG Chang-bing (Information School, Zhejiang Gongshang University, Hangzhou 310018, Zhejiang, China) Common delivery is a new logistic mode which has been developed in long term to make logistic delivery more rational. Allocation of the common bene fi t generated by the logistic integration is a key element of common delivery. By analyzing the social and economic benefit of common delivery and model and effective method of benefit allocation, many effective allocation methods,including the Shapley value method, minimum core method, multiple targets planning method, CQP method,simpli fi ed MCRS method and the Nash negotiation model,are used to find solution of common delivery problems.Comparative analysis is made as well. Common Delivery; Cost Allocation; Shapley Value; Minimum Core; GQP; MCRS 1003-1421(2011)02-0057-07 F252.3 A 2010-08-09 国家自然科学基金(71071141);浙江省自然科学基金重点项目(Z1091224);浙江省自然科学基金资助项目(Y6090015);教育部省部共建人文社会科学重点研究基地“浙江工商大学现代商贸研究中心”资助项目(09JDSM25YB) 责任编辑:宋小满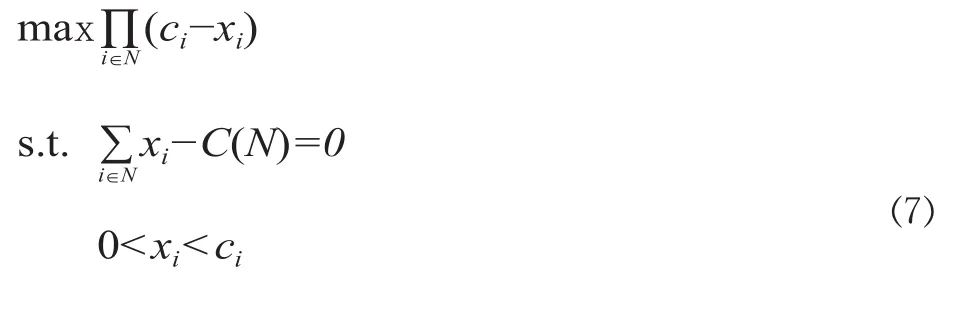
3 实例分析
3.1 共同配送的假设与数学模型
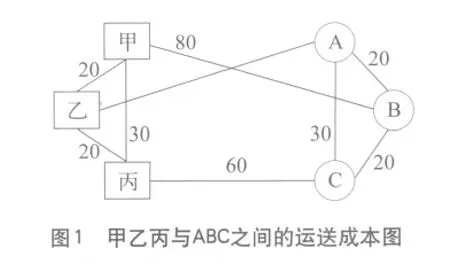
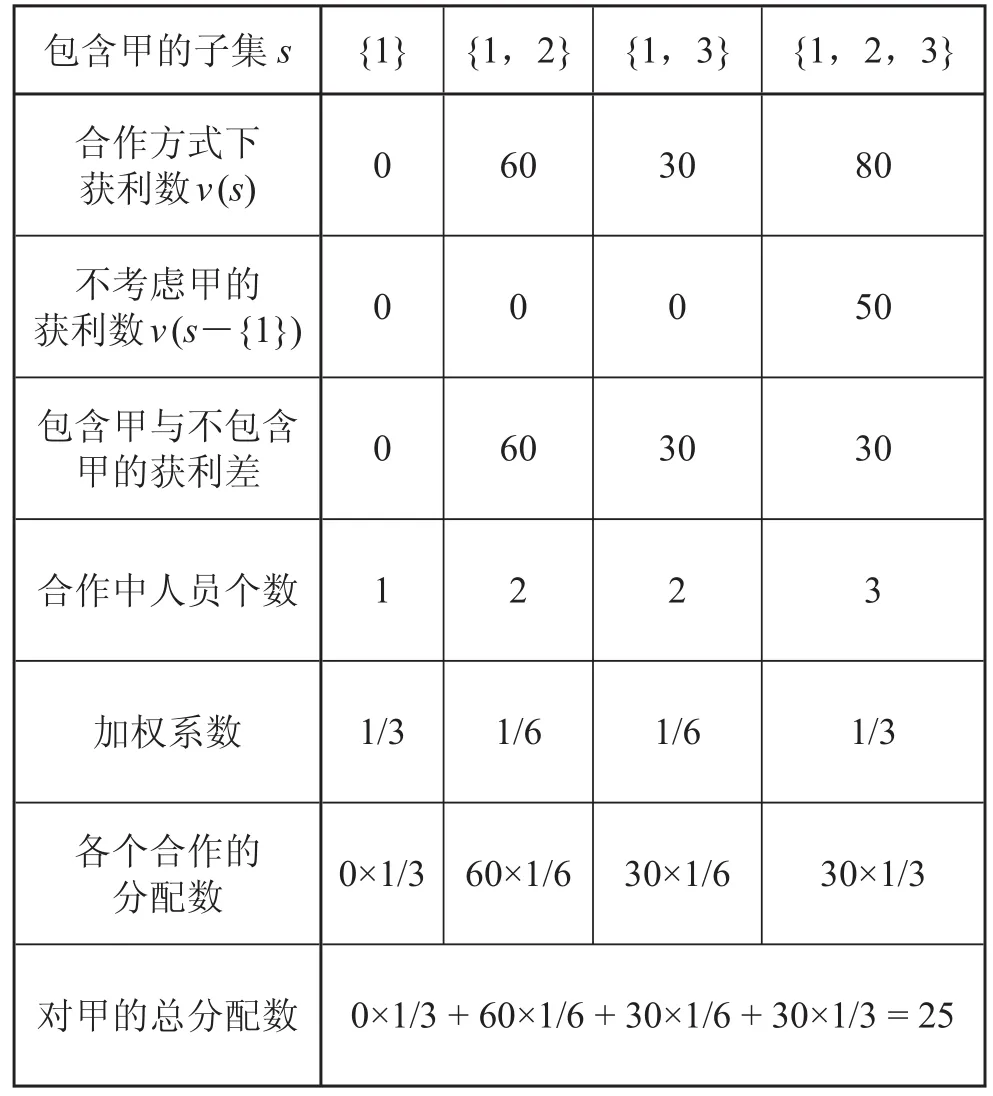
3.2 各分配方法比较

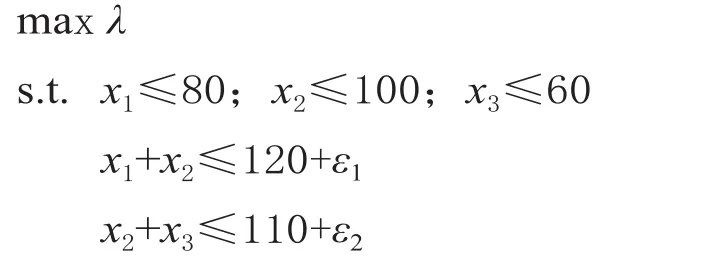

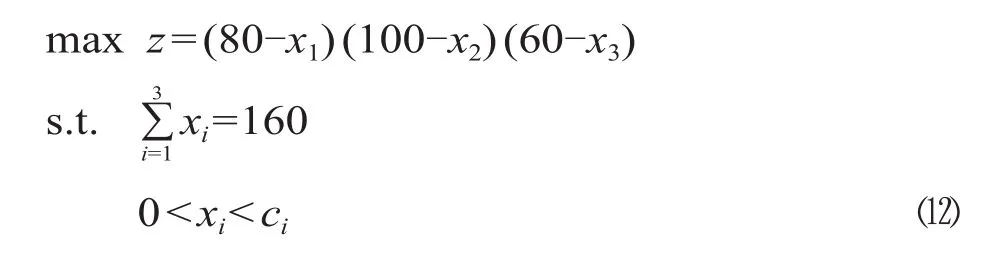
3.3 分配方法的比较
4 结束语
