一维型材合理下料的数学模型

李 明

（苏州工业职业技术学院 公共教学部，江苏 苏州 215104）

一维型材合理下料的数学模型

李 明

（苏州工业职业技术学院 公共教学部，江苏 苏州 215104）

一维型材合理下料问题的解决是多维下料问题优化的基础。从模型建立的角度出发，以材料利用率高达97.84%为目标，用非线性规划模型Ⅱ改进整数规划模型Ⅰ，解决整数规划模型Ⅰ中人工枚举下料方案而导致的决策变量偏多的问题，减少生产过程的复杂性，降低生产成本和管理成本，提高切割方案的生成速度。非线性规划模型Ⅱ解决了多种型材下料问题的最优化，使企业效益达到最大化。

一维型材；优化下料；整数规划；非线性规划

1 相关研究背景及问题的提出

所谓“下料问题”就是把规格相同的一些原材料进行合理分割后再组合，确定切割下来材料的排样方案，以达到材料利用率最高。这类问题可分为三大类：切割问题（Cutting Stock Problem）、排样问题（Assortement Problem）和装箱问题（Bin Packing Problem）。切割问题如棒材或型材的下料，在造船业、建筑业中钢筋、铝合金、圆钢的下料，以及家具制造业中板材的下料；排样问题如印刷业中书刊、报纸的排版或电子工业中集成电路的排布问题；装箱问题如物流行业中集装箱载物时，将货物装入有限空间的排布等[1]。优化下料问题，可以最大限度地节约资源，降低生产成本，提高企业的竞争力，给企业带来直接的经济效益，因而对一维型材下料问题的研究具有重要的现实意义和应用价值。

目前，国内外在优化下料问题的研究上，较多是从算法改进的角度上进行的。如文献[2]针对原材料利用率最高的切割方式优先选择策略，设计了贪心算法；文献[3]针对大规模一维型材下料问题很难找到最优解，设计了启发式算法；文献[4]针对各算法容易陷入局部最优的缺点，采用了自适应广义粒子群优化算法来达到优化的高效性。此外，还有遗传算法、模拟退化算法、蜂群遗传算法等。倘若从模型建立的角度出发，用科学的方法取代人工筛选，降低工人的工作量，减少企业成本，提高材料利用率，那么也是一种有效解决问题的好思路。以下从典型实例出发进行探讨和研究。

如某单位需要加工制作100套工架，每套工架需要用2.9m、2.1m、1.5m的圆钢各一根。已知原材料长7.4m，问如何下料才使得所用的原材料最省？

2 问题的分析

如果按照单一截材方案，将一根7.4m原材料切割为2.9m、2.1m、1.5m的型材各一根，最后余料是0.9m，小于原材料中尺寸规格最小的1.5m，那么生产100套这样的工架，最后余料总和为90m，材料利用率只有87.84%，并造成一定量的浪费和生产成本的增加。因此，以余料最少或使用的原材料最省为目标，针对7.4m长的原材料，排列出所有切割可能性的8种方案（见表1）。

表1 一根7.4m原材料切割的8种方案m

3 模型的建立与求解

设决策变量为xi，代表第i种方案下使用原材料的数量，i=1,2,…,8；目标是切割下来的余料最少或使用的原材料最省；约束条件是切割出来的型材需求量都是100根，故可以建立如下的整数规划模型Ⅰ。通过LINGO9.0软件实现过程如下：

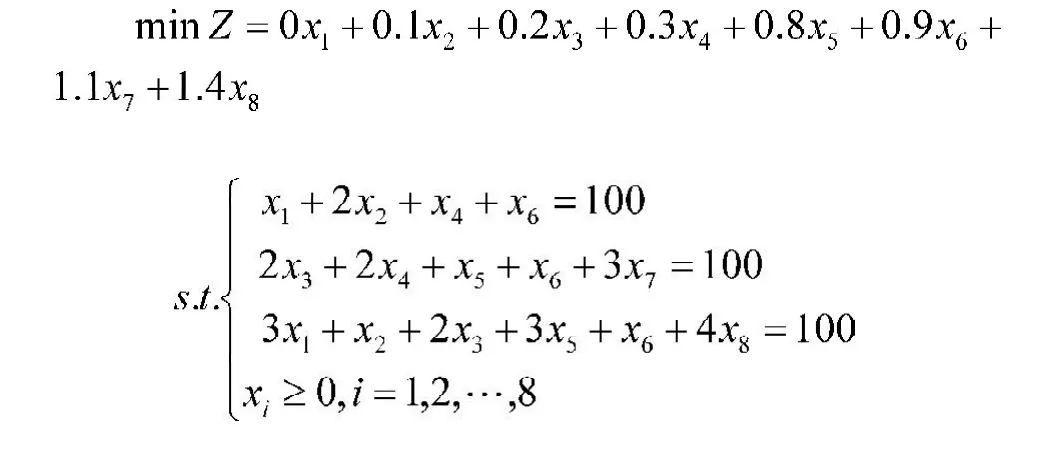
!建立数据段，确定各方程的系数矩阵和常数项矩阵的数据;

通过LINGO9.0软件计算得到求解报告，如图1所示。经过6次迭代得出余料最少为16m，切割方案为：第2方案截取40根，第3方案截取30根，第4方案截取20根，原材料合计使用了90根，就能完成整个任务的要求。此时原材料的利用率为97.84%，比单一截材时的利用率提高了10%。

如果以原材料使用最省为目标，那么目标函数应该为：

在其他的约束条件不变的情况下，得到的是同样的结论[5]。

4 对整数规划模型Ⅰ的再思考

整数规划模型Ⅰ固然好，但排列出所有的切割方案需要时间、人力和物力，当型材规格较多或原材料类型较复杂时，采取整数规划模型Ⅰ会无形间加大工人工作量，增加生产工序的复杂性，降低工作效率。从表1余料的数据结果以及最优化后8种方案选中3种，表现出两个较为突出的问题，成为对整数规划模型Ⅰ进行改进的突破口。

问题1：假如从7.4m原材料中各截取2.9m、2.1m、1.5m的型材各一根，剩下的余料是0.9m，那么8种方案中余料比0.9m少的，对提高利用率无意义，因而不予考虑，这样就将8种方案浓缩为5种备选方案（见表2），也就是将变量由原来的8个减少到5个。

据此，将整数规划模型Ⅰ更改为：

图1 整数规划模型Ⅰ的求解报告

表2 一根7.4m原材料切割的5种方案m

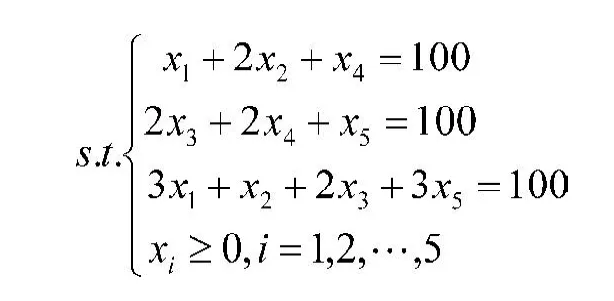
在其他的约束条件不变的情况下，依据更改后的整数规划模型Ⅰ会得到与前面同样的结论。

问题2：假如原材料类型较多，需要的型材规格也比较多样的时候，采用枚举的方法工作量比较大，而且生产部门采用不同的切割模式越多，越会导致生产过程的复杂化，从而会无形增加生产和管理成本。整数规划模型Ⅰ虽有8种方案，但优化过后仅选择了其中的3种方案，由此以切割方案的选取不超过4种为原则，可以降低生产和管理成本，建立更为便捷、合理、科学而高效的数学模型[6-10]。

5 对整数规划模型Ⅰ的改进

评判一个好的下料模型，首先考虑的是提高原材料的利用率；其次要求切割方案尽可能少。因而在切割方案不超过4种的原则下，增设决策变量，表示第i种型材使用第j种切割方案时的数量；xi仍然代表第j种方案下使用原材料的数量，目标是切割下来的余料最少或使用的原材料最省；约束条件是切割出来的型材需求量都是100根，同时余料应该小于型材中的最小尺寸1.5m，故可以建立如下的非线性规划模型Ⅱ[11]。

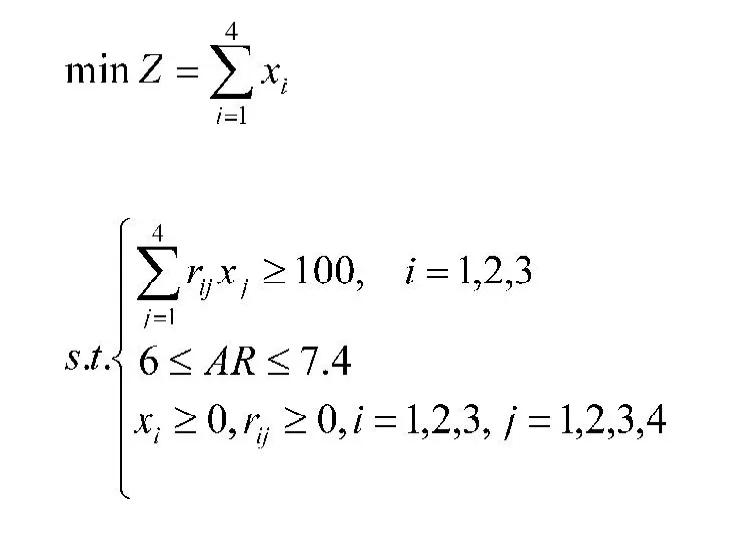
其中，型材矩阵为A=(2.11.52.9)，切割方案矩阵为R=(rij)3×4。由于4种方案的排列顺序无关紧要，可在程序运行时增加约束条件，以缩小变量搜索的时间，减少程序运行时间。

通过LINGO9.0软件实现过程如下：

!建立集合段，确定各量的下标;

!建立数据段，确定各方程的系数矩阵和常数项矩阵的数据;

通过LINGO9.0软件计算得到求解报告，如图2所示。经过5924次迭代，解得最省的原材料需要使用90根，余料总和为16m，原材料的利用率仍为97.84%，同时得到切割方案（见表3）。其中方案2和方案4切割方式相同，可整合为表4。与整数规划模型Ⅰ结论相比，证实了非线性规划模型Ⅱ的可行性。

图2 非线性规划模型Ⅱ的求解报告

非线性规划模型Ⅱ的最大优势是：在保证和提高原材料利用率为97.84%的情况下，增设了切割方案下型材使用的数量为变量，解决了整数规划模型Ⅰ由人工枚举方案而导致的决策变量偏多、工作量较大的问题。为精简生产过程，降低生产成本，加快切割方案的生成速度，提高企业排样效率，寻找到了一种合二为一解决问题的思路和方法，为多种型材下料优化模型奠定了基础。

6 结束语

下料问题随着实际情况的不同，约束条件会有所变化，但无论条件怎么改变，一定要注重对问题做层层深入的分析，对模型进行不断改进，使得模型具有更加广泛的通用性。非线性规划模型Ⅱ及LINGO程序的求解方法，不但具有较好的通用性，而且能够实现较大规模一维型材下料优化问题，使企业效益达到最大化。

表3 一根7.4m原材料切割的4种方案 根

表4 合并表3中的方案2和方案4根

[1]胡玉珠.一种型材优化下料方法的研究与应用[D].长春:长春理工大学，2009.

[2]陈炼，马永生，刘光明.一维下料方案的贪心算法优化[J].南昌大学学报:工科版，2005，27(4):71-73，84.

[3]刘蓉.一维下料问题的一种启发式算法及其应用[D].合肥:合肥工业大学，2006.

[4]沈显君，杨进才，应伟勤，等.一维下料问题的自适应广义粒子群优化求解[J].华南理工大学学报:自然科学版，2007，35(9):113-117.

[5]代西武，李美娥.线材合理下料的数学模型[J].北京建筑工程学院学报，2005，21(2):61-62.

[6]刘睿，严玄，许道云，等.一种有效的求解一维下料问题的启发式算法[J].计算机应用，2009，29(4):1180-1181，1187.

[7]沈飞，陈杰，陈峰.循环取料下的多道口分配问题及其算法研究[J].物流技术，2009，28(9):46-48.

[8]王建，闫立梅.型材下料表的参数提取和管理[J].计算机辅助工程，2008，17(3):65-68.

[9]王连杰.基于线性规划的一维优化下料系统研究与开发[D].大连:大连理工大学，2003.

[10]韩中庚.实用运筹学——模型、方法与计算[M].北京:清华大学出版社，2007:12.

[11]孙晓雅.整数非线性规划方法优化下料问题[J].机械工程师，2006(10):100-101.

Mathematical Model of Rational Cutting of One Dimensional Profile

LI Ming
(Public Courses Department, Suzhou Institute of Industrial Technology, Suzhou,215104,China)

The solution of the rational cutting of one dimensional profile lays the foundation for solving the issue of multidimensional cutting. From the view of model building, this article, setting a goal of97.84% of material utility, uses the nonlinear programming model II to change the integer programming model I, which solves the extra decision variable caused by the enumeration in integer programming model I, decreases the complexity of the working process, reduces the cost of production and management and improves the speed of cutting plan. The nonlinear programming model II optimizes the issue of multidimensional cutting and enterprises can gain the highest profit.

One dimensional profile; Cutting Optimization; Integer programming; Nonlinear programming

O224

A

1671-4326(2011)04-0056-05

2011-10-31

李 明（1975—），女，新疆石河子人，苏州工业职业技术学院公共教学部讲师，硕士.

乔维德]