碳基复合材料有效性能的细观力学研究

周振云，胡耀华，马 李

（台州学院 物理与电子工程学院，浙江 台州 318000）

碳基复合材料有效性能的细观力学研究

周振云，胡耀华，马 李＊

（台州学院 物理与电子工程学院，浙江 台州 318000）

作为一种多相体材料，碳基复合材料的力学性能和损伤破坏规律与其组元材料的弹性常数、体积含量以及细观结构密切相关。独创了组元材料试样加工与拉伸试验方法，获得了石墨基体和碳纤维的拉伸模量、强度和断裂应变率，在此基础上利用细观力学中Eshelby等效夹杂理论和Mori-Tanaka方法，建立了预报材料弹性常数的细观力学模型，并将理论预报结果与试验结果进行了比较，分析了误差产生的原因。结果表明：理论预报值与试验值之间的误差在10%以内，说明计算模型合理，计算结果可信。

碳基复合材料；组元；拉伸试验；细观力学

1 引言

碳纤维增强碳基体复合材料具有高比强度、高比模量、耐疲劳、抗摩擦性能、高温下仍能保持高强度、良好的耐烧蚀性能及结构尺寸稳定、可设计性强等特点，受到航空航天领域的广泛关注［1-3］。

作为一种多相体材料，碳/碳复合材料具有强烈的结构特征，其力学性能和损伤破坏规律与其组元的弹性常数、体积含量及细观结构密切相关。因此针对组元进行力学试验，获得可靠试验数据，分析复合材料各组成相的力学性能与复合材料宏观力学性能之间的关系是正确预报碳基复合材料性能和建立力学模型的关键［4-6］。

本文针对碳/碳复合材料的特点，设计并完成了对组元材料的性能测试，在获得相关性能参数的基础上，引入细观力学研究方法，以Eshelby等效夹杂理论和Mori-Tanaka法建立预报模型，对细编穿刺碳基复合材料的常温下的弹性模量及泊松比进行了理论预报，并将理论预报结果与试验结果进行了比较。

2 实验

2.1 试样设计

成品纤维束不同于原始纤维束。碳纤维束在穿刺以后，要经过浸渍、碳化、石墨化复合工艺等高温、高压和化学处理过程，会引起纤维本身的结构变化，产生机械损伤，对碳纤维束性能带来不利影响，因此要单独获取与成品细编穿刺碳/碳复合材料中的纤维束性能相同的纤维束是不实际的，只能从成品材料中分离出纤维束。

试样设计考虑以下几个方面：（1）碳纤维束脆性高，为避免夹持力过大导致夹碎碳纤维，在分离的碳纤维束两端保留一部分碳基体，使拉伸载荷直接作用于碳基体；（2）碳纤维束形变小，形变量不易准确测出，因此应保证标距段的长度；（3）碳纤维束拉伸强度高，而纤维束/基体界面剪切强度相对较低，为避免低应力状态下纤维束从基体中拔出，设计足够长的加载段；（4）从试验成本和试样加工程序考虑，试样不宜过长。最终选定试样长度为180mm，标距段28mm，两端加载段各为70mm，过渡段各6mm。加工试样的过程如图1所示。

2.2 实验结果

图1 碳纤维试件加工过程示意图Fig.1 Processing route of carbon-fiber sample

拉伸实验在ZWICK万能力学试验机上进行，剪切实验在岛津DSS-10T-S材料试验机上进行。实验结果列于表1，其中拉伸模量和剪切模量分别给出了XY向和Z向的结果。

表1 力学性能实验结果Table.1 Test results of mechanical properties

3 复合材料有效性能预报

3.1 宏观性能的预报方法

对于单向纤维增强复合材料，设其总体积为v，将纤维看成圆柱状均匀地排列在基体材料中，其体积为vf，那么基体组分的体积为（vm=v-vf）。根据Eshelby等效夹杂理论［7］可知，当设给定复合材料在其边界上受到远场均匀的应力σ0时，另外有一形状相同的均质材料，其弹性性质与上述复合材料的基体弹性性质相同，在同样的外力作用下，它在基体材料中的平均应力σm为：

式中L0是基体材料的弹性常数张量。由于夹杂相的存在，实际复合材料基体的平均应变不同于ε0，将由夹杂相间的相互作用产生一个扰动应变ε~。这样，复合材料基体中的平均应力为：

显然，基体中应力的扰动部分为：

由于材料弹性性质的差别，在外力场作用下，复合材料纤维夹杂相内的平均应力与平均应变又不同于基体内的相应平均值，它们的差值为σ′与ε′。这个在基体平均背应力σ0+σ~基础上的纤维夹杂的应力扰动问题可以用Eshelby等效夹杂原理来处理，

其中L1为纤维材料的弹性常数张量，ε*为纤维的等效本征应变。σ′与ε′为由于单个纤维的存在引起的扰动应力和应变，沿用Eshelby的推导结果有：

这里S为四阶Eshelby张量，它与基体的弹性性质及纤维的形状有关。将（5）式代入（4）式得

其中△L＝L1-L0；材料的体积平均应力应等于其远场作用的平均应力σ0，根据应力平衡条件，有：

利用（1）、（4）和（5）式的关系，由上式得：

将（6）式代入（9）式，可以解出：

其中k=（S-I）（△LS+L0）-1。同样得到等效本征应变与不存在夹杂时外载引起的基体应变之间关系：

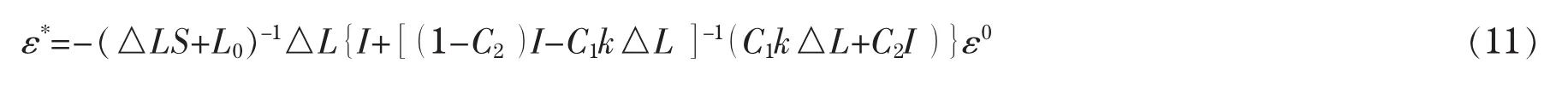
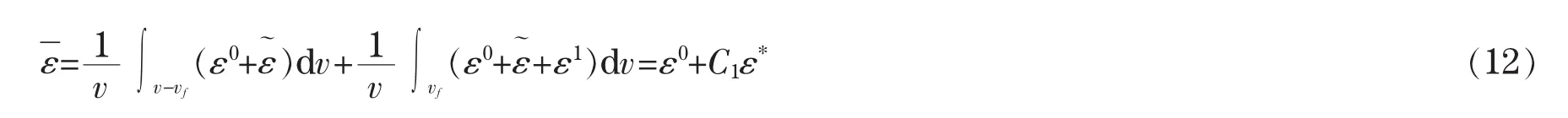
在均匀外应力场作用下求出平均应变场，可以得到复合材料的宏观弹性性能。

3.2 细编穿刺碳/碳复合材料的力学性能预报

碳/碳细编穿刺复合材料结构如图2所示，xy向织物为层叠碳纤维束（Nx=Ny=1K）编织八纹缎布（缎数Sxy=8），Z方向穿刺纤维由碳纤维束（Nz=8K）组成，碳纤维的直径均为df=7μm。预成形件经过化学气相沉积（CVD）处理，然后进行多次加压浸渍——碳化——石墨化循环过程，石墨化温度在2000℃以上，最终制成的复合材料件中，穿刺纤维束间平均距离为Tz=1.2mm，Z方向每厘米厚度内碳布为40-45层 （H=40/cm）。根据细编穿刺织物的微结构形式（如图2所示），X，Y，Z三个方向上纤维束的有效横截面积分别为：

图2 碳/碳编织复合材料成型及结构示意图Fig.2 Processing route and architecture of braided C/C composites

如果将Z方向纤维束视为一根圆截面纤维，xy向纤维束视为椭圆截面纤维，其中椭圆纤维的短轴半径a=10/（80*2），则相对纤维的等效半径为：

根据该结构的周期性排布规律，选取一代表性体胞单元，z方向取单位长度，其它两个方向尺寸分别为：

那么单胞在x，y，z三个方向上的纤维体积百分含量分别为：

单胞内部纤维的总体含量Vf=Vfx+Vfy+Vfz，将三维编织复合材料视为体平均意义下单向模型的等效迭加，利用刚度平均化方法可得到相应的细编穿刺复合材料整体刚度矩阵：

图3 不同取向纤维束的方位角Fig.3 Directional angel of fibre bundle with different orientation

其中：l1=cosΦ；l2=sinΦcosθ；l3=sinΦcosθ；m1=0；m2=sinθ；m3=-cosθ；n1=-sinΦ；n2=cosΦcosθ；n3=cosΦsinθ。根据刚度平均化方法，令：

式中vf是编织复合材料所有纤维织物的体积，vfn是第n类纤维所占的体积。上式kn代表单胞内不同方向纤维取向对整体刚阵的贡献系数。

4 数值计算结果与分析

将实验得到的碳纤维与石墨基体的拉伸模量代入式（17），求得细编穿刺C/C复合材料的弹性常数，具体结果如表2所示，表中以实验值为真实结果给出了预报误差。表2表明拉伸实验中的纵向拉伸模量预报值比实验值大，这主要由于z向穿刺纤维在工艺过程中造成纤维断裂等损伤和界面脱粘等缺陷的影响造成的；此外，剪切模量的预报误差比拉伸模量预报误差较大的原因与二者的实验条件不同有关。总体来讲，理论预报值与试验值之间的误差在10%以内，可以认为理论预报值较可靠，计算模型假设合理，计算结果可信。

5 结论

（1）根据组元材料特点，建立了拉伸试样的加工方法、利用拉伸和剪切实验获得了组元材料及复合材料的常温力学性能参数。

（2）以细观力学中的有效性能预报理论和方法为基础，用FORTURN语言编制了源程序，对细编穿刺碳基复合材料的常温下的弹性模量进行了理论预报，预报值与实验值的最大误差为9.5%，表明理论预报值较可靠，计算模型假设合理，计算结果可信。

（3）分析了误差产生的原因与工艺过程及实验条件有关。

［1］Torsten W，Gordon B.Carbon-carbon composites：a summary of recent developments and applications［J］.Materials&Design，1997，18（1）：11-15.

［2］Pindera.An Experimental Investigation of Iosipescu Specimen for Composite Materials［J］.Comp.Mater.1987，21（12）：1164-1184.

［3］Blucher JT， Dobranszky J， Narusawa U， Aluminium double composite structures reinforced with composite wires

［J］.Materials Science and Engineering.2004，A 387~389：867-872.

［4］Lissart N，Lamaon J.Statistical analysis of failure of SiC fibres in the presence of bimodal flaw populations［J］.Journal of Materials Science.1997，32：6107-6117.

［5］杨彩云.碳纤维、碳纤维织物及碳布在复合材料中强度的利用率的研究［J］.纤维复合材料，1998，3：46-50.

［6］方岱宁，周储伟. 有限元计算细观力学对复合材料力学行为的数值分析［J］.力学进展，1998，28（2）：173-188.

［7］Hashin Z.Theory of Mechanical Behavior of Heterogeneous Media［J］.Appl.Mech.Rev.1964，17：1-9.

［8］Hill R.Continuum Micro-Mechanics of Elastic Polycrystals［J］.J.Mech.Phys.Solds.1965，13：89-101.

Research on Micromechanical of Effective Properties of Carbon-based Composite

ZHOU Zhen-yun，HU Yao-hua，MA Li
(School of Physics&Electronics Engineering,Taizhou University,Taizhou 318000,China)

As a kind of heterogeneous material,the mechanical properties and failure rule of carbon-based composites has close relationship with the elastic constant and volume constant of component as well as microconfiguration.Based on the respective characteristics of components carbon fiber,graphite and carbon cloth,a tensile property test method was established,and then failure strength,elastic modulus and tearing strain under normal temperature were obtained in this work.Based on the test results,Eshelby equivalent inclusion theory and Mori-Tanaka method were used to establish the corresponding models to predict the elastic constant of carbon based composites under normal temperature. Results show that theoretical prediction is in good agreement with the test data,which proves that the method is valid.

carbon based composite;components;tensile test;micromechanical

周小莉）

TB332

A

1672-3708（2011）03-0014-06

2010-10-22；

2010-11-05

浙江省自然科学基金资助（资助号Y4100185）

马 李（1974- ），男，黑龙江哈尔滨人，博士，讲师，主要从事新型结构材料制备研究。