论类型逻辑语法对蒙太古语法的继承与发展

王欣

当代逻辑语法(logical grammar)出现于1970年代，是国外语言学研究的一支主流，在国内尚处于起步阶段。逻辑语法是语言学、数学和逻辑学的交叉学科，探求自然语言的数理结构，对自然语言信息处理具有直接的应用价值。

蒙太古语法(Montague Grammar，简称MG)由美国逻辑学家蒙太古(R.Montague)创立。他把语言学看作数学的分支，是一种应用数学。①方立:《逻辑语义学》，北京:北京语言大学出版社，2000年，第1页。MG最有影响的成果是有关英语量化和内涵语义现象的部分语句系统(fragment)，②Montague，R.，“The proper treatment of quantification in ordinary English”，in J.Hintikka，J.Moravesik，and P.Suppes(eds.)Approaches to Natural Lnauge，Dordrecht:Reidel，1973，pp.221-242.一般称为PTQ系统。1990年代，逻辑语法进入类型逻辑语法(Type－Logical Grammar，简称TLG)发展阶段，Carpenter写出了标志性的专著。③Carpenter，B.，Type-Logical Semantics，Cambridge:the MIT press，1997.本文在前人基础上着重从语言学的角度论述类型逻辑语法如何发展了蒙太古语法。④参见邹崇理:《逻辑、语言和信息——逻辑语法研究》，北京:人民出版社，2002年;邹崇理:《范畴类型逻辑》，北京:中国社会科学出版社，2008年;张秋成:《类型逻辑语法研究》，北京:中国人民大学出版社。比较二者异同，有助于了解、推动该学科的发展。

一、逻辑语法的基本思想

转换生成语法使句法可计算的认识深入人心，但语义如何计算?在那些同时配备了句法学和语义学的数理逻辑系统里，语义是生成性的、可计算的，于是蒙太古试图建立一种通用语法(universal grammar)，使之能够统一生成和解释人工语言和自然语言。蒙太古语法最大的贡献在于，第一次证明自然语言的语义也可以像句法那样进行精确、系统的表达和计算。

组合性原则是逻辑语法的根本原则:一个表达式的意义是其组成部分的意义及其组合方式的函数。该原则表达了三层意思:第一，自然语言的语义可计算;第二，意义计算既涉及单位意义，又涉及单位意义的组合方式;第三，复杂意义是上述计算的结果。

逻辑语法由句法学和语义学两部分构成，前者生成合法的语符串，后者生成语义。句法部分用范畴语法(categorial grammar，简称CG)表述，CG是一种生成语法，由一个递归定义的句法范畴集合和数量极少的几条规则构成，依生成能力大小有多种变体。语义部分用高阶内涵逻辑(intensional higher-order logic，简称IL)表达，逻辑系统作为一种(人工)语言有自己的句法学和语义学，IL的句法学由句法范畴(俗称“语义类”(semantic type))集合和几条句法规则组成，可生成合规则的复杂逻辑表达式。IL的语义学包含一个抽象的数学模型和一套语义计算规则，可计算出逻辑表达式的语义值。

逻辑语法的语义学富有特色，它是派生性的(derivational)，跟构型性的(configurational)乔氏生成语法的语义理论不同。①Bach，E.，Informal Lectures on Formal Semantics，SUNY series in linguistics，Albany，N.Y.:State University of New York Press，1989，p.48.简单地说就是跟句法生成一样，语义是一步步计算出来的，而不是先生成一个句子，再给它一个一次成型的语义解释。逻辑语法计算语义时，先把自然语言翻译为逻辑语言再对后者做语义计算，这种方法称为间接的语义解释。

本文关于蒙太古语法的讨论以PTQ系统为例。PTQ系统有一个翻译部分，其功能一是把基本的自然语言表达式翻译为IL表达式，二是为每一自然语言句法规则制订一条相应的翻译规则，也称语义规则，以便每进行一步句法运算，都能同步翻译为IL表达式，这种模式称为“规则对规则假说”(rule-to-rule hypothesis)。IL的语义类指派函数为每一CG的句法范畴指派一个且仅指派一个IL语义类。语义类指派函数和规则对规则模式保证了句法计算和语义计算的同步性和系统性。类型逻辑语法跟蒙太古语法的内部构造和运行方式大致相同，也采用间接的语义解释，但是没有PTQ那样的翻译部分，范畴运算规则跟语义类运算规则直接对应。

PTQ用黑体书写自然语言表达式，用白体书写逻辑语言表达式，比如walk的逻辑表达式是walk’。类型逻辑语法用白斜体书写自然语言表达式，用黑正体书写逻辑表达式，比如walk的逻辑表达式是walk。PTQ有两个原子句法范畴:e和t，TLG有三个:np、n和s。PTQ的高阶内涵逻辑有两个原子语义类:e和t，②跟原子句法范畴写法相同，好处是直接体现了句法和语义的对应，坏处是容易引起混淆。类型逻辑语法也有两个原子语义类:Ind和Bool。

二、蒙太古语法和类型逻辑语法的联系与区别

类型逻辑语法(TLG)由蒙太古语法(MG)发展而来，二者最重要的区别在于类型逻辑语法更严格地贯彻了组合性原则。

1.同现范畴符号与组合性原则

蒙太古语法PTQ系统共有17条句法/翻译规则，其中一部分没有严格贯彻组合性原则，比如有关并列结构的规则11把某些表达式作为“同现范畴符号”(syncategorimatic element)直接插入语法运算。根据第一节提到的规则对规则假说，PTQ每一条规则都分成句法和翻译两部分:

S11:若α，βϵPt，则F8(α，β)，F9(α，β)βϵPt，其中F8(α，β)=αandβ，F9(α，β)=αorβ。

T11:若α，βϵPt，并且α，β分别译为α’，β’，则αandβ译作α’＜β’，αorβ译作α’＜β’。

S11说的是:给定任意两个t范畴的表达式α和β，经过F8或F9的操作，得到另一t范畴表达式αandβ或αorβ。T11说的是:给定任意两个t范畴的表达式和的翻译式α’和β’，αandβ译为α’＜β’，or译为α’＜β’。

PTQ的CG里，句法规则和句法操作分离，前者规定输入什么范畴的表达式可以输出什么范畴的表达式，后者规定如何把输入的表达式连缀成一体。最常用的句法操作是毗连，比如给定John和love，毗连得到John love或love John。给定两个t范畴表达式，比如John walks和Mary talks，F8和F9的操作结果分别是John walks and Mary talks和John walks or Mary talks。这里and和or不像其他表达式那样有自己的句法范畴，也没有独立的逻辑翻译式。另外，规则11两个输入表达式的范畴相同，都是t，彼此无法做泛函运算。从句法上看，and和or像是从天而降，跟另外两个表达式一下子连接在一起;从语义上看，形如and的表达式直接译为α’＜β’。像and、or这样通过为其量身定制的规则进入句法/语义运算的成分被称为同现范畴符号。

类型逻辑语法不存在同现范畴符号。它定义了逻辑常项and和or，其语义类是Bool→Bool→Bool。联结两个小句的and就被翻译为逻辑常项and，其句法范畴是ss/s，表示先毗连右侧一个s范畴表达式，即小句，再毗连左侧一个s范畴表达式，得到一个更大的句子。这样就更严格地贯彻了组合性原则，使逻辑表达式及其推演更接近自然语言的样子。

PTQ用规则12和13处理谓语并列结构(比如walks and talks)和名词短语并列结构(比如John or Mary)，TLG如何处理这些现象?回答是通过“多形态并列组合器”(polymorphic coordination combinator) Coorσ。所谓“组合器”是一种没有常项和自由变项的λ-词项(比如λxλP.P(x))，它所代表的语义对象没有非逻辑常项那样的描写性语义内容，也不具备逻辑常项可以决定一个逻辑推导是否有效的逻辑学意义。Coorσ的语义类是(Bool→Bool→Bool)σ→σ→σ，σ是个变项，代表任意布尔类，表达为σϵBoolType。所谓布尔类就是最终输出类是Bool的语义类，比如Bool，Ind→Bool，(Ind→Bool)((Ind→Bool)(Ind→Bool))。最简单的布尔类即Bool，相应最简单的并列组合器就是CoorBool，其语义类是(Bool→Bool→Bool)Bool→Bool→Bool，要求输入一个语义类为Bool→Bool→Bool的逻辑表达式，比如逻辑常项and，得到另一个相同语义类的表达式CoorBool(and)，即联结小句的and的逻辑表达式。如果and联结的是两个语义类为Ind→Bool的谓语，则先把组合器CoorInd→Bool应用于and，得到类型为(Ind→Bool)((Ind→Bool)(Ind→Bool))的语义表达式CoorInd→Bool(and)，再先后与talks和walks组合，即可生成并解释walks and talks。Coorσ(and)常简写为and:

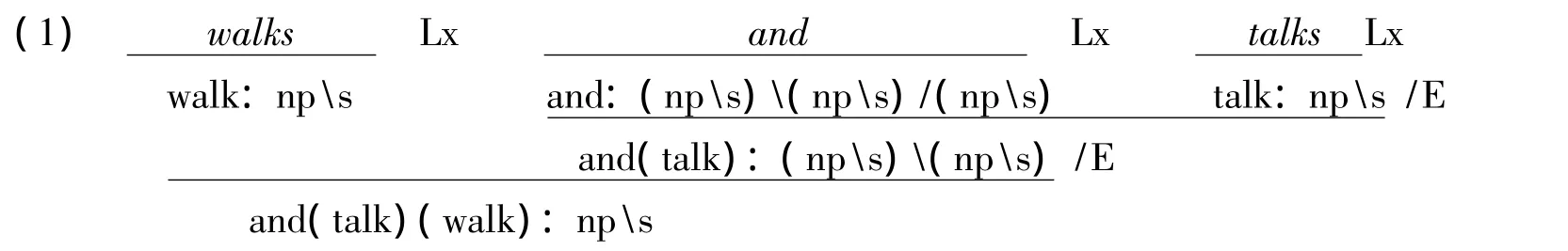
/E表示顺向斜线消去的句法运算，E表示逆向斜线消去，其意义请见下节。John and Mary可得到类似处理。相应地，and在词库里记录如下:and⇒Coorσ(and):AA/A，Typ(A)=σϵBoolType。这个词条严格说来是一组，因为A是个范畴变项，表示任意语义类为布尔类的句法范畴。这意味着and在词库里的词条可以是无穷多:and可以联结多少不同范畴的表达式，词库里就会有多少and“词条，反映了范畴语法是所谓“最激进的词汇主义语法”。①Carpenter，B.，Type-Logical Semantics，p.437.这样类型逻辑语法不仅可以处理PTQ里的三种并列结构，还可以处理自然语言可能出现的各种并列结构。类型逻辑语法更严格地贯彻组合性原则的另一原因跟它所采用的CG有关。

2.蒙太古语法PTQ和类型逻辑语法的范畴语法

PTQ的CG不是“纯粹的”范畴语法。②Dowty，D.，Word Meaning and Montague Grammar，Dordrecht:Reidel，1979，p.11.首先，PTQ句法规则的表达形式不同于纯粹的范畴语法，后者句法规则数目极少，都是规则范式，比如下面(a)是顺向泛函运算规则(forward functional application，简称FA)，(b)是该范式的两个特例:

而PTQ的句法规则都是特例性质的，不是规则范式。第二，PTQ句法规则和句法操作分离，同一句法规则可涉及不同的句法操作(比如规则11)，同一句法操作也可用于不同的句法规则，纯粹的CG则没有这个特征。自然语言形态变化丰富，PTQ需要大量的句法操作以保证生成形态正确的英语句，比如对动词进行时态、人称、数和否定操作的F4以及F11至F15。

PTQ的CG其生成能力总体上相当于古典CG，而TLG采用的CG则达到了兰贝克演算(Lambek calculus)的生成能力。古典CG的双向泛函运算规则在兰贝克演算里表述为双向斜线消去规则，此外增加了双向斜线引入规则:

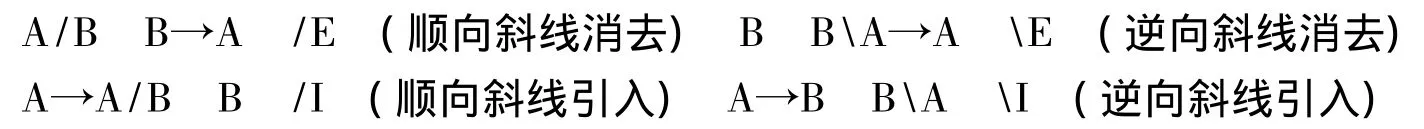
兰贝克演算是一公理化的、纯粹的CG，其句法规则都是规则范式，不区分句法规则和句法操作。

3.词库和自然语言向逻辑语言的翻译问题

PTQ的词库非常简单，由所有基本表达式集合的并集构成，只记录词形和句法范畴，比如IV范畴(t/e范畴的简写式)基本表达式集合是BIV={run，walk，talk，rise，change}。基本表达式在翻译部分经翻译函数的运算译为IL逻辑表达式。TLG的词库则非常丰富，不仅词条数量增加了，词条记录的信息也增加了，每一词条可形式化的表达为e⇒α:A，e表示词形，α表示逻辑翻译式，A表示句法范畴。词语的形态句法变化都记录在词库里，比如:

类型逻辑语法不需要PTQ那样的翻译部分，因为第一，词库直接记录了基本表达式的逻辑翻译式，并通过如下词汇插入范式进入句法和语义计算:

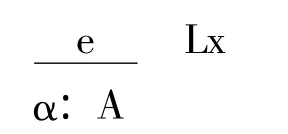
第二，词库记录了词语的形态句法变化，无需制定专门的句法操作。第三，PTQ里的同现范畴符号在类型逻辑语法里都被指派了句法范畴并获得独立的逻辑翻译式，其身份不再特殊，也就不必为其制定专门的句法和翻译规则。从微观角度看，蒙太古语法和类型逻辑语法的异同在名词短语和量词辖域等问题上显现突出，下面以名词短语的逻辑语法处理为例具体说明。

三、关于名词短语的逻辑语法处理

英语NP有多种句法形式，包括专有名词、代词以及语义上包含“全部、某个、大多数、很多”等数量意义的量化NP，比如every man、some woman、most parks、a lot of pens。它们的句法分布相同，PTQ第一次统一处理了各种NP的句法和语义生成，其方法是把T范畴(复杂范畴t/(t/e)的简写式)统一赋与各类NP，其中专名和代词构成词库里的集合BT，规则2把同现范畴符号a、the、every放在普通名词之前得到T范畴的量化NP。T范畴表达式的语义值是广义量词(generalized quantifier)，即论域个体集合之集合。把T范畴统一赋予各种NP还可以很容易地生成John or every kid这类结构。

Partee认为这样做有两个问题:一是在传统一阶谓词逻辑里，专有名词和代词语义上指谓模型论域里的个体，比如John指某个名叫约翰的个体，这比广义量词的解释(即所有叫约翰的那个人所在的个体集合的集合)更符合直觉。第二是语义计算过程极为复杂。①Partee，B.，“Noun phrase interpretation and type－shifting principles”，in P.Portner and B.Partee(eds.)Formal Semantics:the Essential Readings，Blackwell，2002，pp.357-381.Dowty认为心理现实性不是蒙太古语法谋求的目标，语义计算的复杂性对计算机来说也不是问题。②Dowty，D.，“Compositionality as an empirical problem”，p.65.还有学者试图改进NP的处理，类型逻辑语法提供了一个方案。

类型逻辑语法把范畴np直接赋予专名和代词，其语义类为Ind，指谓论域个体，使得专名和代词的语义解释更符合直觉，减少了计算的复杂性。量化NP的句法范畴是np⇑s，范畴运算符称为“设域器”(scoping constructor)，定义为:

如果A，BϵCat，则B⇑AϵCat。Typ(B⇑A)=(Typ(B)→Typ(A))→Typ(A)

np⇑s范畴的语义类是(Ind→Bool)→Bool，指谓广义量词。同斜线算子一样，⇑也可以被引入和消去，在生成图上分别记为⇑I和⇑E。引入设域器可以很容易地处理John or every kid一类表达式:范畴为np的John经过引入运算变为np⇑s范畴的表达式，这样就和every kid范畴相同了，应用并列组合器Coornp⇑s(and)即可生成John or every kid。同and和or一样，every、a和the等限定词在类型逻辑语法里也不再是同现范畴符号，它们被指派了范畴np⇑s/n。以every为例，类型逻辑语法定义了逻辑常项every，其范畴是np⇑s，语义类是(Ind→Bool)→Bool，它是everyone、everybody、everything等词语的翻译式，限定词every可以在此基础上定义为every2=defλP.λQ.every(λx.P(x)Q(x))。every kid的生成过程是:

类型逻辑语法和蒙太古语法一脉相承，内部构造和运行机制大致相同，但类型逻辑语法改进了范畴语法和高阶内涵逻辑这两个理论构件，因而对自然语言句法和语义的计算更简便，也更好地实现了组合性原则。通过本文的简要分析，希望能引起读者作深入的兴趣，并结合汉语检验和发展这些理论。