基于内模原理的汽车主动悬挂系统的减振控制*
2011-01-10窦同水唐功友
窦同水,唐功友
(1.山东化工职业学院,山东淄博255400;2.中国海洋大学信息科学与工程学院,山东青岛266100)
汽车悬挂系统的质量对于提高汽车的性能,如汽车的行驶乘适性、操纵稳定性等,具有重要的作用。因而,汽车悬挂系统的减振控制问题成为一个热门的研究课题。现代汽车主要有3种类型的悬挂方式,即被动悬挂,半主动悬挂,和主动悬挂[1,2]。相对于被动悬挂和半主动悬挂而言,主动悬挂可以改善悬挂系统在大频率范围内的减振性能,并且能适应基于持续扰动力的系统变化[1]。从1960年代以来,现代汽车主动悬挂系统得到了迅猛发展,主动悬挂的减振控制研究受到广泛关注。例如利用预测控制[3],模糊控制[4],H∞控制[5]和预见控制[6]等手段研究主动减振控制问题取得了许多好的研究成果。由于路面粗糙度以及路面对汽车行驶的扰动力是随机的,所以将控制理论直接应用于受随机路面扰动的主动悬挂系统受到了限制。
本文试图将路面粗糙度对汽车主动悬挂系统的持续扰动模型近似用未知振幅和初相位的Fourier级数有限和表示,并在此基础上研究汽车主动悬挂系统基于内模原理的减振控制问题。
1 问题描述
1.1 系统描述
考虑如图1所示的单自由度四分之一汽车主动悬挂系统。
对现代化轿车来说,汽车悬挂的减振作用主要取决于悬挂弹簧和减振器的特性,轮胎对减振的作用与悬挂弹簧和减振器相比要小得多。为了更准确地研究悬挂弹簧和减振器对汽车减振的影响,在本文中假设轮胎是一个刚体,因此车架位移zu(t)等于路面激励输入zr(t),即zu(t)=zr(t)。
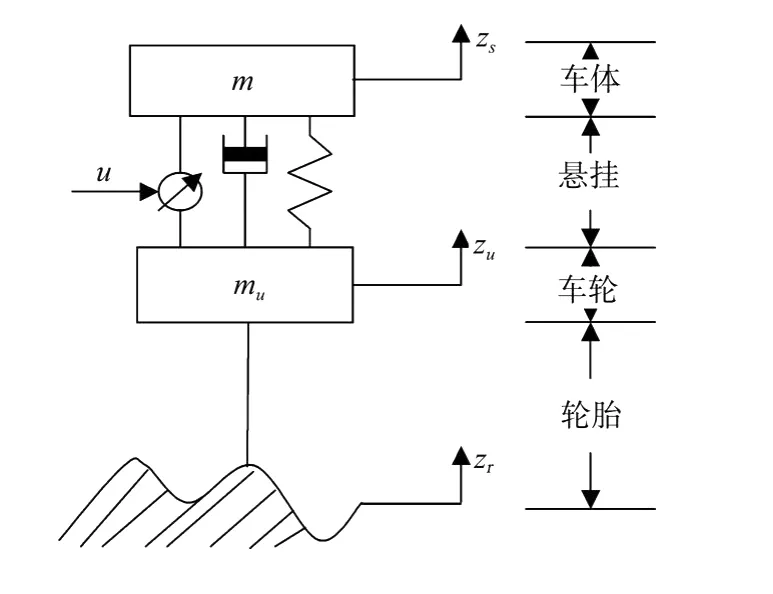
图1 四分之一汽车主动悬挂模型Fig.1 Quarter active suspension model of the car
至此汽车主动悬挂系统的动力学模型可以简化为如下的二阶受扰系统:
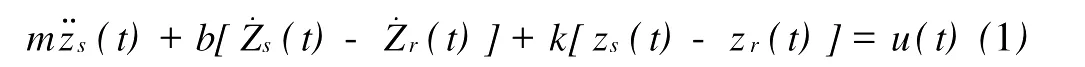
其中m为车体簧载质量,k和b分别是未受约束时悬挂的刚度和阻尼系数,zs(t)是车体垂直位移,zr(t)是路面激励输入,u(t)为施加于悬挂系统的控制力,可以由液压或其它减振器产生。
选择状态向量
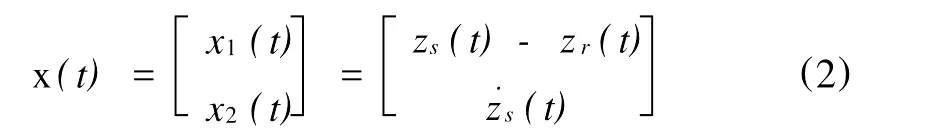
其中,x1(t)为车身与车架之间的相对位移,也称为悬挂动挠度,x2(t)为车体簧载质量的垂直速度。至此,主动悬挂系统(1)就转换为如下状态空间形式
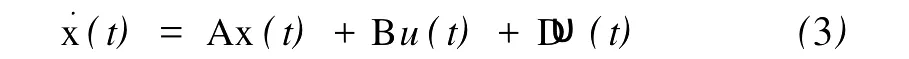
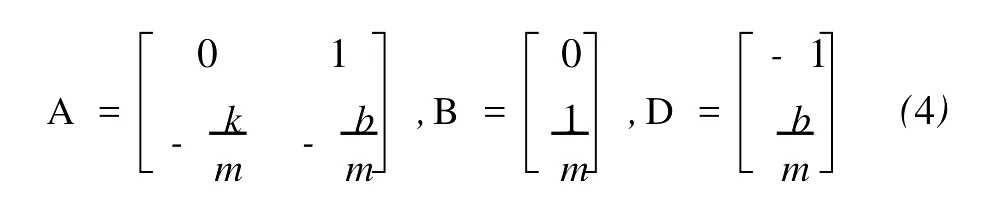
1.2 扰动分析
为了提高汽车在乘适性、易操作性等几方面的性能,需要考虑路况问题[5]。通常汽车悬挂系统的振动起因于路面的不平度。在工程实际中,路面的不平度可用给定路面位移功率谱密度(PSD)的随机过程进行拟合[7]。
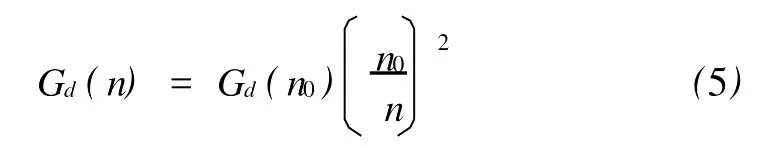
其中,n表示空间频率,它是波长的倒数,表示每米长度中包含的波数,量纲为:m-1,n0=0.1 m-1为参考空间频率。中国国家标准GB7031-86给出了路面粗糙度分级的Gd(n0)建议取值,其量纲为10-6m3。
在本文的研究中,将路面的不平度视为汽车悬挂减振控制系统的主要扰动。由(3)和(4)可知,汽车悬挂系统的固有频率为汽车悬挂系统在固有频率附近的扰动较敏感。为了简化问题,根据减振性能的要求,只考虑汽车悬挂系统在固有频率附近的扰动,即设定汽车悬挂系统的固有频率范围为[ω1,ω2]有效空间频率n∈[n1,n2]=[ω1/υ0,ω2/υ0],其中υ0为汽车的行驶速度。
假设路面扰动zr(t)近似为时间的周期函数。由于悬挂系统本身具有低通滤波的特性,可以只考虑频率较低的路面位移扰动。因此,路面随机位移扰动可以用以下Fourier级数的有限和近似表示[8]:
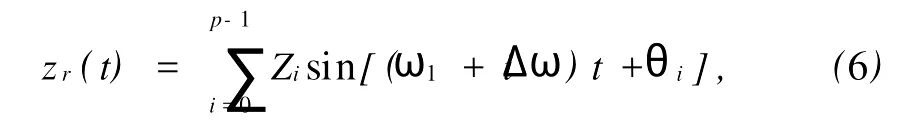
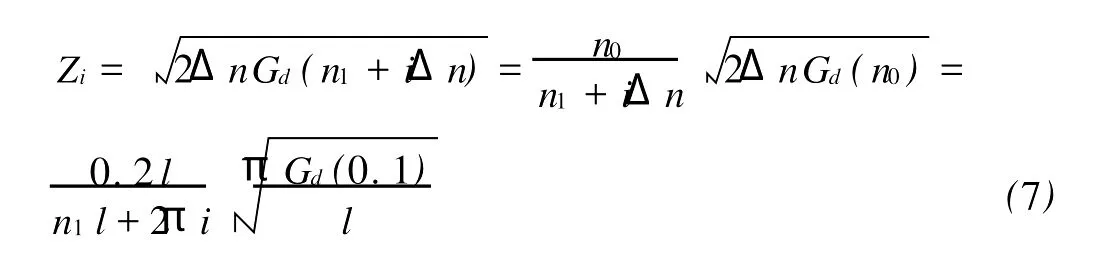
这里,Δω=2πυ0/l,Δn=2π/l,l为路段的长度。由此可以得到路面随机速度扰动的有限和近似表达式:
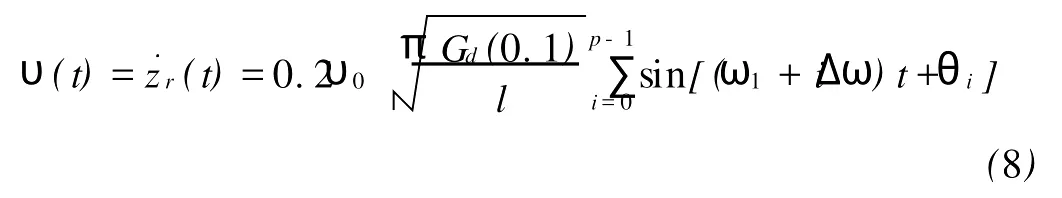
为了设计减振控制器的方便,需要将路面扰动用状态空间表达式近似描述。定义扰动状态向量

系统(3)的路面扰动输入υ(t)可用如下外系统描述

其中G∈R2p×2p,F∈R1×2p为常量矩阵,且有

显然,描述路面扰动的外系统(10)与路面随机速度扰动(8)是等价的。
2 减振控制律的设计
根据系统(2)和扰动外系统(10),设计基于内模原理的减振控制律

其中K1为维数匹配矩阵,通常它由单位阵或零矩阵构成;K2和K3为待定的控制增益矩阵。闭环控制系统的结构如图2所示。

图2 闭环控制系统的结构图Fig.2 Block diagram of the closed-loop control system
将控制律(12)代入系统(3)可以得到汽车悬挂控制的闭环系统

闭环系统的极点为矩阵
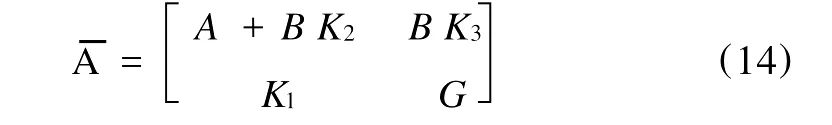
的特征值。
下面讨论K1,K2和K3的设计问题。由于汽车悬挂和轮胎本身的频率特性都具有低通滤波特性,所以扰动(8)的高频分量可以由汽车悬挂和轮胎本身有效地抑制。在设计减振控制律(12)时,可以只考虑扰动(8)的低频部分。为了研究的方便,取p=1,即
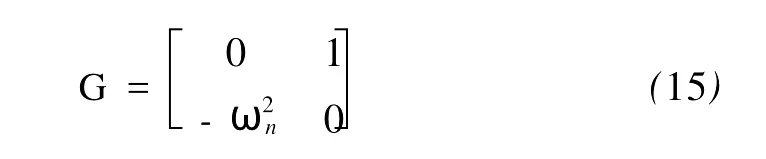
选取(15)后,闭环系统(13)是1个4阶系统。假设要求闭环系统的极点为s1,s2,s3和s4。其闭环系统(13)的特征方程具有以下形式
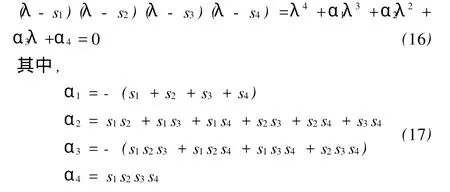
而K1是2×2矩阵,在此选择K1=I。K2和K3是1×2矩阵,所以2个矩阵共包含4个要设计的矩阵元素,而由(16)和(17)知,恰好有4个方程可以利用。由假设及(14),可以得到闭环系统(13)的特征方程为
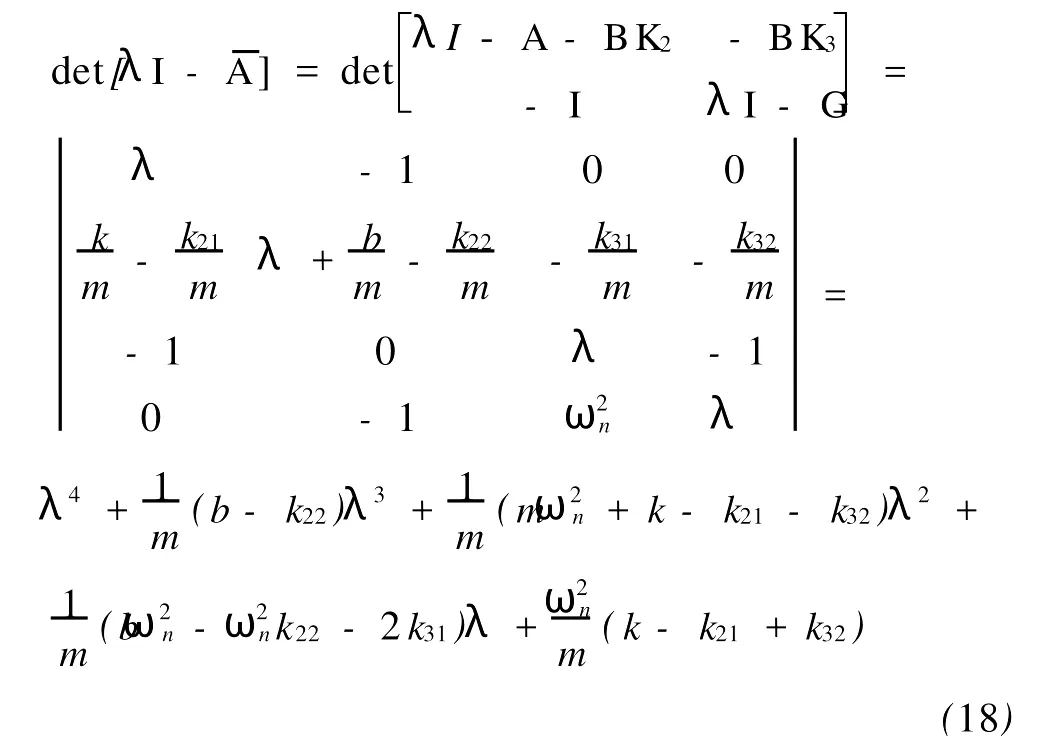
比较(16)和(18)的系数,得到

从而得到减振控制律为
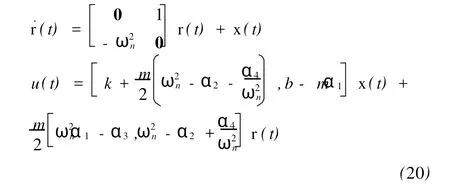
3 仿真示例
将所设计的控制律应用到四分之一汽车主动悬挂模型上进行仿真实验。汽车悬挂系统的参数如下[9]:车体簧载质量m=504.5 kg,悬挂刚度k=13 100 N/m,悬挂阻尼系数b=400 Ns/m。控制力u(t)的量纲为N,这样,主动悬挂系统(3)中的矩阵取值为
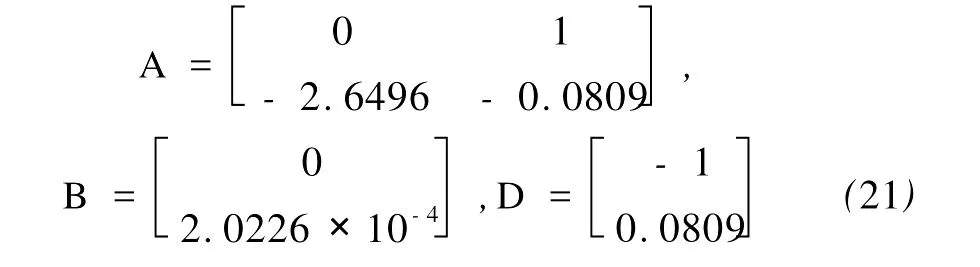
在此例中,选取υ0=20 m/s,l=200 m。选择路面为B级粗糙度,根据国家标准GB7031-86,路面的PSD的平均值为为了使模拟路面的动态位移扰动更接近实际路面,在模拟路面的动态位移扰动时选择β1=0.5,β2=5,从而得[ω1,ω2]=[0.6511,8.1388]。图3显示了路面的动态位移扰动。
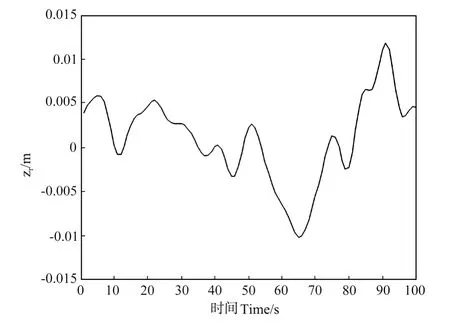
图3 路面位移扰动Fig.3 Road surface displacement disturbance
在设计减振控制律时,取p=1。并要求闭环系统(13)的极点为s1,2=-1±0.5 j,s3,4=-3±j。由(19)和(20)可以得到减振控制律

从图4、图5和表1可以看出,在本文所设计的减振控制律的作用下,主动悬挂控制系统在车体垂直振动加速度¨zs(t)和垂直振动速度(t)=x2(t)的响应振动幅度明显比开环系统小,即在所设计的控制器作用下,车辆的乘适性有明显的提高。
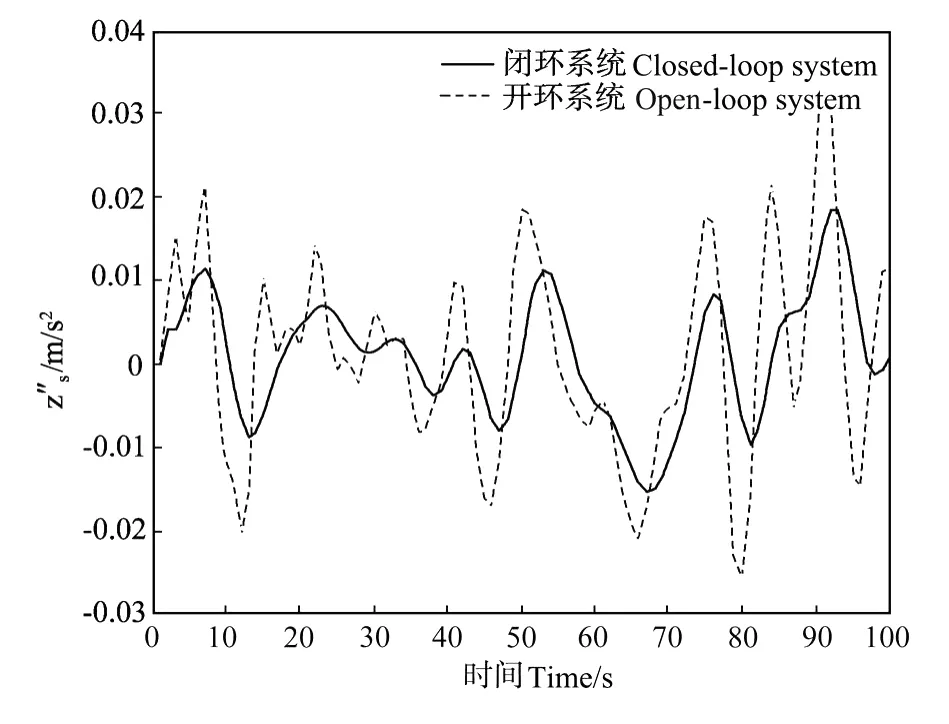
图4 车体垂直加速度的响应曲线Fig.4 Vertical acceleration response curves of the car body
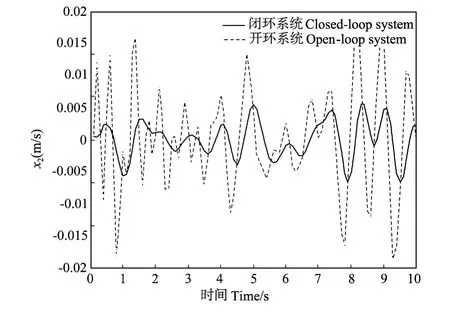
图5 车体垂直速度的响应曲线Fig.5 Vertical velocity response curves of the car body
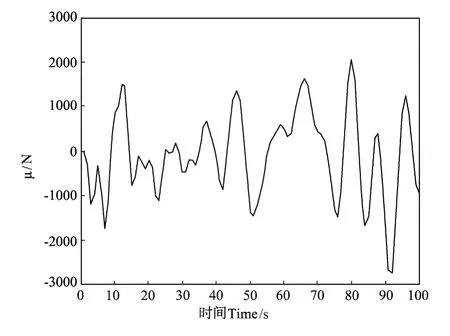
图6 控制输入曲线Fig.6 Curve of the control input
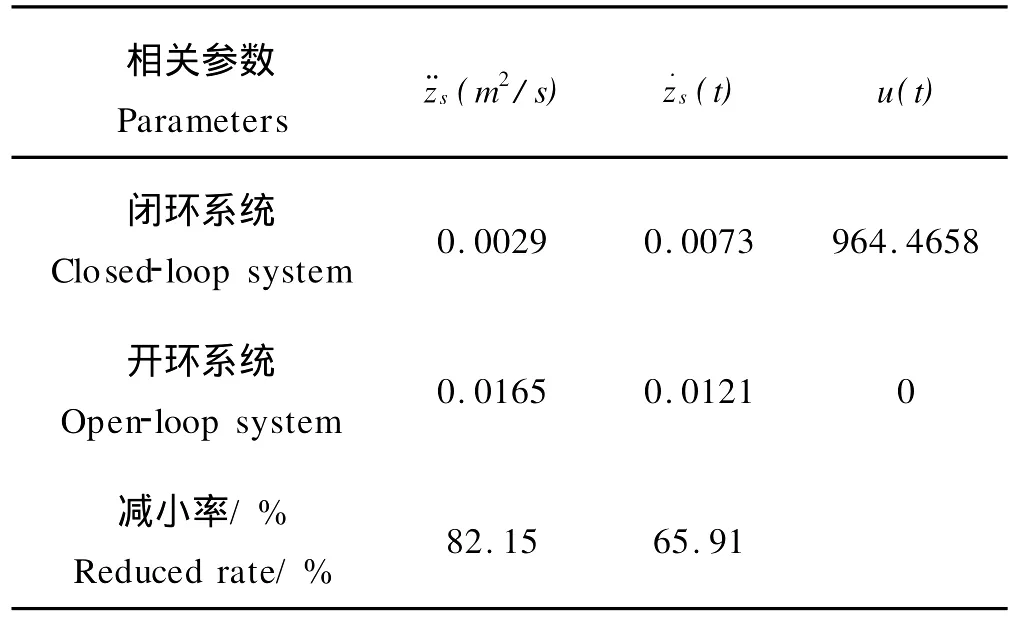
表1 系统响应和性能指标的均方根值Table 1 System response and performance of the mean square root value
4 结语
本文建立了单自由度四分之一主动悬挂系统和路面粗糙度扰动模型,设计了汽车主动悬挂系统基于内模原理的减振控制律。仿真结果表明,设计的控制律简单易行,减振控制效果较满意。
[1] Hrovat D.Survey of advanced suspension developments and related optimal control applications[J].Automatica,1997,33(10):1781-1817.
[2] Gao H,Lam J,Wang C.Multi-objective control of vehicle active suspension systems via load-dependent controllers[J].Journal of Sound and Vibration,2006,290:654-675.
[3] Chisci L,Rossiter J A,Zappa G.Systemswith persistent disturbances:Predictive controlwith restricted constraints[J].Automatica,2001,37:1019-1028.
[4] A l-holou N,Lahdhiri T,Joo D S,et al.Sliding mode neural network inference fuzzy logic control for active suspension systems[J].IEEE Transactions on Fuzzy Systems,2002,10(2):234-246.
[5] Du H,Zhang N.H∞control of active vehicle suspensions with actuator time delay[J].Journalof Sound and Vibration,2007,301:236-252.
[6] Mianzo L,Peng H.LQ and H∞preview control for a durability simulator[C].American Automation Control Council.Proc of A-merican Control Conference.Albuquerque,New Mexico:IEEE Press,1997:699-703.
[7] GBPT703121986,车辆振动输入与路面平度表示方法[S].北京:中国标准出版社,1987
[8] 郑军,钟志华.非线性汽车行驶平顺性模型的神经网络优化[J].汽车工程,2001,23(3):172-176.
[9] Jalili N,EsmaiL,Zadeh E.Optimum active vehicle suspensions with actuator time delay[J].Journal of Dynamic System s,Measurement,and Control,2001,123:1447-1455.
