基于根轨迹法的海洋生态模型稳定性分析*
2011-01-10刘珑龙曲伟玉王美健
刘珑龙,曲伟玉,王美健
(中国海洋大学数学科学学院,山东青岛266100)
由于海洋的特殊物理性质,海洋生态系统较陆地生态系统要复杂得多,其稳定性也远比陆地要低[1]。进入1990年代,关于海洋生态系统的研究异常活跃,并开始研究系统的“动力学”特征。目前,国内外学者在海洋生态动力学模型的建立和处理方法上做了很多研究[2-5]。
本文就一类NPZ非线性海洋生态模型,应用Lienard-Chipard条件判定其稳定性。并通过控制理论中的广义根轨迹法分析得出,参数取值不同时对系统稳定性能的影响。该方法刻画了随着参数的增大,特征方程的根在复平面的分布,因此可捕捉到系统的稳定性能变化,但是其精度取决于高阶项。
1 模型的引入
浮游动物对浮游植物的摄食过程采用Lo tka-Volterra公式,本文采用营养盐(N)-浮游植物(P)-浮游动物(Z)模型[6],建立海洋生态系统方程如下:

模型参数的意义及取值如表1所示[7]。

表1 生态动力学模型参数含义及取值Table 1 Parameters and values of ecological dynamic model
设Nf=+x4,其中,表示t=0时平衡状态,营养盐的输入,不妨设x4为单位阶跃函数x4=,γ,Rm,α,rN,εZ,εP互不相关,且各个参数均大于0,那么:

其中u=(N P Z)′
当t<0时,令f(u)=0,可求得方程(1)的非平凡平衡点:

2 模型的稳定性分析
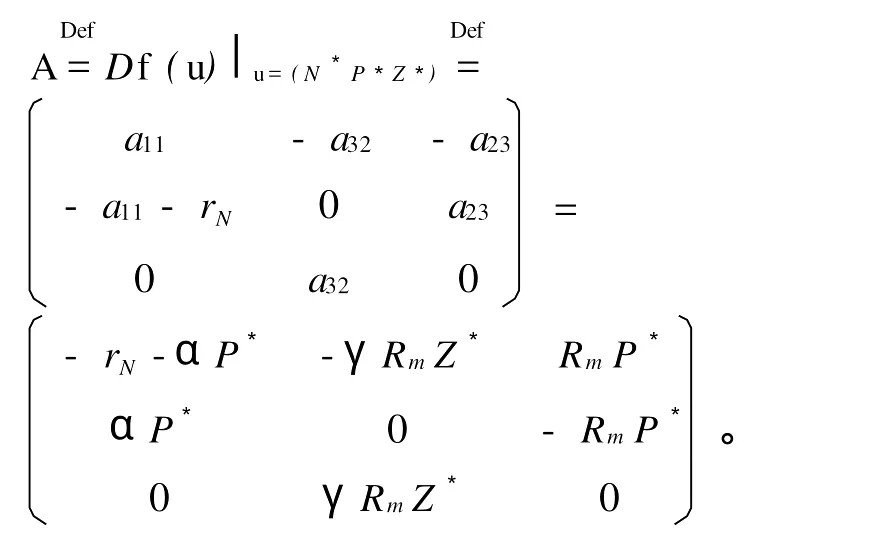
经验证,只需Z*,rN,γ,α,Rm均不为0,则A不存在实部为零的特征根,该条件满足方程(1)的假设,其在平衡点(N*P*Z*)是双曲的。
以下研究方程(1)在平衡点(N*P*Z*)的局部稳定性。
根据稳定性定理可知,若A的特征根的实部均小于0,则方程(1)是稳定的[8],但三阶特征多项式根的求解较复杂,因此,本文采用Hurw itz判据的等价判据Lienard-Chipard判据[9],来判断特征根实部的符号。
|λI-A|=λ3-a11λ2-a32(a23+a11+rN)λ-a23a32rN=0具有负实部的特征根的充分必要条件是:
1)λ的各项系数大于0,由a11,a23,a32的定义可知:
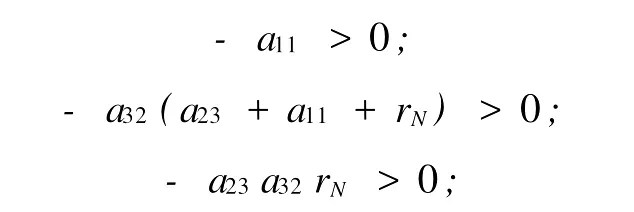
2)偶数阶的Hurw itz行列式大于0,由|λI-A|和a11,a23,a32的定义可知:
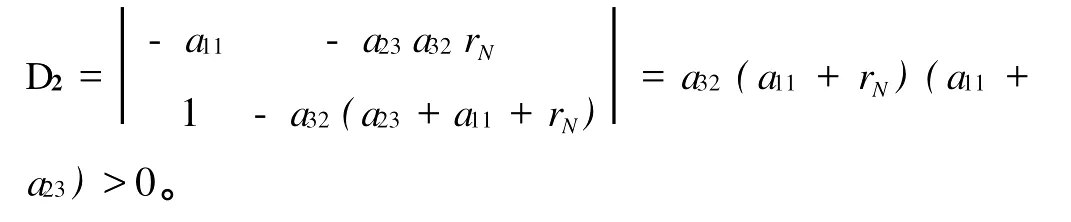
3 广义根轨迹法对系统稳定性进行的分析
3.1 传递函数
下面考虑方程(1)的等价系统,不妨设x1=NN*;x2=P-P*;x3=Z-Z*;x4=Nf-;可以把方程(1)等价转化为以下系统:

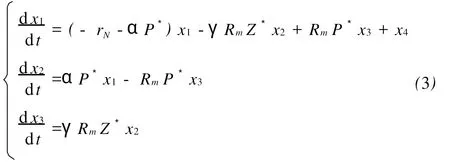

由于该方程的初值x=(000)′,对方程(3′)进行Laplace变换,在复频域上讨论其稳定性能。
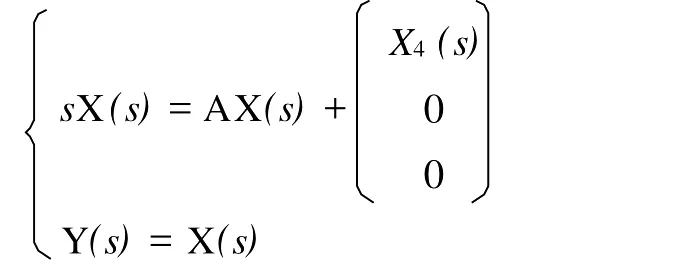
其中X(s),X4(s),Y(s)是x,x4,y的Laplace变换,则:

可求得传递函数:

3.2 广义根轨迹法
系统的稳定性和相关性能指标主要是由闭环系统的极点在复平面的位置决定的,为了求出闭环极点需要求解高阶代数方程,三阶以上的代数方程求解是较困难的。每当有参数变化时,需要重新求解高阶代数方程[11]。广义根轨迹法,是针对系统中的某一参数从0变化到+∞时,确定系统极点在复平面的变化曲线。本文采取广义根轨迹的方法,可以不用求解代数方程,就能确定出某个参数变化时极点的位置变化。把各参数带,可得:

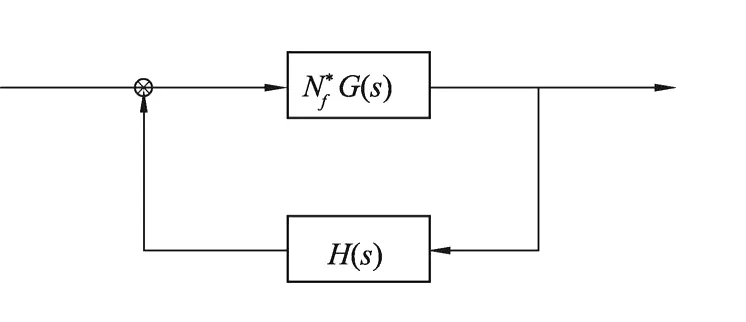
图1 增益的等效控制图Fig.1 Equivalent control figure of gain
其中,D(s)=s3+1.3s2-0.084s-0.0012;N(s)=21s+0.3;可画出的根轨迹图,如图2所示:

图2 增益的根轨迹图Fig.2 Root locus figure of gain
2)由根轨迹法得知,当极点之间的距离加大时,系统的动态过程会尽快的消失。由图2可知,当时,<(s)的极点之间的距离增大,则方程(3)的动态过程会尽快的消失。对于方程(2)取时间长度为1 000,时,其相轨迹图和时间历程图见图3~6。
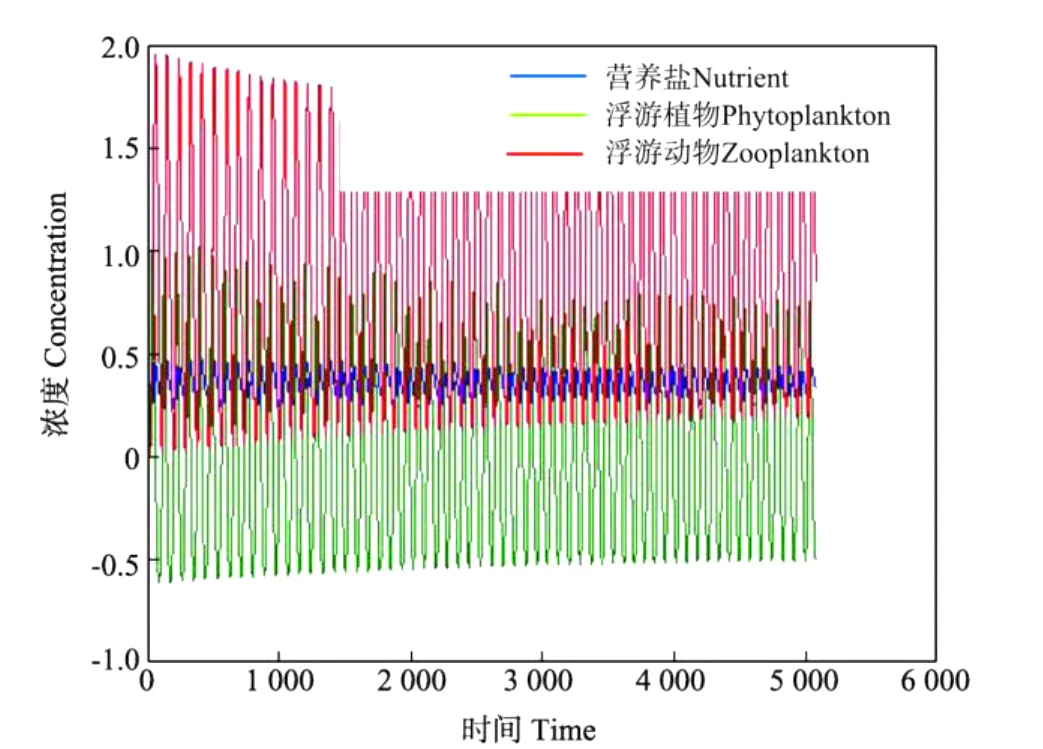
图3 =0.024的时间历程图Fig.3 The time course figure w hen=0.024

图4 =0.024的相轨迹图Fig.4 The space trajectory figure when=0.024

图5 =0.025的时间历程图Fig.5 The time course figure w hen=0.025

图6 =0.025的相轨迹图Fig.6 The space trajectory figure when=0.025
4 结语
判断海洋生态系统在平衡点的稳定性时,通常随着变量的增多,代数方程的求解难度加大,从而造成平衡点稳定性分析的难度增加。本文采取Hurw itz判据,可在不求解代数方程零点的情况下,即可判断出系统的稳定性。
经过分析可知,当浮游植物的生长率α和初始时刻营养盐的输入均大于浮游植物的死亡率εP和营养盐的流失率rN时,系统存在稳定状态。若浮游植物的生长率和初始时刻营养盐的输入增大时,或浮游植物的死亡率和营养盐的流失率减少时(即初始时刻的浮游动物Z*浓度增大),系统的动态性能减小,即系统会更快的趋于稳定状态。可见,浮游动物的含量在整个海洋生态系统中,起着至关重要的作用。
[1] 苏纪兰,唐启升.我国海洋生态系统基础研究的发展——国际趋势和国内需求[J].地球科学进展,2005,20(2):139-143.
[2] 王洪礼,葛根.变参数赤潮藻类生长模型的非线性动力分析研究[J].海洋通报,2007,26(3):48-52.
[3] Zhao Qiang,Lu Xianqing.Parameter estimation in a three-dimensional marine ecosystem model using the adjoint technique[J].Journal of Marine System s,2008,74:443-452.
[4] Gianpiero Cossarini,Cosimo Solido ro.Global sensitivity analysis of a trophodynamic model of the Gulf of Trieste[J].Ecological modeling,2008,212:16-27.
[5] 冯剑丰,李会民,王洪礼.浮游生态系统非线性动力学研究[J].海洋技术,2007,26(3):67-69.
[6] 陈长胜.海洋生态系统动力学与模型[M].北京:高等教育出版社,2003:179-284.
[7] 赵淑江.胶州湾生态系统主要生态因子的长期变化[D].北京:中国科学院研究生院,2002.
[8] Hirsch M W,Smale S.微分方程、动力系统和线性代数(下册)[M].北京:高等教育出版社,1987:1-14.
[9] 张琪昌,王洪礼,竺致文,等.分岔与混沌理论及其应用[M].天津:天津大学出版社,2005:1-35.
[10] 廖晓昕.稳定性的理论、方法和应用[M].武汉:华中科技大学出版社,2002:153-216
[11] 程鹏.自动控制原理[M].北京:高等教育出版社,2003:63-111.
