植物河道河相关系动态调整*

陈 举,拾 兵,刘 勇

(中国海洋大学工程学院,山东青岛266100)

河道中的植物群落对于复式河道内的水流特性产生重要影响,即植物因子对河相关系动态调整的作用是十分显著的。近年来,随着生态河流建设步伐的不断推进,人们加深了对植物河道水沙特性的理解。但其河相关系的研究,仍是植物河道设计控制理论与堤岸生态修复技术中的热点与难点问题。

目前对植物河道河相关系的研究甚少。仙农熵的引入,可作为分析水力学及河流动力学中一些随机特性变量变化规律的有效工具[1-3]。Cao(1995,1996)、Cao&Knight(1999)对冲积河流的稳定床面形态作了研究[3-4]。拾兵、王燕等[5](2010)利用仙农熵理论推导了沙质河床无植物作用时的河相关系动态调整关系,并通过物理模型试验进行了验证,得到了令人满意的计算表达式。本文拟对植物河道河宽动态调整进行非线性分析和试验研究,旨在建立植物作用下的河相关系动态调整表达式。

1 理论推导

1.1 仙农熵

对于1个事件X,其信息量l(X)可用该事件出现概率p(X)的负对数来表示,即

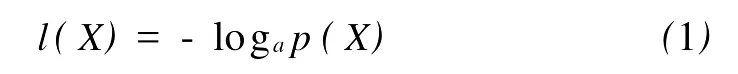
对于某个物理量的仙农熵的定义为其平均信息量。连续变量y的仙农熵H(y)为其数学期望,用概率密度函数可表示为:

式中:p(y)为概率密度,p(y)d y则为该物理量在y至y+d y区间内出现的概率。

1.2 公式推导

与推导无植物河道河相关系动态调整公式类似[5],为得出考虑植物因子在内的河相关系系数的动态调整公式,需采用最大熵原理。从物理意义上看,ζ的最大熵导致在满足约束的前提下,ζ的概率分布趋于均匀。决定ζ的概率分布和大小取决于边界条件。

图1 植物河道河相关系系数时间变化示意图Fig.1 A schematic draw ing of hydraulic geometry facto r varying with time

从理论上讲,ζ在(0,T1)内是递增的,之后便趋于稳定。对于T1以后的时间,ζ1出现的概率为1,其仙农熵为0(见图1)。下面探讨(0,T1)内的情况。

当T=0时,ζ=ζ0;当T=T1时,ζ=ζ1。在时间段(0,T1)内,均可进行河相系数的采样计算,即各时间点具有相同的采样概率。考虑河相系数随时间递增的关系,河相系数小于或等于ζ的概率是T/T1。河相系数对应的累积概率分布函数为:

则其概率密度函数为:

式(4)所示函数应满足概率空间的性质,即随机概率空间全概率定义和数学期望定义这2个约束条件:

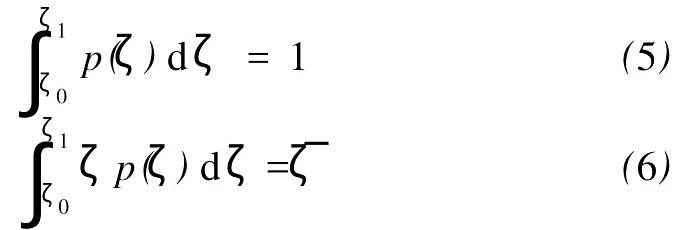
由式(2)知,河相关系系数在ζ0和ζ1之间的概率熵为:

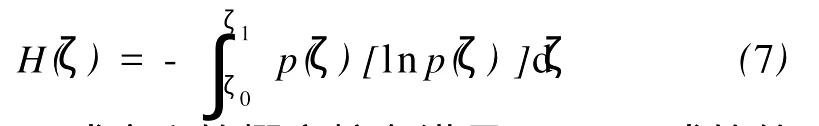
为求解(7)式定义的概率熵在满足(5)、(6)式的约束条件下的极大值,采用变分法求解,约束条件为等式的条件极值。即满足方程:

式中:λ1,λ2为拉格朗日算子。求解式(8)得河相系数概率密度函数为

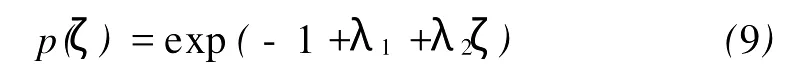
将式(9)代入约束条件(5)式和(6)式,则求出拉格朗日算子λ1和λ2为:

将式子(9),(10)和(11)代入式(7)可得熵

由式(4)和式(9)知,各式右边相等,即

解(13)式可得河相系数动态变化的表达式:

式(15)描述了由概率熵导出的植物河道河相系数动态变化表达式,当a=0时,即可化成无植物河道的情况。

2 参数k的敏感性分析

借助物理模型试验,对k值进行敏感性分析。本试验为概化的复式植物河道物理模型试验,满足重力相似准则,几何比尺λL=20。试验河道为顺直型,模型控制流量80～140 m3/h,每种工况试验时间为3 h。即当试验接近3 h左右,河床变形很小,可视为河道宽度调整基本稳定。

植物布置见图2。滩地种植麦冬草,采用规则布置,排列方式为10 cm×10 cm。由于根系的不规则性,采用根系的面积比率来计算根系影响,即a=0.018。试验测算所得河相系数各时间点的值见表1。式(15)各参数取值见表2。

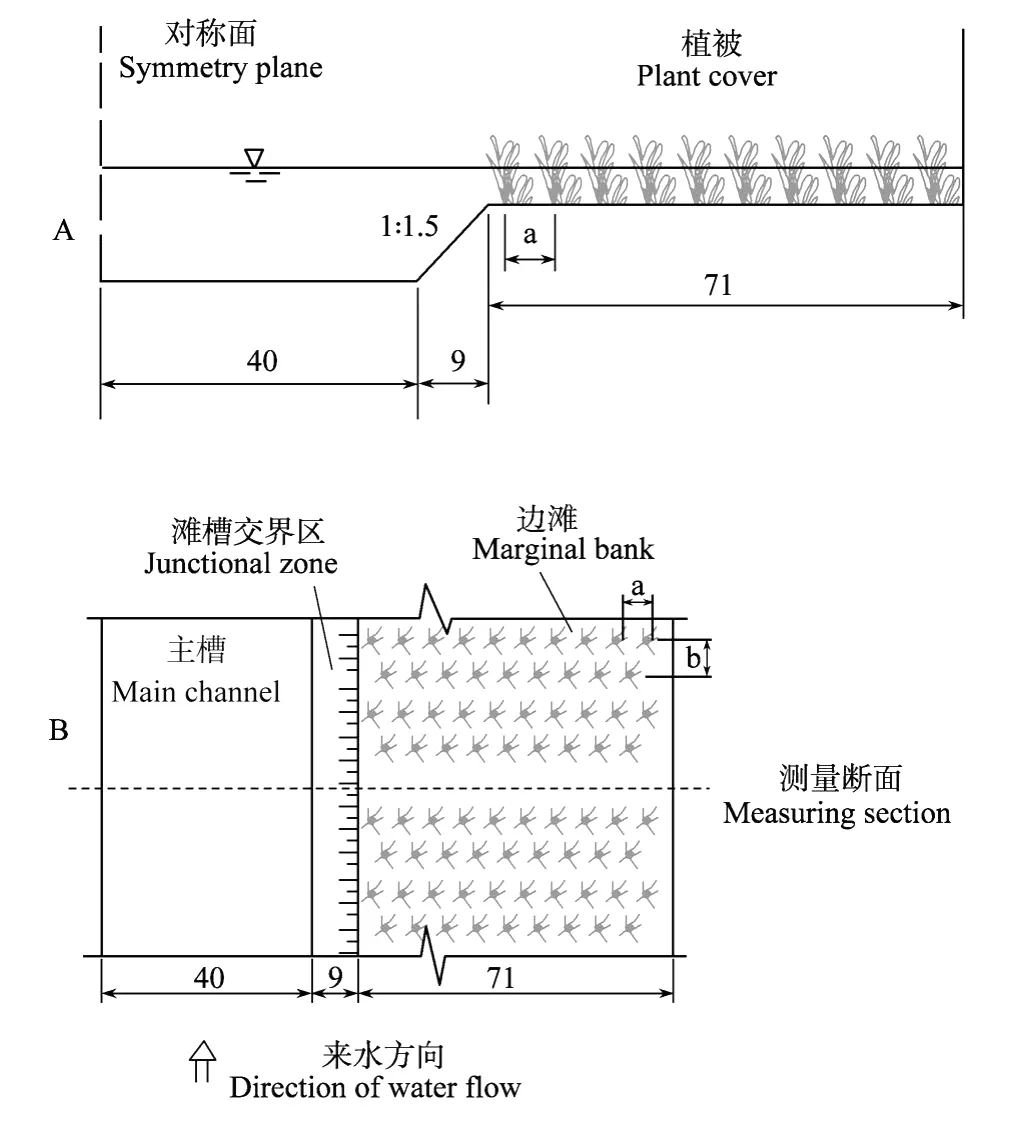
图2 植物河道宽度调整试验布置剖面图(A)和平面图(B)Fig.2 Profile chart(A)and plan view(B)for testing rrangement of width adjustment in a vegetated channel model

表1 河相系数实测值Table 1 Measured values of hydraulic geometry factor

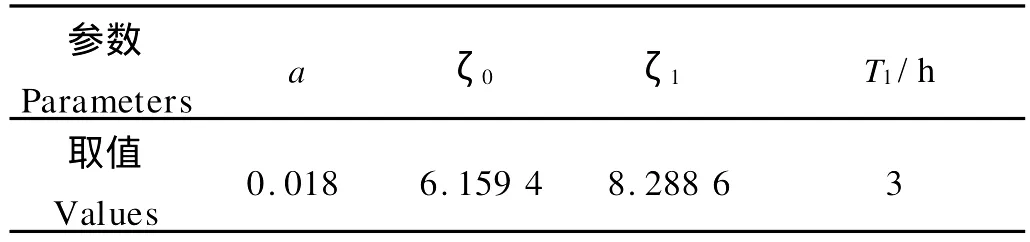
表2 相关参数取值Table 2 Values of related parameters

图3选取了几个不同的k值,绘出了相应的河相系数动态曲线。当k<0时,式(15)对k的敏感性很差。当控制k在20～30,其效果良好,误差较小。通过误差分析,k取25时误差最小。图4为计算值与实测值的比较,可以看出计算值与实测值非常接近。

由此可知,k的取值决定了式(15)的精确性。只要知道了初始和稳定2个状态的边界条件,即可推求区间内的任意时刻的河相关系系数。

图3 k的敏感性分析Fig.3 Sensitivity analysis of k

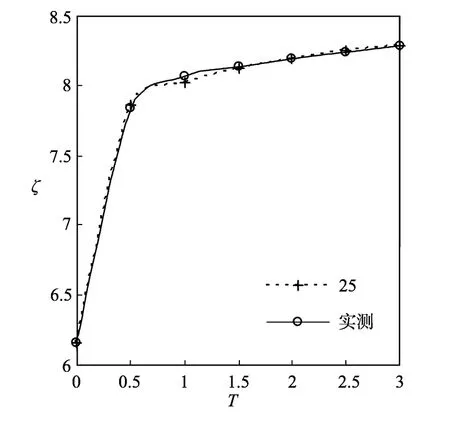
图4 河相系数计算值与实测值的比较Fig.4 Comparison values of hydraulic geometry factor in calculating and measuring

3 对植物因子a的分析

在图2所示的植物河道中,又进行了4种植物排列方式的试验,流量控制在80 m3/h左右。试验中测取了稳定后的河宽、水深,并计算对应河相系数,其相关数据见表3。

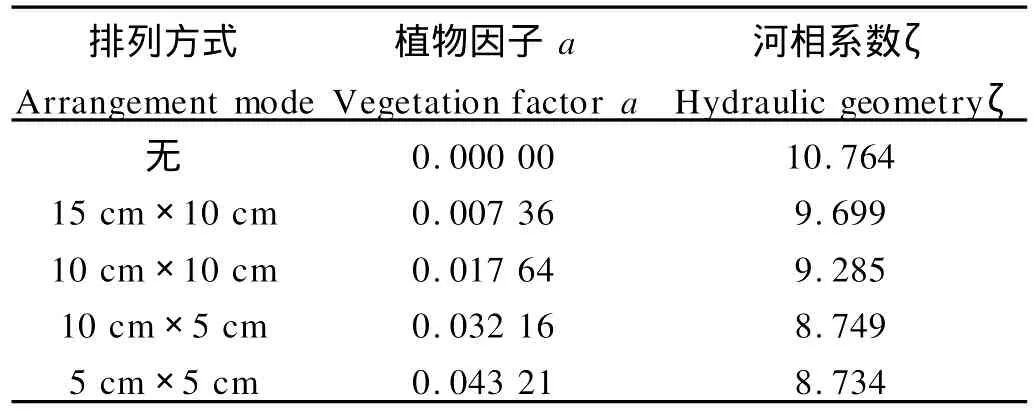
表3 植物因子与河相系数关系Table 3 Relationship between vegetation factor and hydraulic geometry

拟合表3中的数据,可得植物因子与河相关系之间的关系曲线,(见图5)。其拟合方程为:

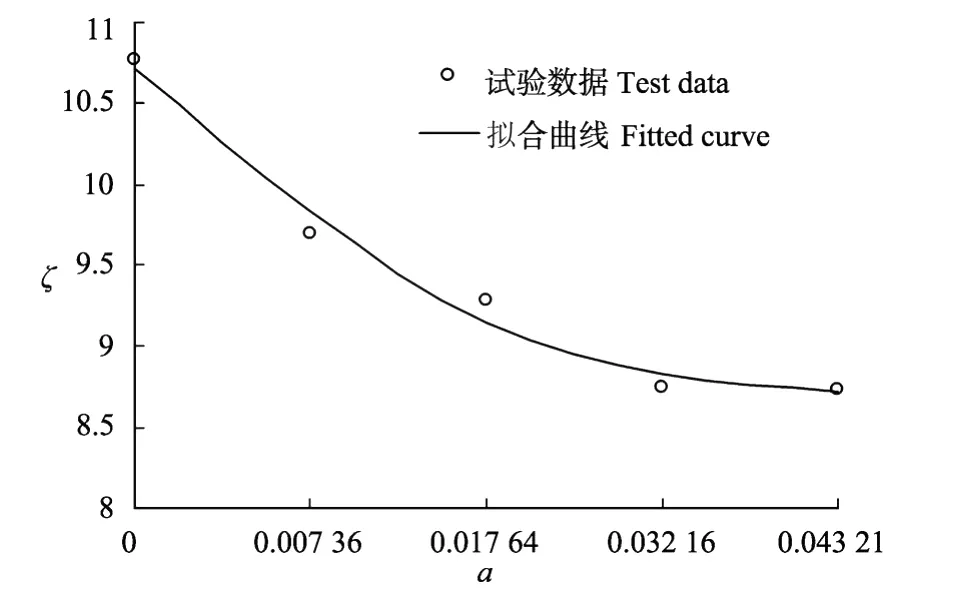
图5 稳定河相关系拟合曲线Fig.5 Fitted curve of stable hydraulic geometry with test data

由上图可以看出,河相系数随着植物因子的增加而递减。说明植物河道河相关系系数受植物影响明显。当滩地种植植物后,因植物根系的作用,河宽调整受到限制,河道向窄深型发展。

4 结论

(1)本文提出了植物河道的河相系数动态变化表达式(15),并将植物影响因子考虑其中,若无植物,即可还原至无植物河道的河相系数动态变化式。

(2)计算时的初始和稳定状态的河相系数,是控制该表达式的2个边界条件。有了这2种状态参数,任意时刻的河相系数随植物因子呈现非线性变化规律。

(3)植物影响因子只考虑了根系的作用,因其影响的复杂性,若考虑枝叶作用的影响,尚需进一步研究。

[1] Chiu Chao-lin.Entropy and p robability concep ts in hydraulics[J].J Hyar Engr,1987,113(5):583-600.

[2] Cao Shuyou,Chang H.Entropy as a probability concep t in energy-gradient distribution[C].∥Proc Nat Hydr Engr Colorado Sp rings CO,USA:ASCE,New York,1988:1013-1018.

[2] Cao,Shuyou,Regime theory and a geometric model for stable alluvial channels[D].U K:The University of Birmingham,1995:80-350.

[3] Cao Shuyou,Chang H.Entorpy as a p robability concept in energygradient distribution[C].∥Proc.Nat,Hydr Engr,Co or ado Sp rings,CO,USA:ASCE,1988:1013-1018.

[4] Cao Shuyou,Knight D W.Entropy-based design approach of threshold alluvial channels[J].Journal of Hydraulic Research,IAHR,1997,35(4):505-524.

[5] 拾兵,王燕等.基于仙农熵理论的河相关系[J].中国海洋大学学报:自然科学版.2010,40(1):095-098.