水声信号时频分析方法比较及应用研究＊

姚玉玲，王 宁，石洪华，谭君红

（中国海洋大学信息科学与工程学院，山东青岛266100）

水声信号时频分析方法比较及应用研究＊

姚玉玲，王 宁，石洪华，谭君红

（中国海洋大学信息科学与工程学院，山东青岛266100）

浅海中的宽带水声信号传播呈现出频散的特点，通过高分辨率的时频分析方法可以刻画频散曲线。通过数值仿真和实验数据处理，对比分析几类常用的时频分析方法在提取宽带声信号频散曲线方面的性能。结果表明：STFT时频局部化精度不够高；在较强频散的情况下，DSTFT时频分辨率较高。WVD时频聚集性最好，但是有严重的交叉项干扰；固定核函数的CWD较好地抑制交叉项，时频分辨率虽优于STFT，但弱化了时频聚集性；AOK时频分布采用自适应高斯核函数，在抑制交叉项的同时，时频聚集性较好，有望较好地用于提取信号频散曲线。

WVD；自适应最优核；DSTFT

波导中声简正波的传播速度依赖于频率，其相速度、群速度随频率的不同而改变，这就称之为频散现象。浅海波导中的宽带水声信号传播呈现出频散的特点，导致信号波形、到达方位展宽、信噪比下降等。是制约浅海声源定位和水声通讯等研究的主要因素之一。此外，频散特性可以用于浅海环境声学参数反演研究［1－4］。如何提取不同号简正波的频散曲线是解决上述问题的关键。准确地提取频散特性主要取决于2个方面：第1，频散本身的物理特性；第2，数值计算时各种时频分析方法的时频分辨精度。本文的讨论主要集中在第2个方面。

信号的时频分析描述信号在不同时间和不同频率处的能量密度和强度。自Gabor提出时频分析思想以来，国内外学者研究了许多时频分析的新方法［5］，并将其应用于地震、生物医学等许多领域。在水声信号处理中，时频分析结果可用于水声目标定位、参数反演等方面。本文通过数值仿真和实验数据处理，对比分析了几类常用的时频分析方法：短时Fourier变换（STFT：Short Time Fourier Transform）、Wigner－Ville分布、Cohen类时频分布（CWD）、自适应最优核时频分布（AOK）以及频散自适应短时傅里叶变换（DSTFT）［6］在提取宽带声信号频散曲线的性能。讨论了各种方法的时频局部化精度、交叉项抑制、属性提取效果等.本文讨论的结果在水声信号处理时选用各种时频分析方法具有借鉴指导意义。

1 各时频分析方法的基本原理

1.1 短时傅立叶变换

短时傅立叶变换（STFT）是时频分析中最简单的

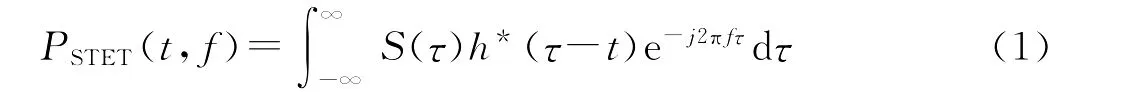
其中h（t）是窗函数，当窗函数确定后，相应的时间分辨率和频率分辨率也就确定了，是单一分辨率分析。

1.2 频散短时傅立叶变换［6］

STFT、CWT是线性变换，并没有考虑到信号频散的非线性特征，频散短时傅立叶变换考虑到频散的物理意义，旋转了变换的时频轴，当频散明显时，可提高时频分辨率。形式，是1种固定时间窗的时频分析方法，其基本思想是：用窗函数来截取信号，假定信号在窗内是平稳的，采用傅立叶变换来分析窗内信号，确定该时间存在的频率，然后沿着信号时间移动窗函数，得到信号频率随时间的变化关系：

1.3 Wigner－Ville分布（WVD）

Wigner－Ville分布（WVD）是1种最基本的双线性时频表示，WVD定义为

式（3）中不含有任何的窗函数，因此避免了短时傅立叶变换时间分辨率、频率分辨率相互牵制的矛盾，时频聚集性好，比线性时频表现出更高的分辨力。业已普遍承认，没有任何1种时频联合分布的时频分辨率能出其右，皆因其时间－带宽积达到了Heisenberg不确定性原理给出的下界。

虽然WVD对单分量信号具有很好的时频聚集性，但对于多分量信号，会产生交叉项问题。然而，浅海声传播是典型的多分量场，来自不同号简正波的贡献。

1.4 Cohen类双线性时频分布（以CWD为例）

为抑制WVD产生的交叉项，人们又提出了许多新型的时频分布。其中的双线性时频分布，如Cohen类双线性时频分布、自适应最优核时频分布等，均以WVD为基础，实质都是在设法保持WVD良好的时频聚集性的同时，尽可能地抑制或消除交叉项。Cohen定义信号s（t）的时频分布的统一表示形式为：

所有的Cohen类和自适应最优核时频分布都是基于信号的模糊域特征来抑制交叉项的，即利用了信号的自项通常聚集在模糊平面的原点附近，而交叉项远离原点的特性，核函数具有二维低通滤波器的性质

Choi－Williams提出的C－WVD方法其核函数为一指数核，即g（θ，τ）＝e－θ2τ2／σ。

1.5 自适应最优核时频分布（AOK）

自适应最优核时频分布的核是与信号相关的，具有一定的自适应性。

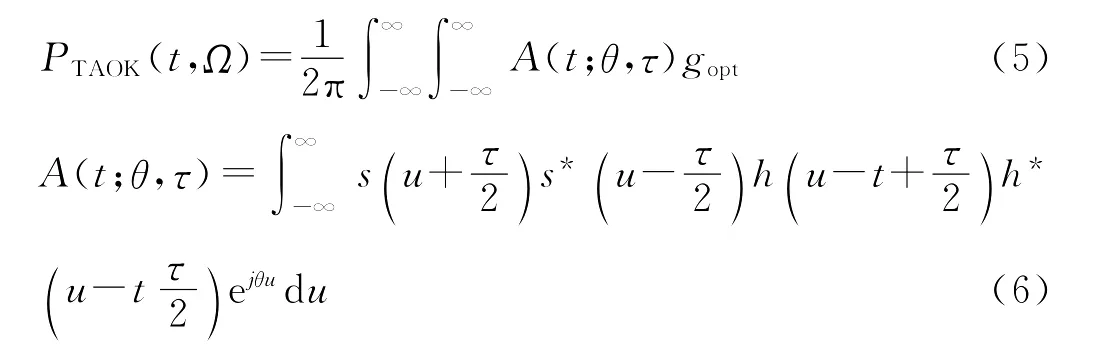
式中，A（t，θ，τ）为短时模糊函数，h（u）为对称窗函数，窗函数沿着时间轴滑动，对于信号的任何细节部分，短时模糊函数都可以准确的刻画出来。求解最优短时核函数g（t，θ，τ）可以通过求解下列最优化问题得到：其中，A（t；θ，τ）、g（t；θ，τ）为短时模糊函数和短时核函数在极坐标中的表示形式。

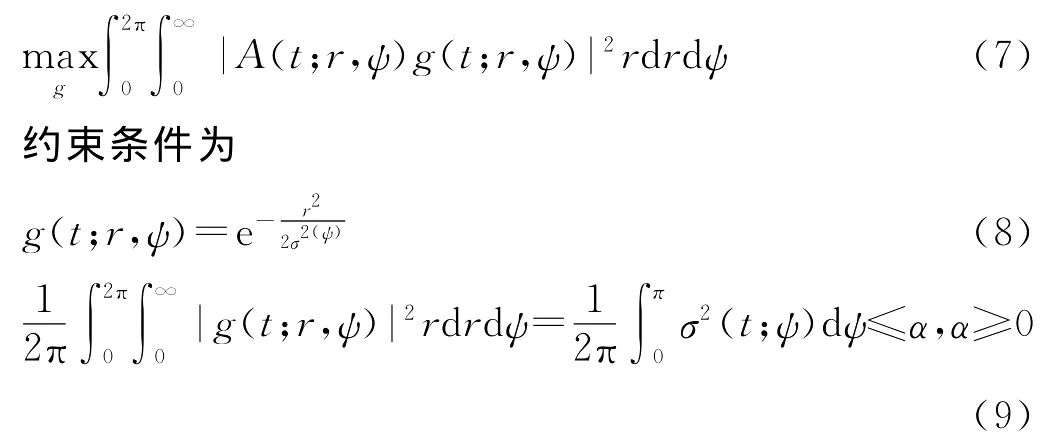
2 时频分析方法的比较与应用

为了对比各种时频分析方法的应用效果，分别对一水声仿真信号和2009年青岛崂山湾实验数据进行了时频分析。图1为仿真海洋环境参数、声速剖面分布、水声仿真信号及其STFT，DSTFT，CWD，WVD，AOK时频分析结果。

图1中水声仿真信号由Krakenc声场计算模型产生，其频带范围为200～500 Hz，信号由前4号简正波合成。为了更好地看到时频分析的效果，仿真合成水声信号时认为各频率成分幅值相同，只考虑其相位特性。

比较图（1c）～图（1g）可以看出，短时傅立叶变换（STFT）虽然能够给出信号的联合时频特征，但其时频分辨率是固定不变的，而且其时频分辨率较低。频散短时傅立叶变换（D－STFT）是短时傅立叶变换（STFT）的1种改进方法，当信号频散程度不强，即不同频率到达时间相差不大时，时频分辨率同短时傅立叶变换相当（见图1c中的1号和2号简正波）；当频散明显时（见图1c中的4号简正波），不同频率信号到达时间相差较大，由于频散傅立叶变换考虑到频散特性，因而时频分辨率增强。

图（1d）可以看出，WVD的时频聚集性最好，然而，在频谱为0的地方，WVD并不为0，即有交叉项干扰。图（1e）中CWD的核函数是1个指数核，可以看到，交叉项被大大地抑制了，其时频分辨率虽优于STFT，但是比WVD降低了，而且核函数是固定的，不能随信号的不同而自适应变化。图（1f）给出的自适应最优核时频分析方法（AOK），相对于STFT、DSTFT，AOK分布的时频分辨率大大提高了；相对于WVD分布，交叉项被大大地抑制了；相对于CWD，AOK在抑制交叉项的同时，没有降低时频分辨率。不同频率的信号达到时间明显不同，呈现出明显的频散特性，高分辨率方法可以明显得到信号的频散曲线。

图1a 仿真海洋环境参数Fig.1a Simulated ocean environment parameter

图1b 水声仿真信号Fig.1b Simulated acoustic signal

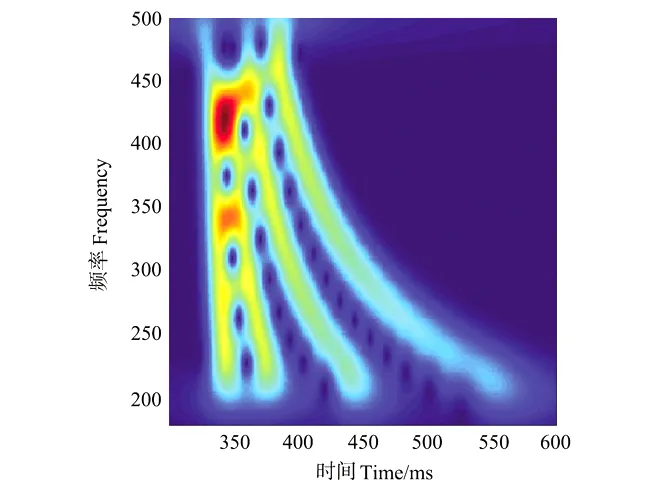
图1c 短时傅立叶变换（STFT）Fig.1c Short time Fourier transformation（STFT）

图1d 频散短时傅立叶变换（DSTFT）Fig.1d Dispersion short time Fourier transformation（DSTFT）

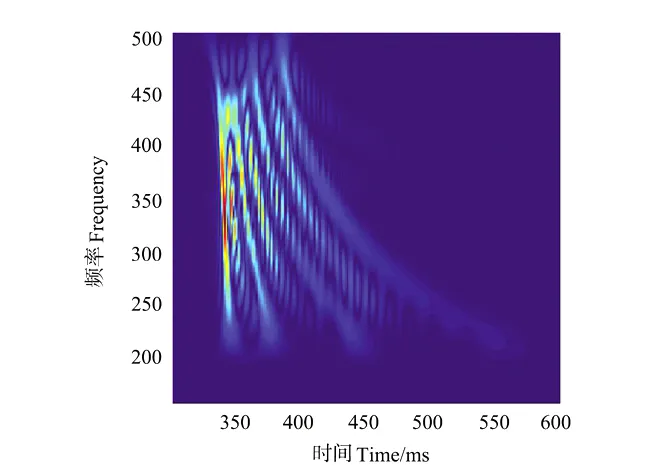
图1e Wigner分布（WVD）Fig.1e Wigner distribution（WVD）

图1f Cohen分布（CWD）Fig.1f Cohen distribution（CWD）

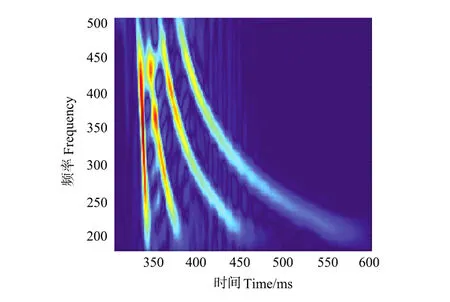
图1g 自适应最优核（AOK）Fig.1g Adaptive optimum kernel timefrequency representation

图2a 实验海域声速剖面Fig.2a The sound speed profile of experiment area

图2b 实验声压信号Fig.2b The experiment pressure signal

图2c 信号频谱Fig.2c Spectrum of signal

图2d 短时傅立叶变换（STFT）Fig.2d Short time Fourier transformation（STFT）

图2e 频散短时傅立叶变换（DSTFT）Fig.2e Dispersion short time Fourier Transformation（DSTFT）

图2f Wigner分布（WVD）Fig.2f Wigner distribution（WVD）

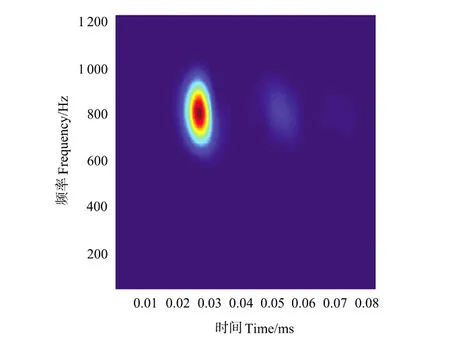
图2g Cohen分布（CWD）Fig.2g Cohen WVD（CWD）

图2h 自适应最优核（AOK）Fig.2h Adaptive optimum kernel timefrequency representation（AOK）

图2所示为2009年青岛崂山湾近海水声实验信号，采样率为12 000 Hz，其频谱图如图（2c）所示，信号带宽约200 Hz，能量主要集中在800 Hz附近。实验海域声速剖面如图（2a）所示。用STFT、DSTFT、WVD、CWD、AOK时频分布对该信号进行时频分析的结果如图（2d）～（2h）所示。可以看出：WVD、CWD、AOK时频分布的时频聚集性要好于STFT、DSTFT，WVD的交叉项干扰不明显，CWD的效果图与WVD的相差无几。AOK时频分布通过引入模糊函数实现对干扰项的滤除，在二维模糊域进行低通滤波，信号在通带，干扰项在阻带，通过自适应地调整低通滤波器来实现对干扰项的滤除，但该低通滤波器不是理想滤波器，在尽量滤除干扰项的同时，却降低了信号的时频分辨率，使AOK时频分布的时频聚集性低于WVD。

3 结语

水声信号的时频分布研究对目标定位、海洋声学参数反演的研究等等都具有重要的意义。高分辨率的时频分析方法可以更准确地刻画出频散特性，从而实现更精确地目标定位、更准确地计算海洋声学特性。本文通过比较短时傅里叶变换（STFT）、频散自适应短时傅里叶变换（DSTFT）、Wigner－Ville分布（WVD）、Cohen类时频分布（CWD）、自适应最优核时频分布（AOK）等方法，仿真和近海实验结果表明：WVD时频聚集性最好，但是有交叉项干扰；固定核函数的CWD较好地抑制交叉项，但弱化了时频聚集性；AOK时频分布在抑制交叉项和提高时频聚集性方面较好地折衷。

［1］ Gopu R Potty，James H，Miller Preston S，et al.Geoacoustic inversion using combustive sound source signals［J］.J Acoust Soc Am，2008，124（3）：146－150.

［2］ 张德明，李整林，张仁和.基于时频分析群延迟估计的海底参数反演［J］.声学学报，2000，30（5）：415－419.

［3］ 张学磊，李整林，黄晓砥.一种地声参数的联合反演方法［J］.声学学报，2009，34（1）：54－59.

［4］ 李亚军，王军，李刚虎.基于自适应高斯核函数时频分布的水声信号处理研究［J］.系统仿真学报，2006，18（11）：3230－3233.

［5］ 邹红星，周小波，李衍达.时频分析：回溯与前瞻［J］.电子学报，2000，28（9）：78.

［6］ Hong J C，Sun K H，KiMy Y.Dispersion based short－time Fourier transform applied to dispersive wave analysis［J］.J Acoust Soc Am，2005，117（5）：2949－2960.

［7］ Kwok H K，Jones D L.Improved instantaneous frequency estimation using an adaptive short－time fourier transform［J］.IEEE Trans on SP，2000，48（10）：2964.

［8］ Richard G Baraniuk，Douglas Jones.A signal－dependent time－frequency representation：optimal kernel design［J］.IEEE Transactions on Signal Processing，1993，41（4）：1589－1602.

［9］ Jones D L，Baraniuk R G.An adaptive optimal－kernel time－frequency representation［J］.IEEE Transactions on Acoustics，Speech and Signal Processing，1995，43（10）：2361－2371.

［10］ 王晓凯，高静杯，何洋洋.基于时频自适应最优核的时频分析方法［J］.系统工程与电子技术，2010，32（1）：22－26.

A Comparison of Time－Frequency Analysis Method and Their Applications to Underwater Acoustic Signal

YAO Yu－Ling，WANG Ning，SHI Hong－Hua，TAN Jun－Hong
（College of Information Science and Engineering，Ocean University of China，Qingdao 266100，China）

An acoustic wave in a shallow water ocean channel is proved dispersive.The dispersive property can be got by high resolution time－frequency analysis method.At present，there are a lot of time－frequency analysis methods.Short time Fourier transform（STFT），Wigner－Ville distribution（WVD），Cohen class distribution（CWD），adaptive optimum kernel time－frequency representation（AOK），Dispersionbased short－time Fourier transform（DSTFT）are studied in this paper.By using these methods to a simulated acoustic signal and an experiment signal and comparing the properties in time－frequency resolution precision，this paper draws the following conclusion：the time－frequency resolution precision of linear time－frequency representation including STFT is lower.Although the time－frequency resolution precision of WVD is excellent，its cross－terms are rather severe.CWD，the kernel function of which is exponential，can repress the cross－terms to a certain extent and its time－frequency resolution is better than STFT which is much lower than that of WVD.AOK time－frequency representation using adaptive kernel function is a relatively ideal method which can repress the cross－terms and has better time－frequency resolution.

WVD；adaptive optimum kernel；DSTFT

O427.2

A

1672－5174（2011）11－115－06

2010－10－20；

2011－06－10

姚玉玲（1974－），女，讲师。E－mail：yaoyuling2001＠ouc.edu.cn

责任编辑 陈呈超