地表水水质评价模型及其遗传算法求解

郑巧仙，刘金英，李明

（1.湖北大学数学与计算机科学学院，湖北 武汉430062；2.吉林大学数学科学学院，吉林 长春130012；3.武汉科技大学理学院，湖北 武汉430081）

地表水水质评价模型及其遗传算法求解

郑巧仙1，刘金英2，李明3

（1.湖北大学数学与计算机科学学院，湖北 武汉430062；2.吉林大学数学科学学院，吉林 长春130012；3.武汉科技大学理学院，湖北 武汉430081）

以标准等级水体为样本点构造样本空间，借鉴无单元思想，建立带权的地表水水质评价模型.对模型中的参数，根据数据拟合的思想，将问题转化为一个非线性优化问题，然后利用遗传算法进行求解.用已知算例对评价模型的合理性进行对比检验，并将其成功应用于密云水库样本点水质的综合评价，最后将此模型推广到一般情形的评价问题.

地表水水质评价模型；遗传算法；无单元

地表水水质评价是指根据地表水水体的各个要素检测值对水体进行综合评价，确定该水体所属的等级级别，常用的评价模型有神经网络模型、模糊综合评价模型、LOG模型、灰色理论评价模型等［1－3］，本文中以标准等级水体为样本点构造样本空间，借鉴无单元思想［4－5］，建立一种新的地表水水质评价模型，该模型不仅适应于地表水水质评价，而且对于一般的评价问题，只要给定评价标准，便能对其做出合理的评价.

1 地表水水质评价模型

1.1 标准等级水体样本空间的生成设地表水水体中标准水体空间所含点的个数为n，评价指标有m个，需要按L个级别进行评价，此标准水体关于这m项指标的标准值界限为已知.记λjk是第j（j＝1，…，m）个指标，属于第k（k＝1，…，L）类的上限（或下限）.对取值越大，级别越高的，指标λjk表示的是上限，对取值越小级别越高的，指标λjk则表示的是下限.设第i个水体的实测值为xi＝（xi1，xi2，…，xim），规定当第i个水体第j项指标的实测值x＊ij落入区间（λj，k－1，λj，k］时，第j项指标属于k级.

在每个指标相邻两类的限值区间内分别均匀生成n1组数据，得到n1L个样本x（k）l：

则x（k）l所对应的水质等级为y＊（x（k）l）＝k，其中k＝1，2…，L；j＝1，2，…，m；l＝1，…，n1L.

对L个边界λjk（j＝1，2，…，m；k＝1，2，…，L）各重复取n2组数据，得到n2L个样本：

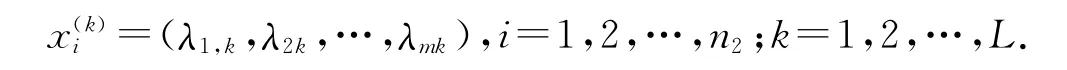
取其对应水质等级为

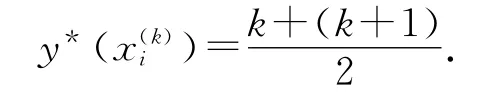
在标准等级之外的某个有限区间上各均匀取n3组数据，得到n3个样本.这样便得到一个含有n个已知水体质量等级的水体样本空间

1.2 地表水水质评价模型的建立记样本空间Ω＝（x＊1，x＊2，…，x＊n）中所有样本的第j个指标的样本均值为E（xj），样本均方差为sj.将样本数据及待评价水体xc的各项指标xcj分别归一化，有：

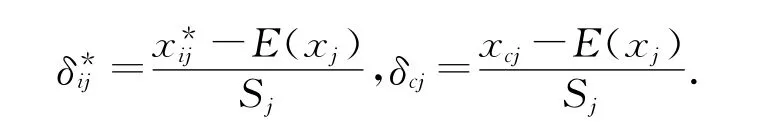
定义待评价水体xc与样本空间Ω的第i个水体x＊i的距离di为：

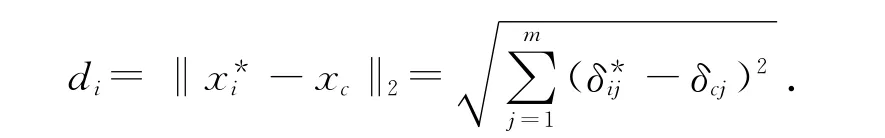
第i个样本水体对待评价水体xc的水质等级y（c）的贡献大小记为wi，借鉴无单元的思想将其定义为：

式中α≥1是待定参数，可通过对样本水体进行试验计算得到.于是得待评价水体xc的水质等级模型为：

2 利用遗传算法求解地表水水质评价模型中的参数

设M1≤α≤M2（M1、M2为参数α的估计值），对于样本空间中的任意一个水体x＊i，其对应的水体等级值为y＊（xi），而由其他n－1个水体根据（2）式计算出的等级值记作yc（xi），令

则显然参数α的取值应使得（3）式达到最小，于是得非线性优化问题：使得M1≤α≤M2.

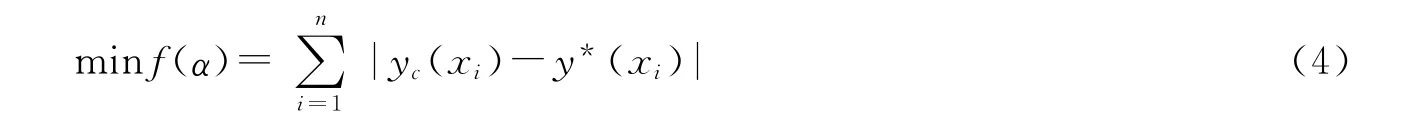
由于问题（4）的目标函数是个复杂的非线性函数，用传统的方法难以求解，而遗传算法［7－9］对目标函数的要求不高，易于求解此类问题.

遗传算法描述如下：

1）设置进化代数计数器t←0：在［M1，M2］内随机生成N个初始个体组成的初始群体P（t），并由（3）式计算得到各个个体的适应度Fi（i＝1，2，…，N）.

2）选择运算.对群体P（t）按最优保存策略进行选择运算，得到P1（t）.

3）交叉运算.对选择出的个体集合P1（t）作均匀交叉运算，得到P2（t）.

4）变异运算.对P2（t）作基本位变异运算，得到P3（t）.

5）终止条件判断.若不满足终止条件，则：更新进化代数计数器t←t＋1，并将第4）步中的P3（t）作为下一代群体P（t），然后转到2）；若满足终止条件，则：输出计算结果，算法结束.

3 地表水水质评价模型的检验

为检验模型（2）的有效性和可行性，将其与文献［6］进行对比，计算结果见表1.从计算结果看，模型（2）与LOG模型的评价结果一致；与神经网络模型相比，对东湖的评价结果偏高；与模糊综合评价模型相比，对西湖和东湖的评价偏高.总体上讲，与3种模型的评价结果基本一致，因此模型（2）可用于地表水水环境质量的评价.此外相较其他3种模型，本模型操作性更强，应用范围更为广泛.

表1 五大湖泊水环境质量等级评价结果

4 地表水水质评价模型在密云水库水质评价中的应用

密云水库是北京市区的主要供水源地，随着工农业的发展和人们生活方式的改变，密云水库的水体受到了一定程度的污染.为了对密云水库进行综合管理，我们对水库2002年丰水期若干监测点进行了采样，采样位置见图1，每个位置在不同的深度进行采样，采样数据见表2，由于各采样点的考察指标Zn变化不大，表2中没有给出其检测值）并就12项指标参照GB3835－2002地表水水质质量标准对其进行综合评价.根据地表水水环境质量标准值可以确定各项参数值分别为：m＝12，L＝5，λj，k（j＝1，2，…，m；k＝1，2，…，L）.依经验取n1＝15，n2＝5，n3＝5，n＝105，M1＝1，M2＝7.求解模型（4）所用遗传算法的各项参数见表3.

图1 密云水库采样位置示意图

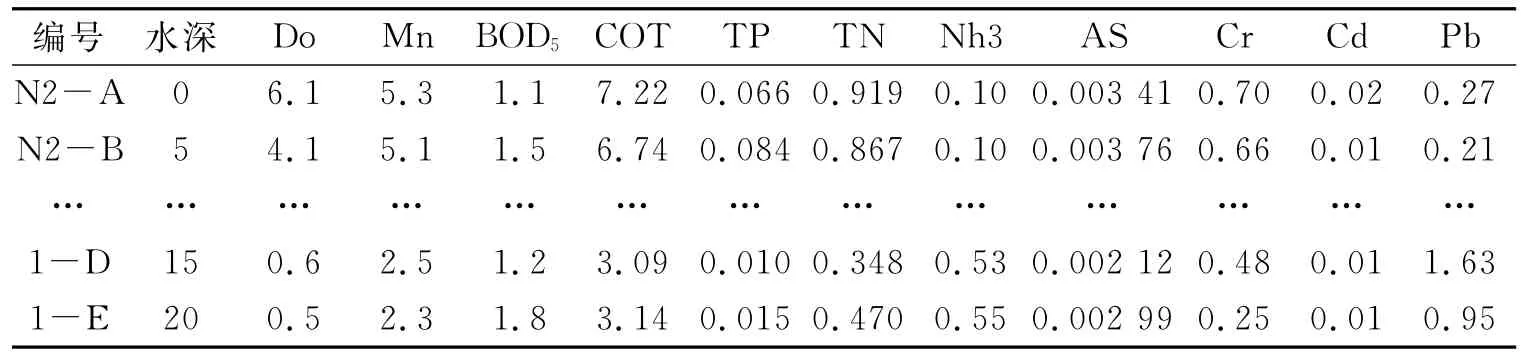
表2 2002年密云水库采样点的水质指标数据

表3 遗传算法中各项参数取值

表4 北京市密云水库采样点水质的综合评价值及其等级类别

利用遗传算法可求得问题（4）的最优解为α＝5.494 62，将其代入模型（2）可得密云水库各采样点的综合评价值及其所属等级类别见表4.计算结果表明，对同一地点不同深度的采样点，水位越深，水质越差；而对同一深度不同地点的采样点，河水入口点14、16的水质较差；水库中间的点4、5水质较好；大坝处的点19、6水质较差，这与实际情况基本上都是相吻合的.总的来看，密云水库的水质基本都属于二级水平，这为今后密云水库水质的进一步综合管理和规划提供了一定的理论依据.

5 结论

借鉴无单元思想，以地表水标准等级样本空间为基础，建立了地表水水质评价模型，并用改进的遗传算法对模型中所含的参数进行求解，得到了一种新的在水质评价中权的有效处理方法.该方法不仅仅适用于地表水水质评价问题，对任意一个评价问题，只要给出标准评价等级的样本空间，便可以利用文中的方法建立相应的评价模型，得到各样本点对待评价点的评价权值，从而对待价点进行评价.

［1］刘金英，杨天行，李明，等.一种加权绝对灰色关联度及其在密云水库水质评价中的应用［J］.吉林大学学报：地球科学版，2005，35（1）：54－58.

［2］郭彦英，邓云峰，任珺.AHP法在地表水水质综合评价指标权重确定中的应用［J］.兰州交通大学学报：自然科学版，2006，25（3）：70－76.

［3］马惠群，刘凌，陈涛.改进的多指标水质动态评价模型及应用［J］.武汉大学学报：工学版，2008，41（5）：54－58.

［4］周小平，周瑞忠.对无单元法插值函数的几点研究［J］.福州大学学报：自然科学版，2000，28（2）：52－56.

［5］王燕昌，李进.无单元方法的研究进展［J］.宁夏大学学报：自然科学版，2003，24（1）：42－46.

［6］金菊良，杨晓华，金保明，等.水环境质量综合评价的新模型［J］.中国环境监测，2000，16（4）：42－47.

［7］Holland J H.Adaptation in nature and artificial systems［M］.MIT Press，1992：12－55.

［8］周明，孙树栋.遗传算法原理及应用［M］.北京：国防工业出版社，1999.

［9］王小平，曹立明.遗传算法：理论、应用与软件实现［M］.西安：西安交通大学出版社，2000.

The estimate model designed for the surface water quality and its solution with a genetic algorithm

ZHENG Qiaoxian1，LIU Jinying2，LI Ming3
（1.School of Mathematic and Computer Science，Hubei University，Wuhan 430062，China；2.School of Maths，Jilin University，Changchun 130012，China；3.Collge of Sciences，Wuhan University of Science and Technology，Wuhan 430081，China）

The estimate model with weights for the surface water quality was set up，using for the idea of naught unit based on the sample space structrued with standard level of water samples.The parameter problem of the model could be transformed into a nonlinear optimization problem using for the idea of data fitting.The genetic algorithm was used to solve the weight of the model.A contrast test was done to check up the rationality of the model with an eaemple，and the model was applied successfully in the evaluation of sample point of Miyun reservoir.At the last，the model was promted to the general evaluation problems.

the estimate model of surface water quality；genetic algorithm；naugth unit

X 824

A

1000－2375（2011）04－0475－04

2010－05－24

国家自然科学基金（60603069）和湖北省自然科学基金项目（2009CDB144）资助

郑巧仙（1978－），女，讲师，E－mail：zqxlm1978＠163.com

（责任编辑 赵燕）