钢液内宏观超声空化特征的数值模拟

孔 为，苍大强，王文波（北京科技大学冶金与生态工程学院，北京 100083）

钢液内宏观超声空化特征的数值模拟

孔 为，苍大强，王文波（北京科技大学冶金与生态工程学院，北京 100083）

本文基于CFD软件FLUENT，通过编写UDF来模拟钢液内由于超声波振动所产生的空化特征。结果表明：未加空化模型的钢液流场内存在正负压，分别可达到5.5MPa和－5.4MPa；加入空化模型的钢液流场内只存在正压，且压力值显著减小，最大值稳定在0.10MPa～0.12MPa，最小值稳定在0.08MPa～0.1MPa。两者变化趋势正相反。每一时刻都有一部分钢液区域不析出气体。加入空化模型后压力积分值变化曲线位置随时间小幅度增高，含气率积分值曲线变化趋势与此正相反。各亚松弛因子的变化对空化模拟计算结果的精确度产生的影响不大。湍流动能、湍流耗散率、密度和体积力等亚松弛因子对低压流体比较敏感。改变湍流模型和壁面函数对空化模拟计算结果基本无影响。不可压缩气体的存在有利于空化作用的产生。

钢液；超声波；空化；数值模拟

超声波能量足够高时，就会产生“超声空化”现象。对于空化现象的研究主要包括实验研究[1]和数值模拟研究[2～5]。但主要集中在对水[1～5]及低熔点合金熔体[6]方面。关于空化对钢液的方面，主要研究空化作用所产生的良好效果[7，8]，诸如改善钢的凝固组织，均匀成份，改善夹杂，从而提高钢的力学性能。对钢液本身的空化特征研究尚属空白。本文对钢液内宏观超声空化特征进行数值模拟研究，为进一步的试验研究及超声波引入到钢的生产中提供一定的理论指导。

1 数学模型

模拟对象为刚玉坩埚中的钢液在超声波处理振动下的压力场及空化场变化。坩埚尺寸为ø55（内径）mm×120（内高）mm，壁厚为3mm。工具头材质为Mo－Al2O3－ZrO2金属陶瓷管[9]。超声波处理采用上部导入法，工具头从上部直接插入钢液内进行施振，液面高度为54mm。超声波发生器工作频率为20kHz。

1.1 计算假设

（1）假设整个模拟过程为绝热的，不考虑热对流的影响；

（2）假设钢液为不可压缩流体；

（3）忽略空化气泡崩溃所产生的喷射流；

（4）假设金属陶瓷管的物理属性与刚玉相同。

1.2 主控方程

因为模型可简化为二维轴对称模型，于是相应的主控方程分别为：

连续性方程

式中：u、v——分别为极坐标系下轴向（x）、径向（r）2个方向上的速度分量；

ω——漩涡速度，m/s；

p——压强，Pa；

Sx、Sr——极坐标轴轴向、径向2个方向上的动量源分量（本研究中为 0），N/m3；

ρ——密度，kg/m3；

μ——动力粘性系数，单位为Pa·s。

1.3 定解条件

建立的计算区域模型如图1所示。选用非定常求解器，计算0.2ms。湍流模型选择标准k-ε模型；模型中的坩埚壁及工具头壁（材质均为默认的刚玉）均采用无滑移边界条件，在近壁区采用标准壁面函数；出口条件为压力出口；工具头端面为动边界，结合前述超声波发生器工作参数，设置动边界的位移方程为：

式中a=10μm，f=20kHz，t为超声波发生器作用时间。将式（4）结合超声工作参数通过编写UDF程序加入到Fluent动网格设置选项中。加入空化模型的同时，采用多相流混合物模型。Fluent所采用的空化模型为Singhal等所发展的完全空化模型[10]。物性参数为：钢液的密度为 7000kg/m3，动力粘性系数为 6.1·10-3Pa·s；钢液内气体密度为1.225kg/m3，动力粘性系数为1.8·10-5Pa·s；气化压强为 6Pa。

2 计算结果与讨论

2.1 流场计算结果与讨论

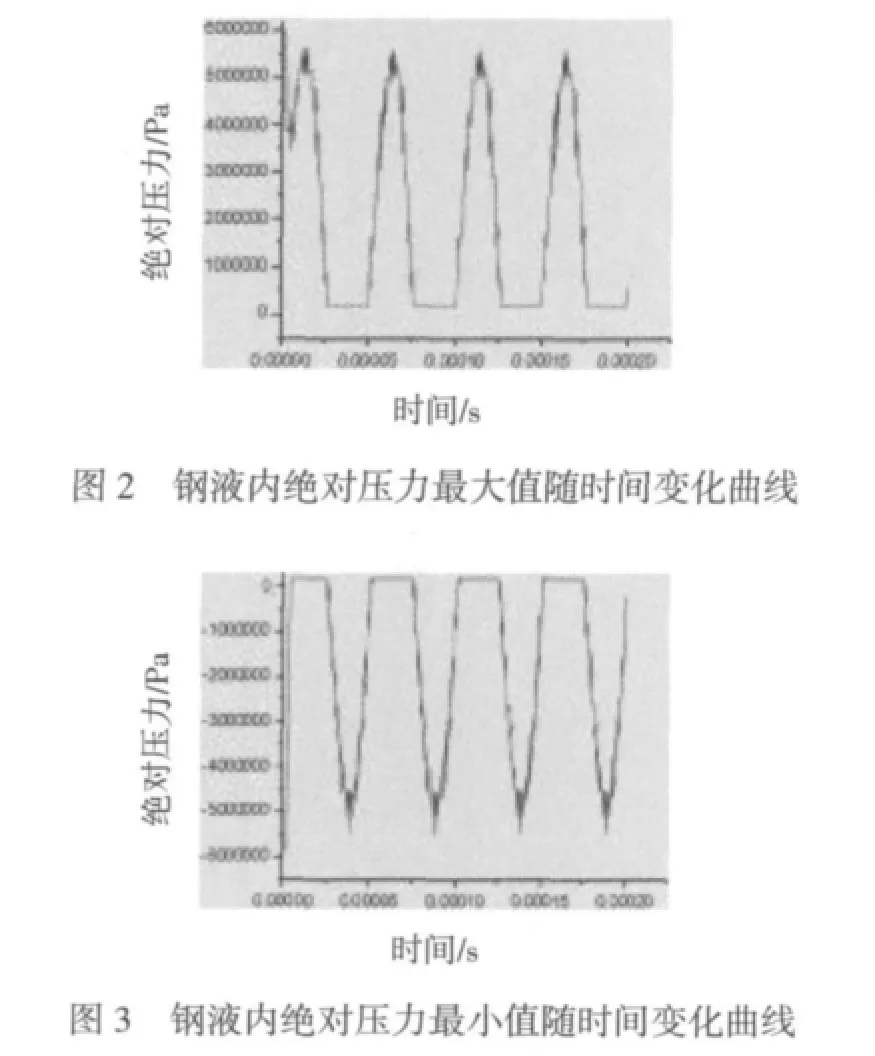
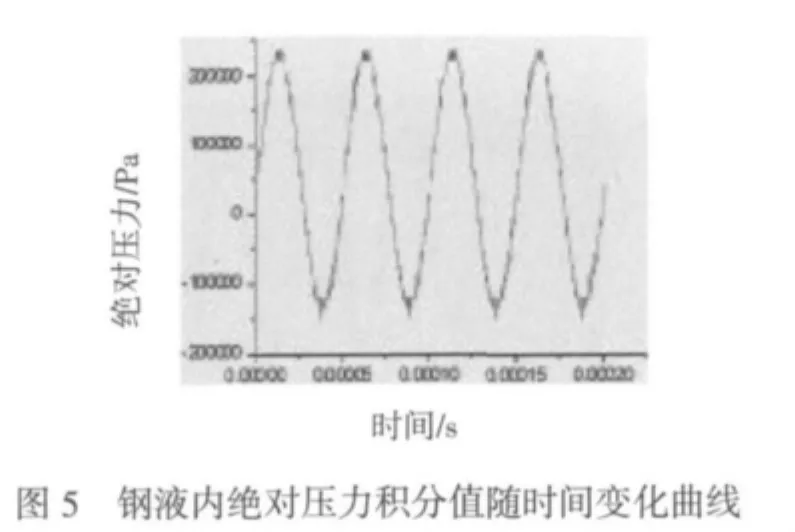
为了研究超声波振动产生的空化作用与不考虑空化作用对钢液内流场影响的不同。首先排除钢液内次相——气体的影响，先不加入空化模型。步长为0.5μs，经过400步迭代，得出钢液内绝对压力最大值（如图2）和最小值（如图3）随时间的变化情况。可以看出，振动过程中钢液内绝对压力变化有很明显的规律性。由于工具头端面的振动频率是20kHz，振动周期就是0.5×10-4s，所以在迭代400时间步数，0.2ms中运行了4个周期。钢液内压力最大值和最小值变化也符合这个振动周期。绝对压力出现了负压，正负压的幅值很大，达到了5.5MPa和-5.4MPa。当压力最大值达到最高时，压力最小值也为最高值。当压力最小值达到最低时，压力最大值也达到最低值。二者变化趋势一致。负压的出现使钢液内局部压强低于液体的饱和蒸气压（气化压强），就可以产生空化现象。图4为计算出的不同时刻压力云图。可发现迭代到25步时压力最大值达到峰值，且分布在工具头端面下一个很小的区域，压力由这个小区域向外呈辐射状减小。随着迭代时间步数的增加，压力整体变小，但原来相对高压区域的压力降低速率高于相对低压区域压力降低速率。以致迭代到75步时，原压力最大值峰值区域变成压力最小值峰值区域，同样压力由这个压力最小值峰值区域向外呈辐射状增大。迭代步数继续增加，压力整体变大，但原来相对低压区域压力增高速率高于相对高压区域压力增高速率。以致迭代到125步时，压力分布情况重新回到迭代到25步时的情况。继续迭代，压力分布情况如前述循环变化。为了评价钢液整体的压力情况，计算出随时间变化的钢液内绝对压力积分值变化曲线，如图5。可看到明显的正弦曲线，完全符合前述的振动周期特征。压力积分值最大值和最小值的出现时刻符合前述压力最大值和压力最小值变化趋势。

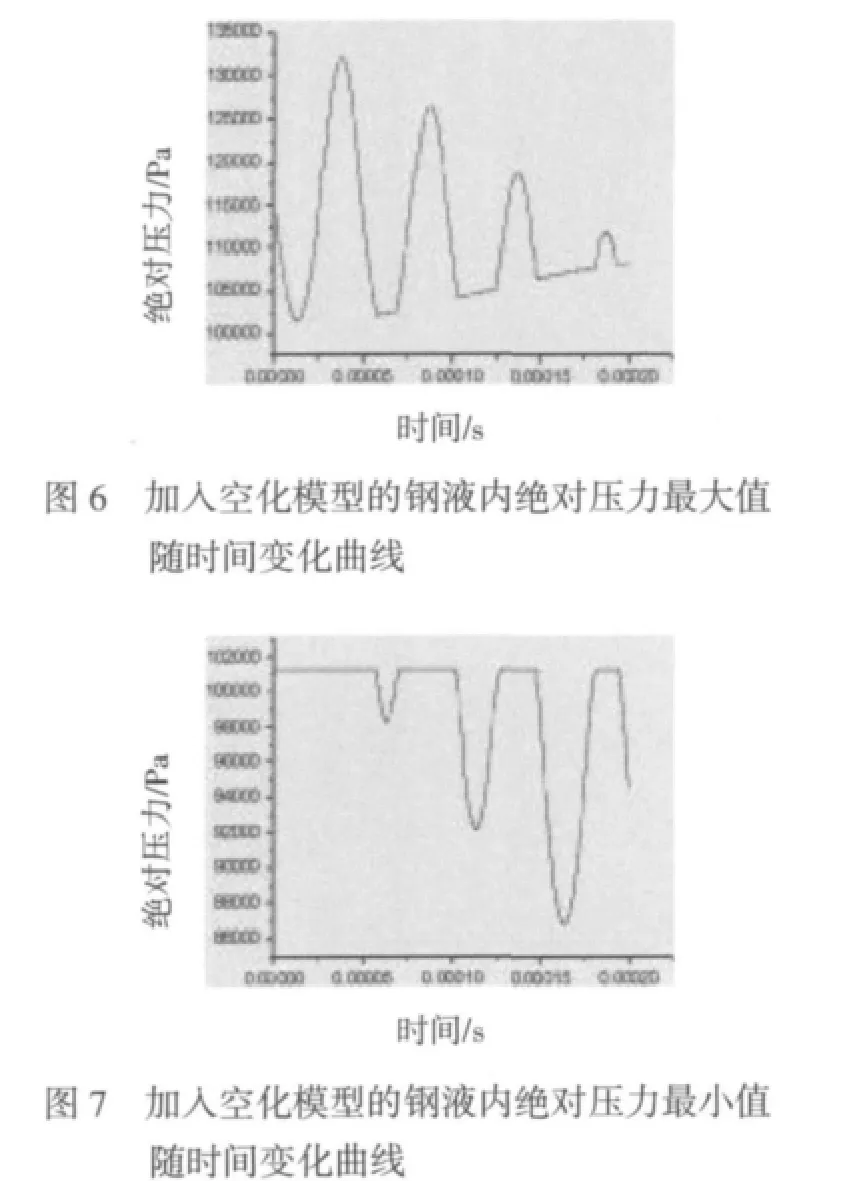
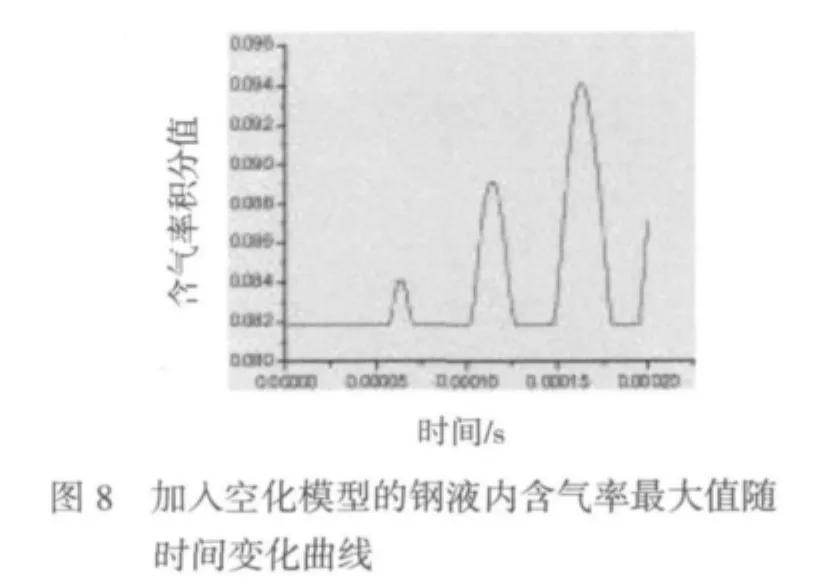
加入空化模型后，同样采用步长为0.5μs，先迭代400时间步数，计算出钢液内绝对压力的最大值（如图6）和最小值（如图7）随运行时间变化的曲线。可看出两曲线中的压力全部为正压，压力幅值较未加空化模型时大幅降低，且曲线的周期与前述相同；曲线更加圆滑，这说明空化模型的加入可以优化计算结果；压力最大值变化曲线振荡幅度随时间减小。进一步延长迭代时间步数，发现曲线的振动幅度随时间在减小到一定程度后，又逐渐增大，最后振动幅度稳定到0.10MPa到0.12MPa之间。在400时间步数内，压力最小值变化曲线振荡幅度随时间逐步增大。进一步延长迭代时间步数，发现曲线的振动幅度随时间在增大到一定程度后，又逐渐减小，最后振动幅度稳定到0.08MPa到0.1MPa之间。图8为迭代到400步时，随时间变化钢液内含气率最大值的变化曲线，可看到此曲线的变化规律与压力最小值的变化规律完全相反，进一步延长迭代时间步数，可知最后曲线振动幅度稳定在0.08到0.1。计算得出的各个时刻最小含气率均为0，这说明每一时刻都有一部分钢液区域不析出气体。计算出不同时刻的压力云图和气化率云图，可发现，与图4相似，也存在分布在工具头端面下的压力最大值峰值区域和压力最小值峰值区域，整体压力随时间变化情况与未加空化模型时基本一致，但峰值区域外的其他外围区域压力分布较为均匀，不存在压力变化的辐射状分布。空化区域随时间的分布变化情况与压力分布变化情况正相反。为了评价加入空化模型后的钢液整体的压力及空化情况，计算出钢液内绝对压力积分值变化曲线，如图9，及含气率积分值变化曲线，如图10。与未加空化模型的压力积分值变化曲线相比，加入空化模型后压力积分值变化曲线位置会随时间整体小幅度增高；含气率积分值变化曲线与压力积分值变化曲线的变化规律正相反，曲线整体位置随时间小幅度降低。

2.2 计算参数的影响与讨论

通过改变算法及物性参数，可以研究其对加入空化模型的数值模拟计算结果的影响。本文主要研究4种参数的改变对计算结果的影响：①亚松弛因子；②湍流模型；③壁面函数；④不可压缩气体的质量分数。

首先考虑亚松弛因子的改变，不同的亚松弛因子组合列入表1。

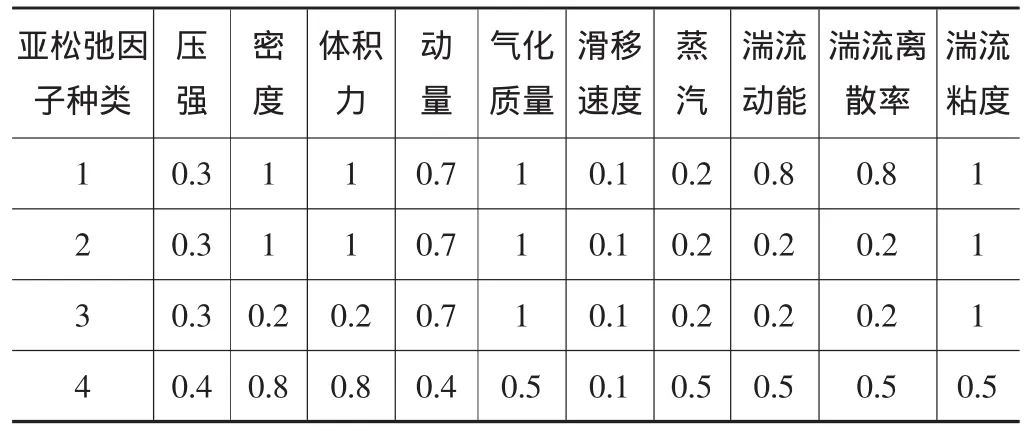
表1 亚松弛因子的不同组合

图11为迭代到125步时，不同亚松弛因子组合的绝对压力云图。可清晰地看到4组压力分布均较为合理，但2、3、4组图中的中心靠左下位置均出现两块三角形白色区域，这说明此处计算失真。可见各亚松弛因子的变化均会对计算结果的精确度产生一定的影响，但影响不大。系统默认的亚松弛因子组合，即第一组为最佳组合。另外各组压力最低值大小比较情况为：1=4>2>3。这说明2组（即湍流动能、湍流耗散率等亚松弛因子）及3组（即密度、体积力等亚松弛因子）对低压流体比较敏感，更易产生空化气泡。

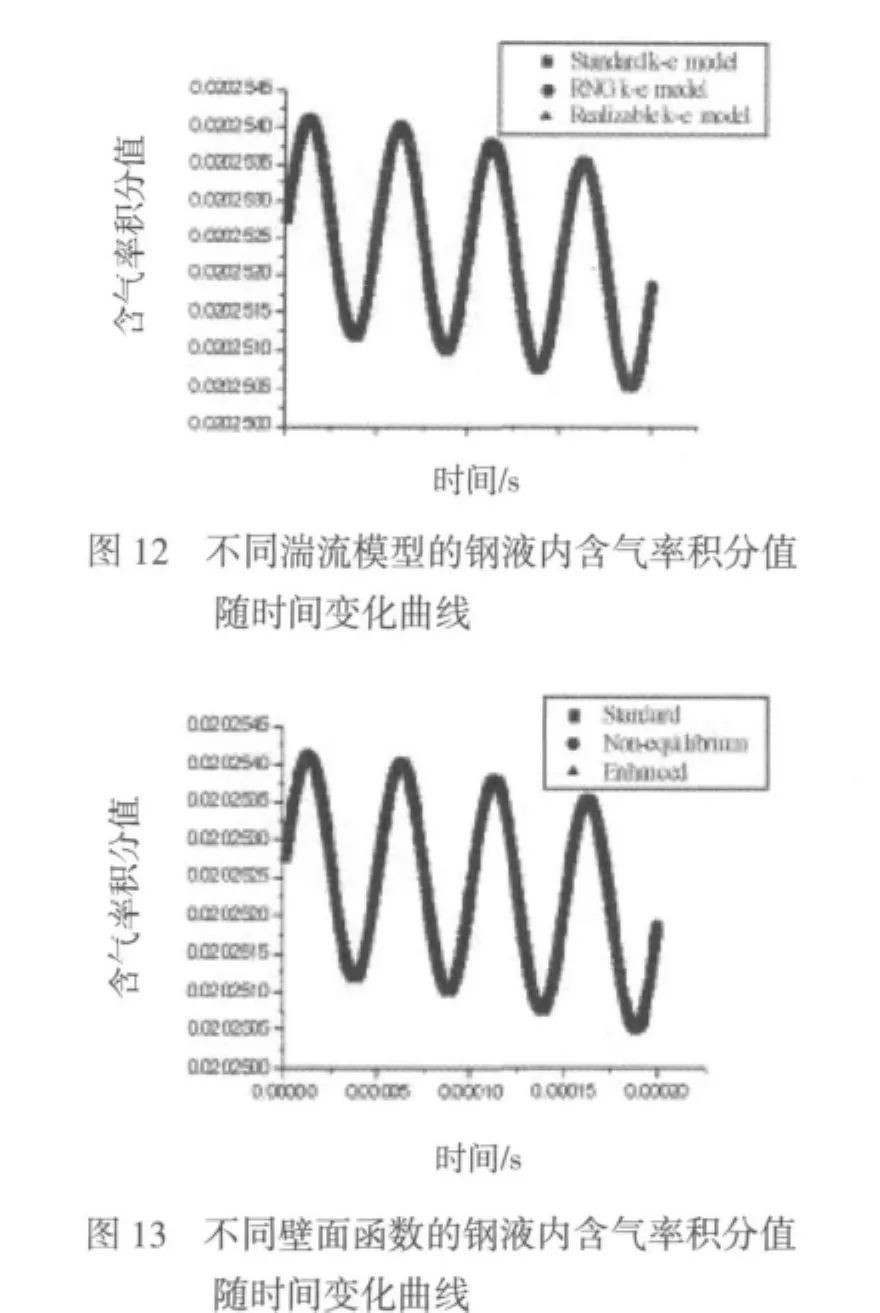
考虑3种不同湍流模型对计算结果的影响：（1）Standard k-ε 模型；（2）RNG k-ε 模型；（3）Realizable k-ε模型。其中Standard k-ε模型只适合完全湍流的流动过程模拟；RNG k-ε模型是针对高雷诺数流动问题的；Realizable k-ε与标准k-ε模型相比有2个主要的不同点，即Realizable k-ε模型增加了湍流粘性和为耗散率增加了传输方程，这个方程用于处理层流的速度波动。另外由于空化在工具头端面附近区域有较强的集中性，因此选择何种壁面函数，也可能会影响空化模拟的计算结果精度。同样考虑三种不同壁面函数：（1）Standard；（2）Non-equilibrium；（3）Enhanced。为总体反映各模型及各壁面函数对计算结果的影响，均采用计算迭代到125步时各种模型的含气率积分值作为评价标准。图12为3种模型的随时间变化的含气率积分值变化曲线。图13为3种壁面函数随时间变化的含气率积分值变化曲线。可看出两图中的三条曲线均完全重合，这说明这三种模型及三种壁面函数对计算结果基本无影响，对一般的钢液内空化模拟问题计算都有较好适应性。

液体中往往存在不可压缩气体。即使不可压缩气体质量分数的微小变化也会对模拟的结果产生很大的影响。先迭代400步，考虑在三组不同不可压缩气体质量分数情况下，对钢液内计算结果的影响。三组不可压缩气体质量分数取值分别为 10-2、10-5、10-8。图14为这三种不同情况所计算出的含气率积分值曲线。图14（1）为三种情况的曲线合图，可看出随着不可压缩气体质量分数的增加，含气率也有明显的提高，而含气率的增高比例远大于不可压缩气体质量分数的增加值，这说明不可压缩气体的存在有利于空化作用的产生，提高空化比例。从图14（2）、图 14（3）中，可看出：当不可压缩气体质量分数为10-2和10-5时，这两种的情况的含气率变化曲线整体形状改变不大；然而当不可压缩气体质量分数降低为10-8时，如图14（4），曲线形状发生很大变化，含气率变化不再有正弦周期，而是随时间逐渐变大；增加迭代步数后，发现含气率不再一直增大，也无明显变化规律，但最高为0.001。

3 结论

（1）未加空化模型的钢液流场内存在正负压，正负压分别可达到5.5MPa和-5.4MPa，且压力变化带有一定的周期性，周期性符合超声波工作参数。

（2）加入空化模型的钢液流场内只存在正压，且压力值较未加空化模型时显著减小。压力最大值稳定到0.10MPa到0.12MPa之间，压力最小值稳定在0.08MPa到0.1MPa之间；两者的变化趋势正相反。每一时刻都有一部分钢液区域不析出气体。压力积分值变化曲线位置随时间整体小幅度增高，含气率积分值曲线变化趋势与此正相反。

（3）各亚松弛因子的变化会对空化模拟计算结果的精确度产生一定的影响，但影响不大。湍流动能、湍流耗散率、密度和体积力等亚松弛因子对低压流体比较敏感。

（4）改变湍流模型和改变壁面函数对空化模拟计算结果基本无影响。

（5）不可压缩气体的存在有利于空化作用的产生，提高空化比例。

[1]王国刚，孙冬柏，张秀丽，等.空泡溃灭过程中力学损伤行为[J].北京科技大学学报，2007，29（5）:483-485.

[2]Kim J O，Choi S，Kim J H.Vibroacoustic Characteristics of Ultrasonic Cleaners[J].Applied Acoustics，1999，58（2）:211-228.

[3]Dubus B，Granger C，Mosbah P，et al.Numerical Modeling of the Ultrasonic Cavitation Field and Experimental Evaluation of Bubble Density[A].Proceedings of the 3rd Conference on the Applications of Power Ultrasound in Physical and Chemical Processes[C].Sevilla:Sociedad Espaňola de Acústica，2001:169-174.

[4]Kaltenbacher M，Land-H，Hoffelner J，et al.Use of Modern Simulation for Industrial Applications of High Power Ultrasonics[A].Proceedings of the IEEE Ultrasonics Symposium[C].München:IEEE，2002:673-678.

[5]Lewis J P，Gardner S，Corp I.3D.Simulation of an Ultrasonic Cleaning Vessel-Modelling Methodology and Practical Comparisons[A].In Anglo-French Physical Acoustics Conference [C].Kent:Institute of Physics，2006:1-4.

[6]刘荣光，李晓谦，胡仕成.铝合金熔体中超声空化效应和气泡运动过程模拟[J].开发研究，2007（6），16.

[7]李杰，陈伟庆.超声波熔体处理对高碳钢凝固组织和性能的影响.铸造，2008，57（10）：1009-1011.

[8]李杰，陈伟庆，王晓峰.超声波功率对高碳钢中夹杂物的影响.北京科技大学学报，2009，31（9）：1112-1121.

[9]李杰，陈伟庆，何北星，等.超声波处理高温钢液工具头材质的选择研究[J].北京科技大学学报，2007，29(12)：1246-1249.

[10]A K Singha，l H Y L，i M M Athavale，et a.l Mathematical Basis and Validation of the Full Cavitation Model [J].Journal of Fluid Engineering，2002，124：617-624.

Numerical Simulation of Macroscopic Ultrasonic-Cavitation Features in M olten Steel

KONG Wei，CANG DaQiang，Wang WenBo
（School of Metallurg ical and Ecolog ical Eng ineering，University of Sience and Technology Beijing，Beijing 100083，Beijing China）

The research has been based on CFD software Fluent and cavitation features generated by ultrasonic vib ration in m olten steel have been sim ulated through p rog ramm ing UDF.Results showed that w ithout cavitation model,positive p ressure and negative p ressure were p resent in molten steel and positive p ressure reached 5.5Mpa while negative p ressure-5.4Mpa；w ith cavitation model,there was only positive p ressure and the p ressure value decreased obviously.Maximum value of p ressure stabilized the value between 0.10Mpa and 0.12Mpa.Minimum value of p ressure stab ilized the value between 0.08Mpa and 0.1Mpa.Changes of maximum value of p ressure had a contrary trend w ith changes of m inimum value of p ressure.In every moment,there were som e reg ions w ithout separating out gas in m olten steel.With cavitation model,curve of variations of integral value of absolute p ressure increased slightly,and variations of gas volum e frac tion had a contrary trend w ith variations of integ ral value of absolute p ressure.Underrelaxation factors had some effects on accuracy of calculation results of cavitation simulation though the effec ts were small.Turbulent kinetic energy,turbulent d issipation rate,density and body forces were sensitive to low-p ressure fluid.Changes of turbulent model and wall function had no effects on calculation results of cavitation simulation.No-condensab le gas in existence could be infavor of p roducing cavitation.

Molten steel；Ultrasonic；Cavitation；Numerical simulation

T P391.9;

A；

1006－9658（2011）02－5

2010－10－15

2010－152

孔为（1983－），男，博士研究生