偏肥尾分布的APARCH模型研究

张家平

(1.华南理工大学 金融工程研究中心，广州 510006;2.华侨大学 数量经济研究院，福建 泉州 362021)

偏肥尾分布的APARCH模型研究

张家平1，2

(1.华南理工大学 金融工程研究中心，广州 510006;2.华侨大学 数量经济研究院，福建 泉州 362021)

金融收益率时间序列分布的不对称性已被视为金融市场的一个“典型事实”，但现有文献对金融时间序列偏度的关注相对较少。由于受到估计方法和计算效率的约束，波动率模型通常假定条件分布为正态分布或对称肥尾分布，如t分布和广义误差分布，偏度建模比肥尾建模要复杂得多。通过运用芬南德兹—斯蒂尔方法，在对称分布的基础上构造出有偏肥尾分布。在假定APARCH模型的残差项服从这种偏肥尾分布的情况下，研究波动率的拟合效果与预测能力。实证结果显示，与残差项服从对称分布的波动率模型相比，有偏性对波动率模型的估计和预测都有显著影响，向前预测的步数越多，影响越明显。

条件分布;APARCH;肥尾分布;时间序列

一、前 言

波动率是金融资产定价和风险管理的关键输入变量，波动率建模是定量金融中一个非常活跃的研究领域。金融资产收益率的经验分布显示出众所周知的特征，即典型事实，包括波动聚集、尖峰肥尾和杠杆效应。波动率建模就是要充分刻画这些特征。由恩格尔提出的标准ARCH模型和伯勒斯勒夫进一步扩展的GARCH模型，能较好刻画上述部分典型事实而成为刻画波动率最受欢迎的模型。标准的ARCH和GARCH模型可以构造尖峰肥尾的无条件分布，但不能消除条件分布的尖峰肥尾［1］，即扰动项偏离正态分布，而且不能描述冲击的杠杆效应等吸引了大量学者对该模型进行改进和拓展。

一般沿着两个方向进行来改进GARCH模型。一是改进条件均值方程和条件方差方程的设定。斯瓦特提出了TS－GARCH模型［2］，格罗斯特恩等人提出了GJR－GARCH模型［3］，黑金斯和波拉提出了N－ARCH模型［4］，扎克恩提出了T－ARCH模型［5］，这些模型通过改变条件方差方程的设定，使之能反映杠杆效应。杰维克提出的Log－ARCH模型［6］，使得波动率总是满足为正的条件。而我们考察的是更为一般的，并包含上述模型设定形式的APARCH模型［7］。二是采用非正态分布刻画扰动项的尖峰肥尾。条件均值方程的扰动性偏离正态分布，一个自然的拓展就是采用肥尾分布来构建GARCH模型。文献中运用最广泛的肥尾分布是伯勒斯勒夫对扰动项引入的学生t分布和尼尔逊采用的广义误差分布(GED)［8～9］。①研究者尝试采用了很多其他分布形式，如双指数分布、双Weibull分布、双曲分布等，有兴趣者可参考Bond(2000)的文献综述。但这些分布都是对称分布，不能刻画金融收益率分布的不对称性。芬南德兹—斯蒂尔提出对于任何连续、单模式和对称的分布f(z)，可以通过改变分布两边的尺度(scale)来引入有偏性，从而构建出偏正态分布、偏t分布和偏GED分布［10］。坎贝尔和汉森构建偏 t分布来刻画条件偏度［11～12］，实证研究发现引入条件偏度非常重要并会影响条件方差的可持续性。哈维和斯蒂克研究了条件偏度对资产定价的影响，建议把条件偏度作为一个定价风险因子［13］。

我国学者对金融资产收益率的条件分布进行了比较研究。高见有对残差项分别服从正态分布、t分布和GED分布的GARCH模型进行对比分析，发现 t的拟合较好［14］。李聪比较GARCH、EGARCH和PARCH在上述三种分布下的估计，并用于计算 VaR，发现GED分布较好［15］。魏宇等考察了在正态分布、偏正态分布、GED和偏GED下随机波动率模型的估计与拟合检验，发现 GED和偏 GED效果较好［16］。目前还没有文献系统考察条件偏度对波动率预测的影响和实证研究引入条件偏度后对条件波动率预测的改进。

二、模型设定

1.偏分布的构造

芬南德兹和斯蒂尔提出一种构建偏分布相当一般化的方法，对于任何连续、单模式和对称的分布f(z)，可以通过改变分布两边的尺度来引入有偏性［10］。

其中，0<β<∞是偏度参数，反映分布偏斜的方向和程度。β=1生成对称分布，即f(z|β=1)=f(z)，β<1时右偏，β>1时左偏。偏分布的各阶矩决定于原对称分布的各阶矩Mi和β，计算方法如式(2)。

根据式(1)和式(2)，我们可以构建 sT、SGED等偏分布并计算其各阶矩。以GED为例，②SN、ST的构造方法类似，为节省篇幅，本文不列出。由于正态分布不能刻画肥尾，一般不采用SN。标准广义误差的密度函数表示如下:

其中，0<υ≤(为形状参数，控制GED的高度和肥尾。υ=2时GED退化为正态分布，υ=1时为Laplace分布，υ→(时是区间为［－2，2］的均匀分布，υ<2时为尖峰分布，υ>2时为宽峰分布(platykurtotic)。

由式(1)构造标SGED的密度函数表示为:

形状参数υ与GED的相同，偏度参数β>0，当υ=2和β=1时，SGED退化为正态分布。

2.APARCH(p，q)模型设定

另一种金属盐——硫酸铜也可作安全的蚀刻剂使用，主要用于腐蚀锌版和铝版。其腐蚀原理与氯化铁类似，如以锌版蚀刻为例：

在GARCH模型的框架下，Ding和Granger等人对条件方差方程的设定如下，

其中，δ>0，参数γi反映冲击的杠杆效应，如果γi大于0(或小于0)，说明负冲击比正冲击的效应要大(或小)。Dθ(0，1)表示扰动项或残差项的标准条件分布，θ是控制分布偏度和峰度的参数。当 ω >0，∑iαiκi+ ∑jβj<1，其中 κi=E(|z|+γiz)δ时，稳定解存在。当 γ≠0和 δ≠2时，κi值取决于扰动项分布的假设。

APARCH模型包容性很强，许多其他GARCH类模型都是APARCH模型的特例，对应关系如表1所示。

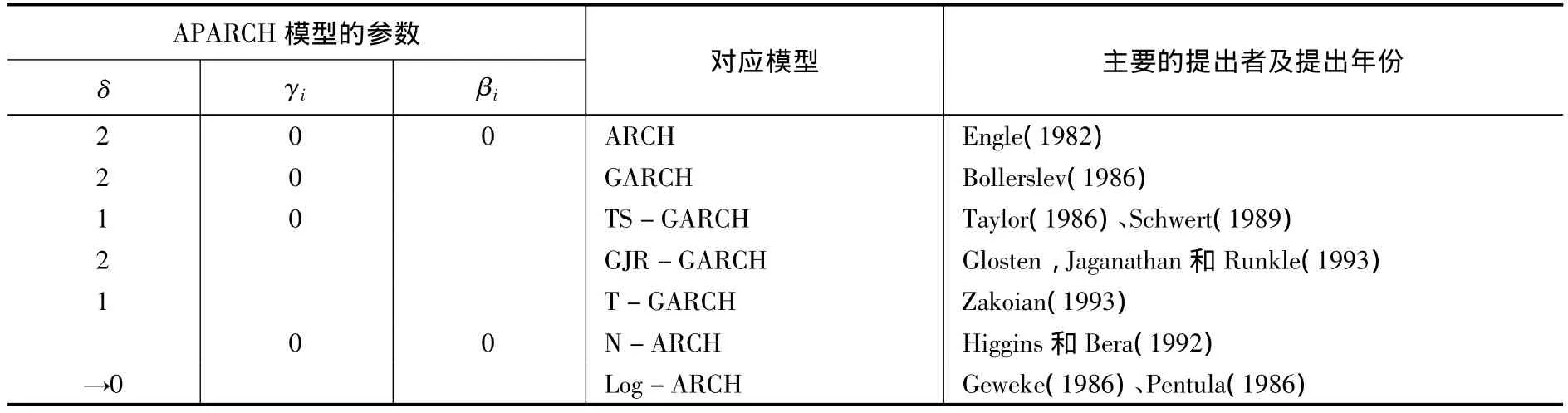
表1 APARCH模型与其特例的对应关系

三、实证分析

1.数据来源与统计分析

本文实证分析的数据是上证综指1997年1月2日至2009年9月30日的日指数价格，共3059个观测值。我们采用指数价格对数的一阶差分作为连续复利收益率。从图1可以看出，指数价格从2006年开始上升，在2007年10月下跌，持续整个金融危机期间，收益率序列具有显著的波动时变性和聚集性，在危机期间，波动显著增强;对收益率序列进行统计分析，分析结果如表2所示。

表2 指数收益率统计分析结果

从表2可以看出，收益率的平均值为正，但接近于0。最大值和最小值反映了涨跌停板制度对波动的限制。收益率分布不是对称的，偏度为负说明落在左尾部的观测值要比右尾部的多。峰度是正态分布的2倍多，表示经验分布存在“尖峰肥尾”典型事实。

为考察收益率序列是否为平稳的，我们进行ADF检验，估计结果对应的p值几乎为0，拒接序列存在单位根。LM检验发现收益率存在显著的ARCH效应。

2.条件分布为ST、SGED的APARCH模型的参数估计及分析

我们分别用ST、SGED来刻画条件均值方程残差分布的有偏、肥尾等特征。利用最大似然法，我们可以估计 APARCH－ST、APARCH －SGED模型的参数，包括条件分布的参数。为进行模型比较，我们还估计出常用的基于 N、t、GED的APARCH模型，结果见表3。

表3 不同分布假定下模型的估计结果

从表3可以看出，一是通过对各模型的标准化残差的诊断检验，APARCH(1，1)设定充分消除了收益率序列的系列相关和ARCH效应，而且各模型均满足∑iαiκi+ ∑jβj<1，说明条件方差是平稳的。二是除均值项μ外，其他参数都在1%置信水平下是统计显著。三是APARCH－ST和APARCH－SGED的偏度参数(分别为0.9281、0.9181，均小于1，说明标准化残差分布是左偏的。这与样本偏度－0.2105的结果是一致的。四是我们根据对数似然值和信息准则来进行模型比较，在不同分布假定下，APARCH－ST模型的似然值最大，AIC和BIC值最小，说明该模型在五个模型中拟合效果最好。同时基于ST和SGED假定的模型拟合效果均优于基于对称分布的模型效果，说明引入有偏性对模型拟合效果的改进是显著的。

标准化残差的密度函数曲线见图2，为便于进行比较，我们还画出相应的对称分布和正态分布图。从图2可以看出，偏分布的左尾比对照分布的左尾更厚，能更准确的刻画金融风险。

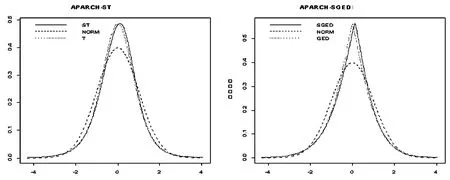
图2 标准化残差的密度函数、相应的对称分布和正态分布的密度函数图

3.波动率预测及预测效果比较

预测是研究波动率模型的主要目的之一。根据表3，对称分布中，APARCH－T的拟合效果最好，因此我们选择APARCH－T、APARCH－ST和 APARCH －SGED，分别进行 1、2、5、10、20 步预测，并根据均方根误差和平均相对误差来比较各模型的预测效果。计算结果如表4所示。

表4 各模型预测误差估计表

从表4可以看出，根据均方根误差，APARCH－T在进行1、2、5步预测时误差最小，而APARCH－SGED在进行10、20步预测时是最优的;根据平均相对误差，除APARCH－T在1步预测是最优的外，其他预测都是APARCHSGED最优。这说明分布偏度对预测的影响模式，对于1步预测，有偏性的影响不显著，甚至对称分布的预测效果还要好;对于多步预测，有偏性的影响是显著的。根据我国股市样本，APARCH－SGED设定的预测效果在五个模型中效果最好。

四、结 论

我们考察了在不同分布假定下，APARCH模型的估计与预测，特别是在对称分布中引入偏度系数以刻画样本偏度。通过实证研究，得出分布的有偏性对模型拟合和预测都有显著影响，特别是向前多步预测。这对于刻画金融市场的典型事实、准确进行资产定价、风险度量与管理具有重要意义。

运用芬南德兹—斯蒂尔方法构造偏分布函数优点是计算较为简单，容易估计，同时满足一定条件下各阶矩都存在。一些参数更为复杂的分布，如稳定分布、广义双曲分布能同时刻画分布的尖峰肥尾和偏度，因此是残差时间序列的备选分布，考察它们的拟合效果和预测能力是我们进一步研究的方向。

［1］TAVARES A B，CURTO J D，TAVARES G N.Modeling Heavy tails and Asymmetry using ARCH－type Models with Stable Paretian Distributions［J］.Nonlinear Dynamics，2008，51:231－243.

［2］Schwert W.Stock Volatility and the Crash of S87［J］.Review of Financial Studies，1990，(3):77－102.

［3］GLOSTEN L，JAGANNATHAN R，RUNKLE D.On the Relation between Expected Value and the Volatility of the Nominal Excess Return on stocks［J］.Journal of Finance，1993，48:1779－1801.

［4］HIGGINS M L，BERA A K.A Class of Nonlinear ARCH Models［J］.International Economic Review，1992，33:137－158.

［5］ZAKOIAN J M.Threshold Heteroskedasticity Models［J］.Journal of Economic Dynamics and Control，1994，15:931－955.

［6］GEWEKE J.Modelling of the Persistence of Conditional Variances:A Comment［J］.Econometric Review，1986，5:57－61.

［7］DING Z，GRANGER C W J，ENGLE R F.A Long Memory Property of Stock Market Returns and a New Model［J］.Journal of Empirical Finance，1993，1:83－106.

［8］BOLLERSLEV T.A Conditional Heteroskedastic Time Series Model for Speculative Prices and Rates of Return［J］.Review of Economic Statistics，1987，69:542 －547.

［9］NELSON D.Conditional Heteroskedasticity in Asset Returns:A New Approach［J］.Econometrica，1991，59(2):347－370.

［10］FERNANDEZ C，STEEL M.On Bayesian Modelling of Fat Tails and Skewness［J］.Journal of American Statistical Association，1998，93:359－371.

［11］HARVEY C R，SIDDIQUE A.Autoregressive Conditional Skewness［J］.The Journal of Financial and Quantitative Analysis，1999，34(4):465－487.

［12］HANSEN B E.Autoregressive Conditional Density Estimation［J］.International Economic Review，1994，35(3):705－730.

［13］HARVEY C R，SIDDIQUE A.Conditional skewness in asset pricing tests［J］.Journal of Finance，2000，LV(3):1263－1295.

［14］高见有.不同残差分布下GARCH族模型的分析对比［J］.西部金融，2009，(6):66－67.

［15］李聪.运用GARCH族模型在不同分布下对深证综指的VaR分析［J］.统计与决策.2006，221(9):79－80.

［16］魏宇，高隆昌.基于有偏胖尾分布的随机波动模型估计及其检验［J］.系统管理学报.2008，17(3):266－272.

［责任编辑 张大勇］

Reseach on APARCH Models with Skewed＆ Fat－Tailed Distributions

ZHANG Jia-ping1，2

(1.Research Center of Financial Engineering，South China University of Technology，Guangzhou 510006，China;2 School of Economic，Huaqiao University，Quanzhou 362021，China)

The asymmetry of financial return distribution has been regarded as a "typical fact"，while less attention is relatively paid to the skewness of financial time distribution in the current literature.For the limitation of estimation methodology and computation performance，volatility models assume that the distribution of residuals is normal distribution，or symmetrical fat－tailed distribution，such as t or generalized error distribution.Modeling skewness is much complicated than modeling fat tail.The author constructs the skewed and fat－tailed distributions based on symmetric distributions by using Fernandez－Steel method.And the author studies the prediction of volatility together with APARCH model.Compared with volatility models with symmetrical distribution，empirical results show that there are significant influences of the skewness on simulation and prediction of volatility models.

conditional distribution;APARCH;skewed＆ fat－tailed distribution;time distribution

F830.91

A

1009-1971(2010)02－0078－06

2009－12－26

广东省教育厅项目(08JDTDXM79006)

张家平(1973－)，男，湖北宜昌人，博士研究生，讲师，从事资产定价、风险管理和实证金融研究。