基于实数编码加速遗传投影寻踪方法在物流供应商选择中的应用

杨树果，王新利

(黑龙江八一农垦大学 经济管理学院，黑龙江 大庆 163319)

基于实数编码加速遗传投影寻踪方法在物流供应商选择中的应用

杨树果，王新利

(黑龙江八一农垦大学 经济管理学院，黑龙江 大庆 163319)

针对第三方物流供应商评价指标数据的不确定性和高维性，为克服以往评价方法的不足，提出了综合评价的基于实数编码加速遗传投影寻踪方法。采用投影寻踪模型将高维数据投影到低维子空间上，并对数据结构进行分析;采用基于实数编码的加速遗传算法优化投影方向，克服了投影寻踪模型最佳投影方向难于寻找或容易陷入局部最优的问题;通过最佳投影方向来判断各评价指标对综合评价目标的影响程度和方向，得出投影指标值从大到小的排序。同时，对物流供应商做深入分析，将这一方法用于对低维数据(二级指标)进行评价排序，结果显示与综合评价基本一致，达到了对第三方物流供应商科学、准确的评价，可为企业正确选择物流供应商提供依据。

投影寻踪;第三方物流供应商;加速遗传算法

引 言

随着物流外包的发展，第三方物流以其服务专业化、综合成本低、配送效率高的优势，成为国际物流业发展的趋势和现代物流发展的方向。物流外包也被许多企业视为一项可以集中资源、降低物流成本、增强核心竞争能力的有价值的战略。合理选择第三方物流供应商是许多企业进行物流战略调整过程中必须考虑的问题，而在选择第三方物流供应商中评价指标的选择是否合理，评价方法是否科学，评价结果是否准确，对第三方物流供应商的选择起决定性的作用。

第三方物流供应商选择问题实质是根据多个评价指标及其权重进行综合评判的问题，而综合评判的实质是对高维数据(多个评价指标值)的处理，即降低高维数据的维数。目前，关于第三方物流供应商的选择，特别是在选择和评价方法方面的研究已经引起国内外学者的广泛关注。普遍采用的方法有层次分析法、模糊综合评价法、熵权多目标决策法、BP神经网络、粗糙集等方法［1～7］，这些方法为企业选择物流供应商提供了参考。但层次分析法因受专家的知识和经验的影响，具有一定的人为性;模糊综合评判与综合评分法，由于缺乏系统评价的最优标准，常出现较大误差，甚至得出反常规结论;基于熵的多目标决策法根据评价指标间的变异程度确定各指标权重，在一定程度上消除了人为赋权的缺点，但在实用中常出现各评价指标权重的平均化现象［8］;BP神经网络尽管可以处理高度复杂的非线性模型且具有极高的拟合精度，但在权值的选择上由于采用经验公式，容易陷入局部最优，且易出现“过拟合”现象;粗造集理论对于不确定、不完整的信息具有可测性，但由于该方法考虑的指标因素较少，因而不能准确的反映实际情况。为此，我们采用投影寻踪(Projection Pursuit model，PP)方法，来实现其高维数据的降维过程。

投影寻踪模型自1974年弗里德曼(Friedman J H)和图基(Tukey J W)首先提出以来［9］，被广泛应用各研究领域［10～12］，其基本原理是利用计算机技术，把高维数据通过某种组合投影到低维子空间上，并通过极小化某个投影指标，寻求出能反映高维数据结构或特征的投影，在低维空间上对数据结构进行分析，以达到分析和研究高维数据的目的［9］。该方法能在一定程度上解决了多指标样本分类问题，但是多维数据复杂的空间拓扑结构使得最优投影方向难于寻找［8］。采用传统的优化技术如黄金分割法、爬山法等，容易陷入局部最优，且当优化变量较多时，难以求解。为此，采用基于实数编码的加速遗传算法(Real－ coded Accelerating Genetic Algorithm，RAGA)来优化多维投影方向，实现全局寻优。将遗传算法(Genetic Algorithm，GA)与PP模型结合，通过降低数据维数，将高维数据转化为一维子空间的综合投影指标值，对第三方物流供应商进行评价排序，为企业选择提供依据。

一、评价指标选择及样本数据

1.指标选择

一个完整有效的物流供应商评价指标体系对企业筛选物流供应商非常重要，其评价指标体系的优劣直接影响到物流供应商选取的准确性。由于第三方物流服务供应商与企业是长期的战略伙伴关系，为此企业在选择物流服务供应商时比较关注风险规避、高质量服务获得、服务成本低廉等因素。因此在遵循评价指标选取的代表性、全面性、科学性、实用性、可比性原则的基础上［5］，借鉴现有研究［13］，结合实际情况，从企业实力、服务质量、服务能力、服务成本四个方面构建第三方物流供应商评价指标，如表1所示。

表1 第三方物流供应商评价指标表

2.样本数据

某生产企业考虑将其物流业务外包，拟从六个第三方物流供应商中选择一个最佳合作伙伴为例，根据以上指标对与物流供应商合作过的十家生产企业进行实地和网上调研，针对每一指标对物流供应商进行满意度打分(满分100分)，取平均分，获得数据样本，如表2所示。

表2 第三方物物流供应商评价样本数据

二、第三方物流供应商评价模型构建

依据投影寻踪模型的建模步骤［10］，对第三方物流供应商选择评价建模如下:

1.样本评价指标集的归一化处理

为消除各指标值的量纲和统一各指标值的变化范围，鉴于此研究是要求指标数值越大越好，对于越大越优的指标，采用下面公式进行极值归一化处理，处理结果见表3。

表3 样本数据的归一化处理结果

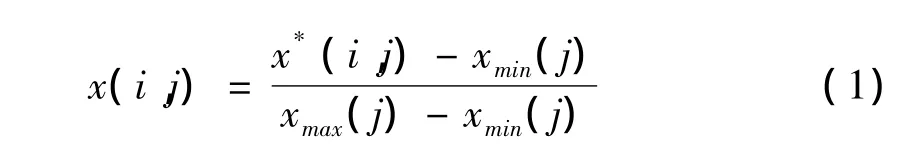
式中，x(i，j)为指标特征值归一化的序列，xmax(j)，xmin(j)分别为第j个指标值的最大值和最小值。

2.构造投影指标函数

根据投影寻踪模型特征，首先将P维数据{x*(i，j)|i=1，2，…，n，j=1，2，…，p}综合成以 a={a(1)，a(2)，…，a(p)}为投影方向的一维投影值，即:

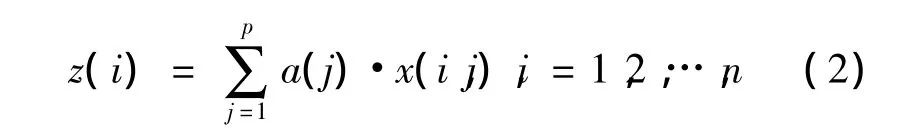
式中:a为单位长度向量。

其次，根据{z(i)|i=1，2，…，n}的一维散布图进行分类与评价。

投影指标函数可以表达成:

式中:Sz为投影值z(i)的标准差

Dz为投影值z(i)的局部密度

式中 E(z)为序列{z(i)|i=1，2，…，n}的平均值，R为局部密度窗口半径，一般按经验选取R=0.1Sz;r(i，j)表示样本之间的距离，r(i，j)=|z(i)－z(j)|;u(t)为一单位阶跃函数，当t≥0时，其值为1，当t≤0时，其值为0。

3.优化投影指标函数

当各指标值的样本集给定时，投影指标函数Q(a)只随着投影方向a的变化而变化。不同的投影方向反映不同的数据结构特征，最佳投影方向就是最大可能暴露高维数据某类特征结构的投影方向。因此可以通过求解投影指标函数最大化问题来估计最佳投影方向，即:

最大化目标函数:Max:Q(a)=Sz·Dz

这是一个以{a(j)|j=1，2，…，p}为优化变量的复杂非线性优化问题，用传统的优化方法处理较难。因此，应用模拟生物优胜劣汰与群体内部染色体信息交换机制的基于实数编码的加速遗传算法(RAGA)来解决其高维全局寻优问题。

遗传算法的基本思想是在初始变化区间内随机生成一组父代个体作为初始解，经过选择、杂交及变异，生成子代个体，通过适应度函数(或目标函数)评价个体的“好坏”，优胜劣汰产生优秀个体，并作为新的父代个体。如此循环迭代，使个体的适应能力不断提高，不断向最优点逼近。加速遗传算法是遗传算法的一种改进算法，它利用在运行过程中产生的优秀个体逐步调整优化变量的初始变化区间，形成加速运行［12］。实践表明，后者的寻优效果强于前者。

将PP模型中的投影指标函数Q(a)作为目标函数，各个指标的投影a(j)作为优化变量，运行RAGA的八个步骤［11］，即可求得最佳投影方向a*(j)及相应的投影值z(i)，将z(i)按其值大小进行比较，从而求得评价结果。

4.分类或评价

把由上一步求得的最佳投影方向a*代入公式(2)中可得各样本点的投影值z*(i)。将z*(i)与z*(j)进行比较，二者越接近，表示样本i与j越倾向于分为同一类。若按z*(i)的值从大到小排序，则可以将对物流供应商的评价从优到劣进行排序。

(1)综合指标评价

采用Matlab7.0编程处理，建立第三方物流供应商评价标准的数学模型。选定父代初始种群规模为n=400，交叉概率pc=0.80，变异概率pm=0.80，优秀个体数目选定为20个，α=0.05，加速次数为20，得出最大投影指标值为0.3170，各个状态变量的最佳投影方向:

a*= (0.0086，0.2217，0.2826，0.3419，0.5491，0.2522，0.1713，0.2313，0.4636，0.0750，0.0636，0.2650，0.1009，0.0336)

将a*代入公式(2)，即得各供应商综合评价的投影值:EMBED Equation.3。

将EMBED Equation.3从大到小排列，得到各物流供应商的综合排名，即Ⅴ>Ⅵ>Ⅲ>Ⅰ>Ⅳ>Ⅱ，由此可见，供应商5的综合评价最好，供应商6次之，再次是供应商3、供应商1和供应商4，最差的是供应商2。

(2)分项指标评价

为确保评价的一致性，采用以上方法，对其二级指标进行评价(具体评价指标数分别为5、4、3、2个)，以便对六家供应商作更深入分析。这里需要说明的是投影寻踪方法适合于多个评价指标值的处理，但并不排除其对低维数据的适用性。采用Matlab7.0编程处理，计算结果如下:

企业实力评价:最大投影指标值为0.3013，各个变量的最佳投影方向 a*=(0.0233，0.0918，0.3690，0.6000，0.7035)，各供应商企业实力的投影值 z*(j)=(1.0208，0.0998，1.3868，1.0058，1.0230，1.6743)。得供应商企业实力排名:Ⅵ>Ⅲ>Ⅴ>Ⅰ>Ⅳ>Ⅱ，即供应商6的企业实力最强，其次是供应商3，再次是供应商5、供应商1、供应商4，最弱的是供应商2。

服务质量评价:最大投影指标值为0.3834，各个变量的最佳投影方向 a*=(0.6821，0.1065，0.5843)，各供应商服务质量的投影值z*(j)=(0.747，0.0426，1.6905，0.7367，1.4220，0.7478)。得供应商服务质量排名:Ⅲ>Ⅴ>Ⅵ>Ⅰ>Ⅳ>Ⅱ，即供应商3的服务质量最好，其次是供应商5，再次是供应商6、供应商1、供应商4，最差的是供应商2。

服务能力评价:最大投影指标值为0.2662，各个变量的最佳投影方向 a*=(0.6440，0.4352，0.6292)，各供应商服务质量的投影值z*(j)=(1.5224，0.9926，0，0.8236，1.5219，0.6823)。得供应商服务能力排名:Ⅰ>Ⅴ>Ⅱ>Ⅳ>Ⅵ>Ⅲ，即供应商1的服务能力最强，其次是供应商5，再次是供应商2、供应商4、供应商6，最弱的是供应商3。

服务成本评价:最大投影指标值为0.1997，各个变量的最佳投影方向 a*=(0.2237，0.9747)，各供应商服务质量的投影值z*(j)=(0.5575，1.1984，0.1398，0.1392，1.0312，1.0592)。得供应商服务成本排名:Ⅱ>Ⅵ>Ⅴ>Ⅰ>Ⅲ>Ⅳ，即供应商2的服务成本最低，其次是供应商6，再次是供应商5、供应商1、供应商3，服务成本最高的是供应商4。

(3)结果分析

将各供应商的综合评价及分项评价进行汇总，如表4所示。

表4 第三方供应商综合评价与分项评价排名

根据表4的排名，从综合评价角度看，企业在选择第三方物流供应商合作伙伴时，可考虑供应商5。因为该供应商在综合评价中位于首位，且分项排名(二级指标评价)虽不是最优(分别处在第3、2、2、3 位)，但没有弱项，总体上能够满足企业物流外包的要求，适合建立长期合作关系。但与此物流供应商协作时需要高度关注它的服务能力，以免由此延长产品供应的时间;其他供应商虽在不同指标评价中优势明显，但劣势也很突出。如供应商2服务成本最低，但整体实力最弱，服务质量最差，虽然与该供应商合作可明显降低物流成本，但长期看，不利于企业物流外包业务的开展。

从综合评价的最佳投影方向可以看出，影响程度较大的指标依次是:社会声誉、增值服务、发展潜力、管理水平、快速响应能力、准时交货率、订单履行准确率等;从二级指标的最佳投影方向发现，各指标影响基本与综合评价一致，如企业实力评价中，影响程度大的指标依次是社会声誉、发展潜力、管理水平等。

物流供应商实力的强弱，反映了企业与其长期合作是否稳定，服务能力的强弱和服务质量的优劣，决定了总体的服务效率和水平。虽然服务成本是任何一家企业都必须考虑的问题，但从物流的角度看，它绝不应该是首要因素，因为物流更讲求的是服务效率与质量。

结 论

通过以上实例分析可知在进行第三方物流供应商的选择评价时，采用基于实数编码的加速遗传算法的投影寻踪模型是可行的，且较其他方法显现出无可比拟的优势，为企业选择第三方物流供应商提供了一种新的研究方法。通过研究可得出以下结论:一是利用投影寻踪模型对数据处理的高维降维技术，可对具有模糊性、不确定性的高维数据进行综合评判、排序，且效果很好。二是采用基于实数编码的加速遗传算法来优化投影方向，克服了投影寻踪模型最佳投影方向难于寻找或容易陷入局部最优的问题。三是最佳投影方向可以科学的反映各评价指标的重要程度，使得评价结果客观、准确。采用基于加速遗传算法的投影寻踪模型对二级指标(指标数量较少)评价的结果与综合评价基本一致，且与实际经验基本相符，但理论上是否确实有效，还有待进一步验证。

［1］童明荣，薛恒新，林琳.现代第三方物流供应商的选择［J］.大连海事大学学报，2006，(11):14－18.

［2］柳键.物流供应商的评价与选择研究［J］.工业技术经济，2007，(1):95 －96，98.

［3］李思志，叶柏青.基于集对分析的第三方物流供应商选择模型［J］.物流科技，2005，(4):31－35.

［4］方承武，雷勋平.模糊决策法在物流供应商选择中的应用［J］.安徽工业大学学报:社会科学版，2005，(1):46－47.

［5］董景峰，王刚，吕民，高国安.基于熵的第三方物流供应商选择评估模型［J］.计算机工程与应用，2007，(43):194－196.

［6］俞兆城，赵永刚，朱建坤.基于BP神经网络物流供应商能力评估研究［J］.中国管理信息化，2008，(5):86－88.

［7］黄颖，李芳芳.基于粗集理论的物流供应商选择研究［J］.江苏科技大学学报:自然科学版，2008，(12):67－71.

［8］MONTANARI A，LIZZANI L A Projection Pursuit Approach to Variable Selection［J］.Computational Statistics＆ Data Analysis，2001，35:463－473.

［9］FRIEDMAN J H，TUKEY J W.A Projection Pursuit Algorithm for Ex － ploratory Data Analysis［J］.IEEE.Trans.Compute，1974，23:881 －889.

［10］付强，付红，王立坤.基于加速遗传算法的投影寻踪模型在水质评价中的应用研究［J］.地理科学，2003，(4):236 －239.

［11］关法春，梁正伟.基于遗传算法的投影寻踪模型对小花碱茅最佳收获期的判定［J］.农业系统科学与综合研究，2009，(8):336－339.

［12］付强.数据处理方法及其农业应用［M］.北京:科学出版社，2006:297－306.

［13］魏世奇，蔡临宁.第三方物流供应商选择和评价指标体系的研究［J］.商场现代化，2007，(2):127－128.

［责任编辑 张大勇］

Application of PP Model Based on RAGA in the Selection of Logistics Provider

YANG Shu-guo，WANG Xin-li

(College of Economics ＆ Management，Heilongjiang August 1＇st Land Reclamation University，Daqing 163319，China)

In order to overcome the lack of previous evaluation methods，we suggest Projection Pursuit method based on Real－coded Accelerating Genetic Algorithm for the uncertain and high－dimensional nature of the evaluation indicator data of TPL providers.Projecting the high－dimensional data onto the low－dimensional sub－space by PP model and then analyzing the data structure，optimizing the projection direction by using RAGA to overcome the difficulty of finding the best projection direction or the problem of falling into local optimum，the paper determines the extent of impacting and the direction of the evaluation indicators on comprehensive evaluation target and calculates the sort of the projection index value in descending order.Furthermore，we try to use this method on low －dimensional data to analyze logistics providers deeply and the results show that basically consistent with the comprehensive evaluation.We achieve scientific and accurate evaluation to TPL providers and can provide a basis for the enterprise to select a logistics provider.

projection pursuit;TPL provider;RAGA

C934

A

1009-1971(2010)02－0089－06

2010－02－17

国家自然科学基金(70672117)

杨树果(1977－)，女，黑龙江五常人，讲师，从事企业管理研究;王新利(1956－)，男，山东五莲人，管理学博士，教授，博士生导师，从事农产品流通与农村物流研究。