基于正则神经网络模型的时滞混沌系统预测控制

李冬梅,陈军霞

(河北科技大学经济管理学院,河北石家庄 050018)

基于正则神经网络模型的时滞混沌系统预测控制

李冬梅,陈军霞

(河北科技大学经济管理学院,河北石家庄 050018)

研究模型未知、不稳定的不动点位置及其局部性态未知情形下的时滞混沌系统的控制问题。提出了一种神经网络预测控制方法,将模型未知时的时滞混沌运动控制到不稳定的不动点处。分析了控制系统(包括观测器、正则神经网络预测器和在线训练的线性神经网络预测控制器)的稳定性,与现有同类方法比较,本方法收敛速度快,算法简便。仿真实验表明了本方法的有效性。

时滞混沌系统;混沌系统控制;神经网络预测控制;正则神经网络

混沌是自然界与人类社会普遍存在的运动形态,近年来,混沌系统的控制研究得到人们越来越多的关注[1-3]。OGY法通过小参数扰动将混沌运动稳定在嵌入于混沌吸引子中的不稳定周期轨道(UPO)上,针对OGY法,人们进行了多种改进并应用于各种不同的混沌系统。由于OGY法需要已知UPO的位置及其局部线性性态,因而必须事先确定UPO的位置及其局部性态。当混沌系统的数学模型未知时,则必须估计UPO的位置及其局部性态,常导致控制效果不够理想。

研究表明,即使是结构简单的非线性系统也可能产生复杂的混沌行为。将时滞项引入一阶系统便可以引起复杂的混沌运动,其原因是时滞项增加了系统的复杂性并使系统变成了无穷维。目前已发现许多系统包含时滞项。与大量的研究文章关注无时滞混沌系统相比,只有极少的研究涉及到时滞混沌系统的控制,其中BABLOYAN TS和CEL KA应用Pyragas法对混沌系统进行了研究[4-5],TIAN等提出了一种参考模型自适应控制方法来控制连续型时滞混沌系统[6],文献[7]研究了一类时滞混沌系统的时滞依赖最优保性能控制问题,文献[8]研究了一类时滞混沌系统的反馈控制同步问题,文献[9]提出了一种神经网络控制策略,用于将模型未知的时滞混沌系统控制到不稳定的不动点(UFP)处,但该方法需要很长的控制时间,神经网络控制器的训练迭代次数多。

与常规混沌系统相比,由于时滞混沌系统的复杂性,使得对时滞混沌系统的控制难度更大,所需控制时间更长。为了更好更快地控制时滞混沌系统,有必要应用预测控制方法,并且采用预测性能更强的预测模型。预测控制方法包括模型预测、滚动优化和误差反馈校正等环节,既具有预测、优化功能,又利用了实时反馈信息,因此,它对被控系统有较强的控制能力。笔者将预测控制的思想引入时滞混沌系统的控制中,提出了一种基于预测控制的神经网络控制方法,将模型未知时的混沌运动控制到不稳定的不动点(UFP)处。所提出的控制系统包括观测器、正则神经网络预测器和在线训练的线性神经网络预测控制器(LNPC)。本控制系统不需要UFP的位置及其局部性态等知识,因而能够有效地解决模型未知、不动点位置及其局部性态未知情形下的时滞混沌系统的控制问题。与其他现有同类方法比较,本方法有更快速的响应性能,需要较短的控制时间就能实现时滞混沌系统的稳定,神经网络控制器的训练迭代次数少,控制系统的稳定性和神经网络预测控制器的收敛性能够得到保证。

1 问题的描述

考虑如下时滞混沌系统:

加入控制项后,被控时滞混沌系统为

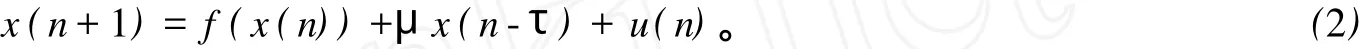
其中:x(n)∈R是n时刻的状态变量,假定它们是可观的;u(n)∈R是n时刻的控制信号;非线性映射f:R→R是未知的;μ是未知参数;时滞项τ>0也是未知的,但其上限v是已知的(τ≤v)。无控制信号时的系统(1)表现出混沌行为,系统(1)的不稳定不动点xf满足:xf=f(xf)+μxf。

本文讨论只有一个不动点xf被嵌入到混沌吸引子中的情形,目标是使混沌运动被稳定在时滞混沌系统的不稳定不动点处。

2 控制系统

2.1 控制方法

2.1.1 观测器

观测器的工作情形如下:

1)利用时滞项对系统状态进行重构,T

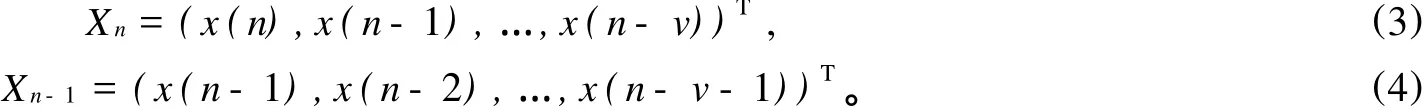
2)估计重构状态之间的距离。

3)当此距离小于一个小阈值ε,即

时观测器起作用,LNPC传递一个控制信号到混沌系统,然后对LNPC进行训练。当式(5)不满足时,控制信号为零,LNPC不进行训练。

当ε是一个小正数时,若式(5)成立,则表明混沌轨道落入了xf的小邻域内,观测器限定了控制器的工作,只有当重构轨道Xn落入Xf=(xfxf…xf)T的小邻域内,控制器才传递一个控制信号到混沌系统,然后按学习规则对控制器进行训练。

2.1.2 线性神经网络预测控制器(LNPC)的输出

经过重构之后,混沌系统(1)变为

其中非线性映射F:Rv+1→Rv+1是光滑函数。式(6)实际上是一个方程组,而其中的第1个方程:

与式(1)是等价的。加入控制项后,被控时滞混沌系统为

其中F1是F的第1行。

令x(nk)为训练时刻k时满足条件(5)的混沌轨道(k≤nk),其中nk为训练时刻k时混沌系统的迭代次数,LNPC的输出为

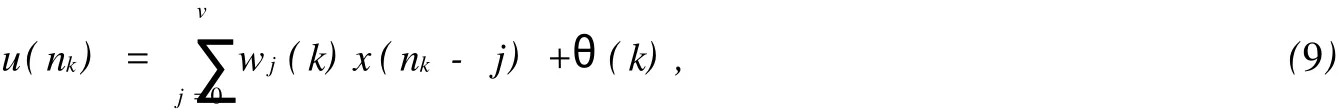
其中k为LNPC的训练次数(即观测器起作用的次数),wj(k)是输入层第j个神经元到输出层神经元的连接权值,θ(k)为输出层神经元的偏置项,它们的值按δ规则更新。

其中:η是学习率,E(k)是误差函数,经上述公式迭代来更新权值可以降低误差E(k)。

2.1.3 正则神经网络预测器

在神经网络的研究中,一个重要的问题是神经网络的泛化性能,即对于其训练集之外的样本是否能作出正确的反应。对于大多数的学习问题,能够获取的学习样本毕竟是有限的,而且还可能包括一些模糊的、甚至是带有一定误导性信息的样本。如果神经网络只是记忆训练集中的样本,那么,对于新的样本,其反应可能是错误的。导致前向网络泛化性能差的重要原因是过拟合,一种有效地限制网络过拟合的方法是正则化方法,即在目标函数中加入正则项。正则神经网络极大地提高了网络的泛化能力,因而也改善了神经网络模型的预测性能,笔者在对未知的被控混沌系统进行辨识、预测时,采用了正则神经网络。

事先用神经网络对未加控制项的混沌系统进行辨识,然后在控制系统工作时在线训练这个神经网络辨识器。设用神经网络(此处用正则神经网络)辨识出的对应系统(7)的模型为G,则系统的模型输出为

nk+2时刻的模型输出为

这里nk+2时刻的模型输出的值是在nk时刻预测出的,u(nk+1)可仍取u(nk)。

考虑到模型有误差,引入偏差项x(nk+1)-^x(nk+1),得系统预测输出^xp(nk+2):

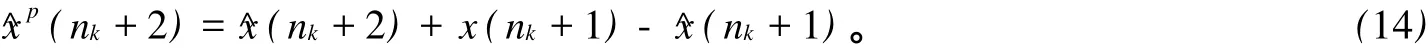
2.1.4 线性神经网络预测控制器的目标函数

控制器的目标函数(亦即训练控制器的误差函数)为E(k)。 ΓC,ΓU为权系数。其中:

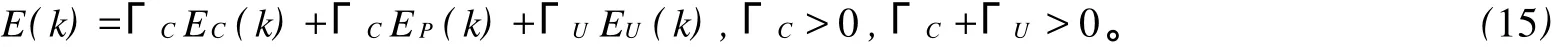
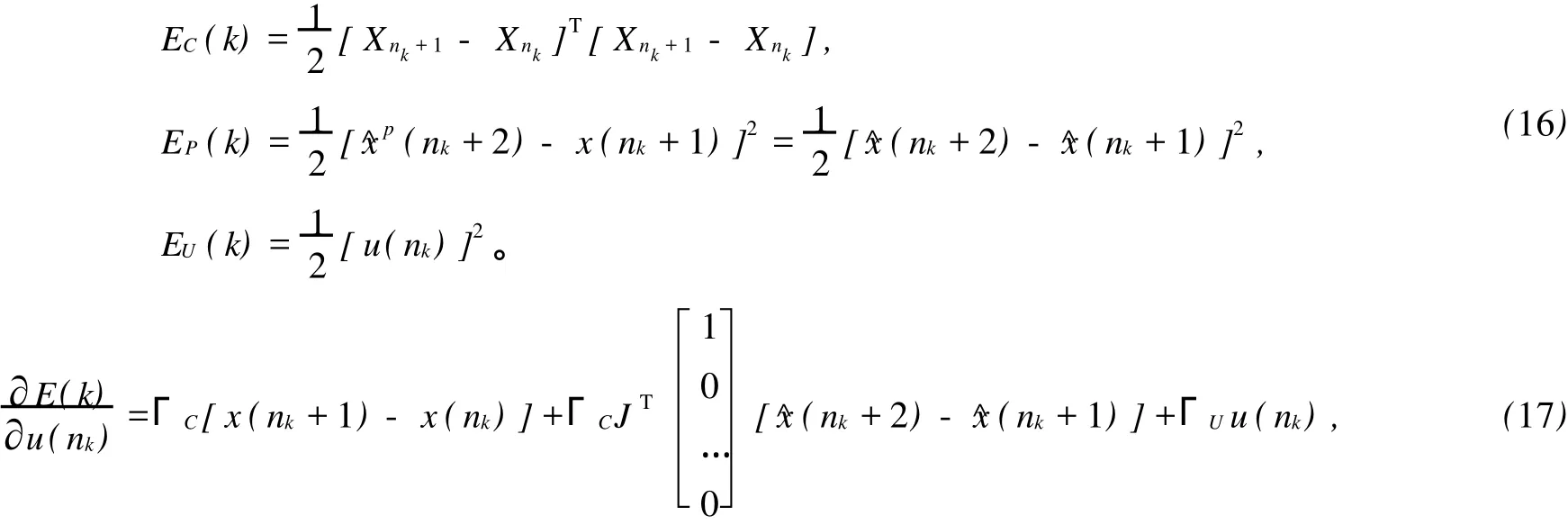
2.2 步骤

控制系统的工作步骤如下:

1)混沌系统按式(1)迭代1步;

2)如果重构轨道Xn和Xn-1满足式(5)条件,则转入步骤3),否则转入步骤7);

3)按式(9)送1个控制信号U(nk),混沌系统按式(2)再迭代1次;

4)按式(12)和式(13)求nk+1,nk+2时刻的预测值^x(nk+1),^x(nk+2);

5)按式(10)、式(11)和式(17)在线训练1步控制器;

6)训练1步辨识器(输入为Xnk,期望输出为x(nk+1)-u(nk)),n←nk+1,回到步骤2);

7)混沌系统按式(1)迭代1步;

8)训练1步辨识器(输入为Xn,期望输出为x(n+1)),令n←n+1,回到步骤2);

上述步骤重复进行,混沌轨道将被稳定在期望的UFP上。

3 稳定性分析

对于式(6),可以加上1个控制项,变为

可以看出,式(18)的第1个方程就是本文讨论的情况。通过重构系统状态,时滞混沌系统可以转化为非时滞混沌系统,因此,可以得到控制系统的稳定性条件为

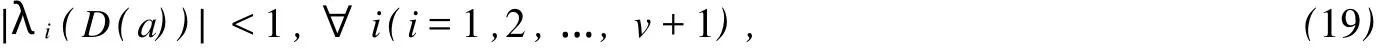
其中λi(D(a))为D(a)的第i个特征值。

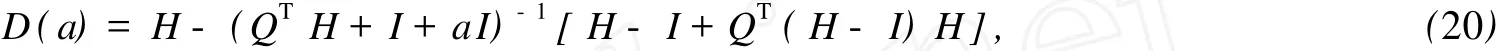
可以通过调节a的取值,保证|λi(D(a))|<1,从而能够保证控制系统的稳定性。

4 仿真实验

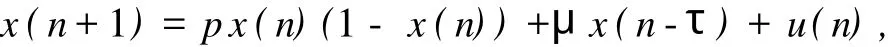
用如下时滞混沌系统进行仿真实验来检验笔者提出的控制方法。其中p=3.5,μ=0.08,τ=1,并假定已知v=3。不加控制项时,嵌入在混沌吸引子中的不动点为xf= 0.737 1。通过调节a的取值,保证控制系统的稳定性。由H和J的定义知,J≈H,将H值代入到式(20)中,求得满足稳定性条件的a值范围,a∈[0.000 1,11.35],说明对于较大范围的a值,控制系统都能保证其稳定性。取控制系统的参数为a=6.5(ΓC= 1,ΓU=6.5),η=0.01,观测器阈值为ε=0.32。LNPC的初始权值Wij(0)和θi(0)取为[-0.01, 0.01]间的均匀分布随机数。图1示出了仿真实例的控制结果,可以看出对时滞混沌系统的控制取得了很好的效果,而且需要的控制时间较短,迭代和训练的次数较少。当迭代次数n= 15 000,训练次数k=3 816时,混沌系统被稳定在不动点处,而采用现有方法(文献[9]中的方法),需要的迭代次数多达66 000次。

这里,迭代次数n事实上即为混沌系统的采样次数,n值越小,则用于稳定时滞混沌系统所需的时间越短。仿真实验表明,笔者提出的控制系统能够比现有同类方法更快地将混沌运动稳定到系统的不稳定不动点处(按本文所作的仿真实验来看,本文的方法比现有方法快3.4倍)。

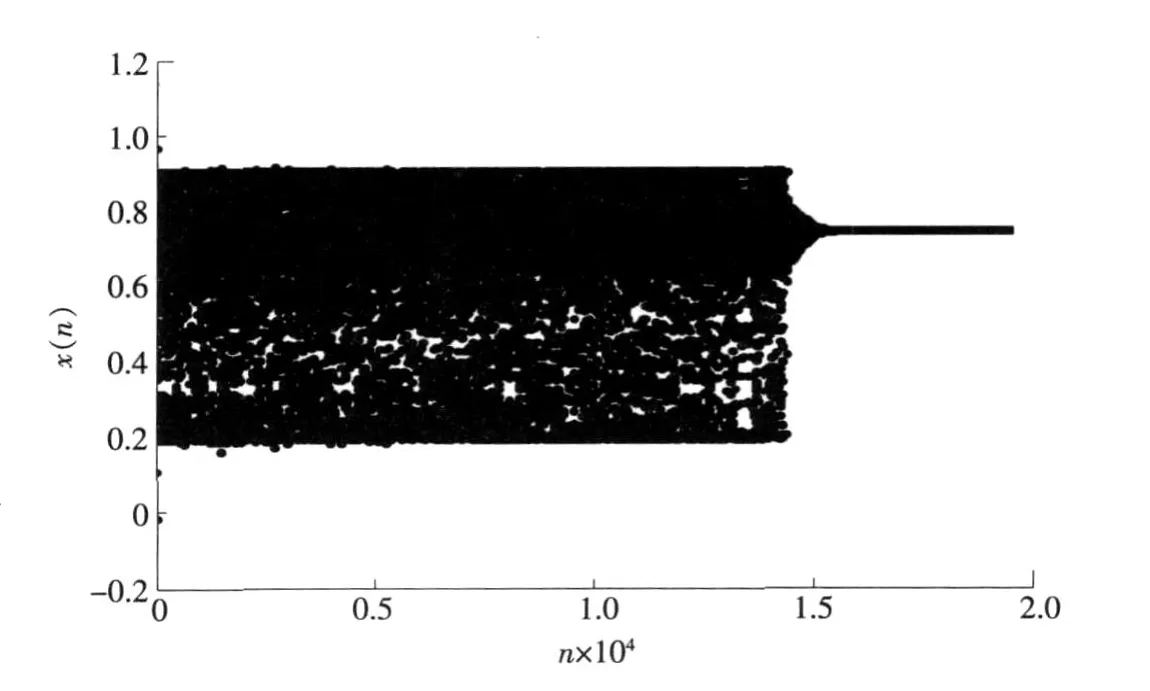
图1 时滞混沌系统的控制结果Fig.1 Control result of the chaotic system

5 结 语

提出了一种基于正则神经网络模型的预测控制方法,将模型未知时的时滞混沌系统稳定到它的一个不稳定不动点(UFP)处。此控制系统不需要UFP的位置及其局部性态等知识。与其他同类方法比较,本方法需要的控制时间较短,训练迭代次数较少,而且算法简便。一般情况下,通过调节a值能保证控制系统的稳定性。理论分析和仿真实验都表明,本文提出的控制系统能有效地解决模型未知、不动点位置及其局部性态未知情形下的时滞混沌系统的控制问题。

[1] 王 森,蔡 理,吴 刚.量子细胞神经网络超混沌系统的追踪控制与同步[J].控制与决策(Control and Decision),2008,23(2):204-207.

[2] 赵 琰,张化光.一类参数不确定性混沌系统的T-S模糊控制[J].系统仿真学报(Journal of System Simulation),2008,20(12):3 134-3 137.

[3] 马国进,齐冬莲.基于状态观测器的混沌动态系统跟踪控制[J].电路与系统学报(Journal of Circuits and Systems),2009,14(2):27-31.

[4] BABLOYANTSA,LOURENCO C,SEPULCHREJ A.Controlof chaos in delay differential equations,in a network of oscillatorsand in model cortex[J].Physica D,1995,86:274-283.

[5] CELKA P.Delay differential equations versus 1D-map:Application to chaos control[J].Physica D,1997,104:127-147.

[6] TIAN Yu-chu,GAO Fu-rong.Adaptive control of chaotic continuous-time systems with delay[J].Physica D,1998,117:1-12.

[7] 罗晓琴,张文安,俞 立.时滞混沌系统的时滞依赖最优保性能控制[J].浙江工业大学学报(Journal of Zhejiang University of Technology),2008,36(1):52-56.

[8] 谢英慧,张化光,王福山.一类参数不确定时滞混沌系统的反馈控制同步[J].东北大学学报(自然科学版)(Journal of Northeastern University(Natural Science)),2008,29(5):613-616.

[9] KON ISH I K,KOKAM E H.Learning control of time-delay chaotic systems and its applications[J].Int J Bifurcation and Chaos,1998, 8(12):2 457-2 465.

Predictive control of time-delay chaotic system s based on regularized neural network model

L IDong-mei,CHEN Jun-xia
(College of Economical and Management,Hebei University of Science and Technology,Shijiazhuang Hebei 050018,China)

The control of the time-delay chaotic system is studied w hen the system model,the location of the unstable fixed point and the local dynamics at the point are unknow n.A neural p redictive control method is p roposed to control the chao tic motion in an unknow n time-delay chaotic system onto the unstable fixed point.The p roposed control system includes a watcher,a regularized neural p redicto r and an on-line trained linear neural p redictive controller.We analyze the stability of the control system.The p roposed algo rithm is simple and its convergence speed is higher than that of existing similar algorithm.The simulations demonstrate the effectiveness of the controlmethod.

time-delay chaotic systems;control of chaotic system s;neural p redictive control;regularized neural netwo rk

TP13

A

1008-1542(2010)05-0442-05

2010-03-03;

2010-05-28;责任编辑:张 军

李冬梅(1963-),女,河北香河人,教授,博士,主要从事系统工程理论与应用、信息管理方面的研究。