星载SAR成像处理系统中多线程矩阵转置的设计和实现

田 蕾 范士明

(航天恒星科技有限公司,北京 100086)

1 引言

矩阵转置被广泛地应用于图像处理、信号处理和统计学等领域,在合成孔径雷达(SAR)的成像处理系统中也有非常重要的应用。在进行SAR 的成像处理时,数据一般是以矩阵形式排列的,可以定义距离向采样为行方向,方位向采样为列方向。成像处理是对矩阵中的按行或按列的数据进行多次一维或二维的联合处理。在要求快速成像处理时,通常都是将二维联合处理转化为一维处理的算法,即在进行完行(列)处理后,还需要针对列(行)进行处理。在行、列处理的转换中,需要频繁多次进行矩阵转置操作。矩阵转置算法的时效性决定了整个成像系统处理速度是否能够满足应用需求。因此,有必要对矩阵转置算法进行分析和研究。

随着计算机技术的不断发展,多核处理器已经成为各种处理平台的基本配置。由于本论文的研究环境是共享内存的并行机,研究的矩阵转置算法必须能够适用于这种系统。现有的矩阵转置算法一般都是串行的,无法充分利用多核处理器。多线程是基于这种硬件系统的并行处理技术,因此,有必要对多线程的矩阵转置算法进行研究。

本文主要对多线程技术在星载SAR 地面成像处理系统中的应用进行研究。第2部分介绍SAR的成像处理系统;第3部分研究和分析矩阵转置方法;第4部分研究和分析多线程矩阵转置的并行处理方法;第5部分研究和分析多线程矩阵转置的实验结果及结论。

2 SAR 的地面成像处理系统

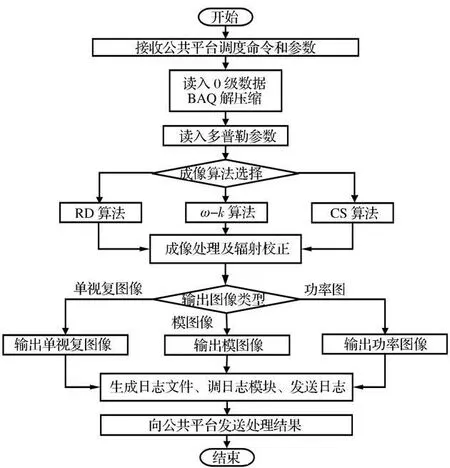
图1 星载SAR 的地面成像处理系统Fig.1 Image processing system of spaceborne SAR

星载SAR 的地面成像处理系统主要完成原始回波数据的分块自适应量化(BAQ)解压缩和聚焦成像处理并进行辐射校正。生成的数据可以通过公共平台提供产品生成模块,生产指定格式的1级产品,或通过几何校正等进一步的处理,实现更高级别的产品生产。本论文主要对条带模式SAR 的成像处理进行研究和讨论,因此,假设此地面成像处理系统主要处理条带模式SAR 的原始回波数据。此星载SAR 的地面处理系统的处理流程如图1所示。

如图1所示,成像处理可以根据需要在一定范围内选择适合的成像算法,为进一步说明矩阵转置的作用,详细分析距离-多普勒(Range Doppler,RD)和CS(Chirp Scaling)成像算法的处理流程,如图2、3所示。

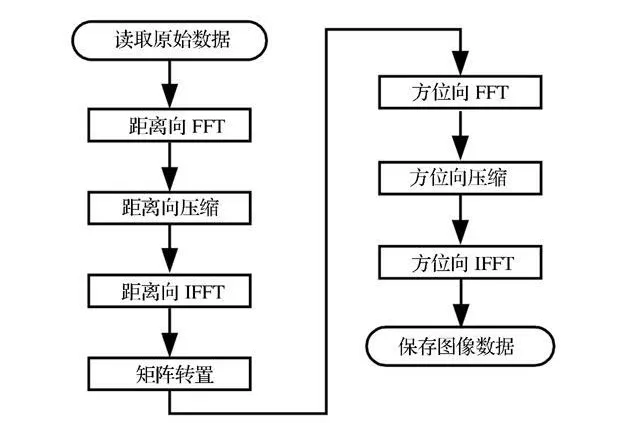
图2 RD算法的处理流程Fig.2 Processing procedures of RD algorithm

图3 CS算法的处理流程Fig.3 Processing procedures of CS algorithm

3 矩阵转置

从以上两种算法的处理流程可以看出,矩阵转置是SAR成像处理中必不可少的一个处理步骤。如果没有专门的转置存储设备的成像处理系统,可以用两种方式进行存储:一种是处理器内部的存储器足够大,可以将所有需要的数据全部读入内部存储器中进行转置;另一种是处理器内部的存储器不够大,不能将所有待处理的数据一次全部读入,一般通过内存和外存共同完成转置处理。随着存储器价格的不断降低,现阶段的内存大小一般能够满足一次把所有需要的数据全部读入的条件,因此,本文只对内存的矩阵转置算法进行研究和分析[1-2]。

3.1 方阵转置

本论文的开发环境是Linux 和C++,矩阵数据被存储在动态分配的内存里,按照行或列的顺序存储在动态数组里,矩阵转置也是在数组内完成的。方阵转置相对于矩阵转置更容易被实现,为了使问题简化,先分析方阵转置的处理方法。令方阵A=(aij)(n+1)×(n+1),i,j =0,…,n,i =j,n =2N-1,N ≥0 且N ∈Z,转置后AT=(aji)(n+1)×(n+1),假设A按行存储成一维动态数组,则转置后的AT按列存储成一维动态数组,buff 1是存储A和AT的内存空间,buff 2是存储中间结果的内存空间。下面介绍两种主要的方阵转置方法:直接法和递归法。

3.1.1 直接法

根据方阵存储链表的特点,直接转置只需要把每对aij 和a ji 直接互换就可以实现。这种方法原理比较简单,易于实现,只在原来的内存上就可以进行处理,但处理较大矩阵的效率不是很高,速度较慢。具体的处理过程如图4所示。

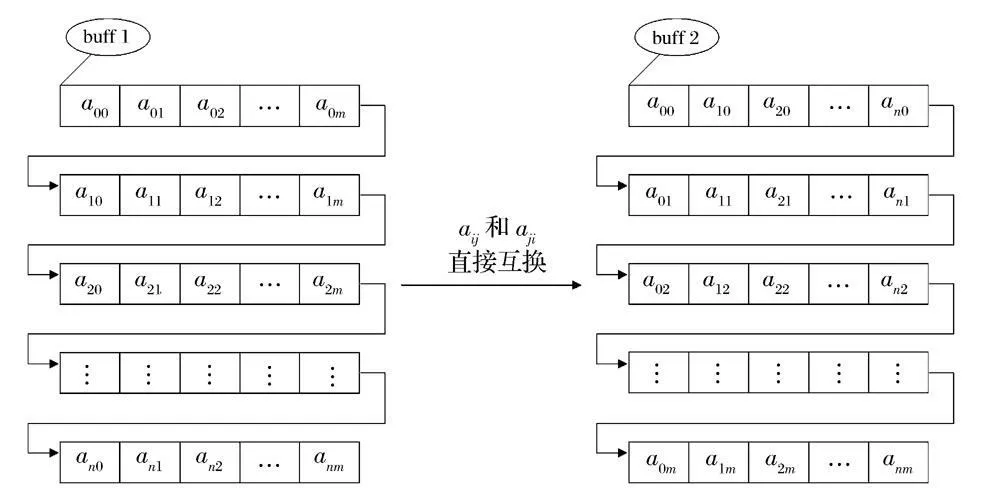
图4 方阵转置直接法的处理过程Fig.4 Process of square matrix transposition direct method

3.1.2 递归法

对于较大的方阵可以用直接算法进行转置,但效率并不是很高,速度有待提高,提出递归法进行转置。递归法的原理相对要复杂一些,对递归的划分和返回要特别注意。具体的实现过程如以下三步所示。

第二步,多次四等分后得到小方阵,对这些小方阵用直接法实现各个小方阵的转置;

第三步,递归的返回过程,依次完成各次递归划分后逆对角线上小方阵的互换,直到第一次递归划分得到4个小方阵,把逆对角线上的小方阵互换,实现整个大方阵的转置。

具体的递归法的处理过程如图5所示。

可以看到,以上两种方阵转置方法不用额外申请大块连续的内存,整个转置的实现都是在原来的内存上完成的,有效地节省了内存空间。

图5 方阵转置递归法的处理过程Fig.5 Process of square matrix transposition recursive method

3.2 矩阵转置

令A=(aij)(n+1)×(m+1),i =0,…,n,j =0,…,m,n =2N-1,m =2M-1,N ≥0 且N ∈Z,M ≥0 且M ∈Z,转置后AT=(aji)(m+1)×(n+1),假设A按行存储成链表,则转置后的AT按列存储成链表。由于矩阵不具有方阵行列相等的特点,不能用方阵转置的直接法和递归法实现转置,需要另外申请一大块连续的内存空间存放中间结果,具体的实现过程如以下三步所示。

第二步,把buff 2 中对应的小方阵分别在各自的存储区内进行转置,当t ≤2α时,用方阵直接转置法,当t ＞2α时,用方阵递归转置法;

第三步,把已转置的小方阵从buff 2 对应的存储区中取出,存放到buff 1 对应的存储区中,完成整个大矩阵的转置。

具体矩阵转置的处理过程如图6所示。

4 多线程的矩阵转置

所谓多线程就是将应用程序划分成一个或多个同时运行的任务。在这种共享内存的系统上进行并行处理的关键是对多处理器共享内存的访问控制,其基本实现模式有共享全部数据结构(Shared Everything)与共享局部数据结构(Shared S omething)两种。两种都允许处理器通过存/取共享内存来进行通信,其主要区别在于共享全部数据结构将所有的数据结构都放在内存,而共享局部数据结构需要用户显式地指定出哪些数据结构是潜在共享的,哪些是仅有某处理器私有的。由于本论文是对一帧原始回波数据的成像处理中矩阵转置的多线程处理方法进行研究,所以重点关注共享全部数据结构的实现模式[3-4]。

4.1 共享全部数据结构

这种模式的好处在于用户可以很容易地利用一个已经编写好的串行程序,并将其转化为一个共享内存的并行程序,因为用户不需要事先区分哪些数据是需要被其他处理器访问的。但是,这种模式存在任何单个处理器对内存的访问都有可能影响到其他处理器的处理结果的问题。因此,对内存的访问要特别关注同步和互斥的问题[5-8]。

Linux系统对共享全局数据结构是通过线程机制实现的,即提供线程库支持并行处理。可移植操作系统接口线程库(POSIX th read,Pthread)是一套通用的线程库,它广泛地被各种Unix所支持,是由可移动操作系统接口(Portable Operating System Interface,POSIX)提出的,具有良好的可移植性。使用Linux Pthread 的基本步骤如下:

第一步,以单进程的方式开始程序的执行;

第二步,初始化所需的各个锁;第三步,调用pthread_create 函数创建新线程;第四步,并行执行线程代码,正确加锁和解锁,以保证处理器对内存访问的正确性。

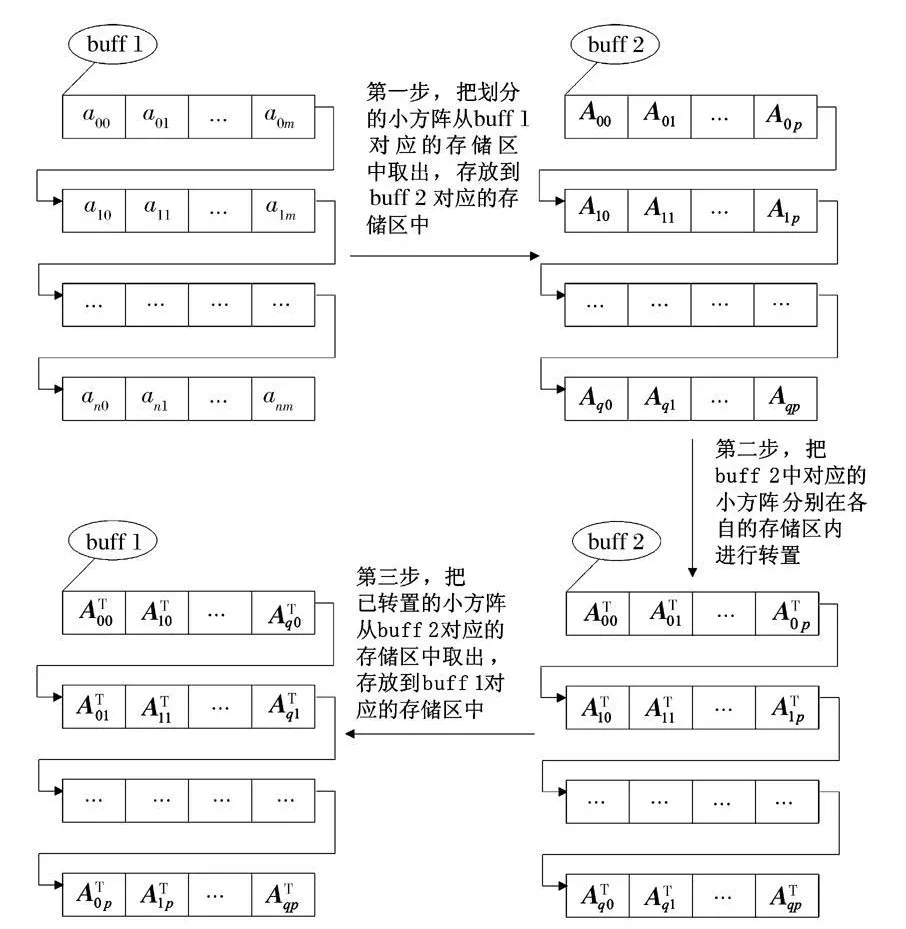
图6 矩阵转置的处理过程Fig.6 Process of matrix t ransposition

4.2 多线程矩阵转置的并行处理方法

第一步,线程1 和线程2分别把buff 1 中的大矩阵划分成若干个小方阵,A=(Aij)(q+1)×(p+1) =

根据一帧原始回波数据的特点,创建的线程数Nthread=2N,N ≥0 且N ∈Z ,为了简化分析的过程,令N =1 ,则Nthread=2。具体的实现过程如下三步所示。其中i =0,…,q,j =0,…,p,(q+1)*t =(n+1),(p+1)*t =(m+1),t(令t =2α,α≥0 且α∈Z)为小方阵的大小,线程1 和线程2分别把划分的小方阵从buff 1 对应的存储区中取出,存放到buff 2 对应的存储区中;

第二步,线程1 和线程2分别把buff 2 中对应的小方阵分别在各自的存储区内进行转置,当t ≤2α时,用方阵直接转置法,当t ＞2α时,用方阵递归转置法;

第三步,线程1 和线程2分别把已转置的小方阵从buff 2 对应的存储区中取出,存放到buff 1 对应的存储区中,完成整个大矩阵的转置。

具体多线程转置的并行处理过程如图7所示。

以上是为了对问题的模型进行简化,对两个线程矩阵转置的并行处理方法进行的研究和分析,实际处理时可以根据需要创建线程数,但根据一帧原始回波数据的特点,必须满足Nthread=2N,N ≥0 且N ∈Z。

5 实验和结论

5.1 在HP 服务器上的实验结果

实验所用的平台为HP Proliant DL580,是一台通用服务器。

本文所研究的多线程矩阵转置在HP 上的运算结果如表1所示。由于这台服务器具有四路四核的结构,因此采用1、2、4、8、16 和32个线程分别进 行并行处理并观察实验结果。

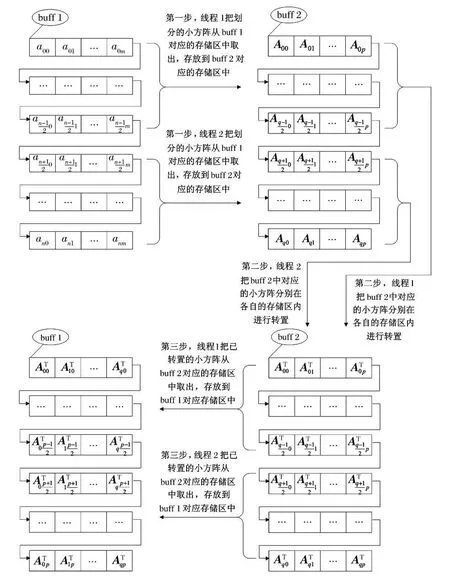
图7 多线程矩阵转置的处理过程Fig.7 Processing process of multi-thread matrix transposition

表1 多线程矩阵转置的实验结果Table1 Result of multi-thread matrix transposition

如上表所示,随着处理线程个数从1 递增到4,并行处理时间相应的减少,随着处理线程个数从4增加到32,并行处理时间反而小幅增加。

5.2 结论及分析

上面的实验结果说明,随着线程个数逐渐增大到4,多线程矩阵转置的并行处理所用的时间逐渐减少到最小值,但再增加线程个数,并行处理时间反而增加。这是由于本系统是4个处理器,每个处理器都是4 核的,当线程为4个、8个和16个时,所用的时间相差不大,8个和16个线程的处理时间有小幅增加,都比较充分地利用了处理器的资源。由于线程的建立、销毁和同步也要占用处理器资源,运行8个和16个线程利用处理器资源而节省的时间被这些线程的其他额外开销抵消了。但当线程数增加到32个时,由于超过了所有处理器的总核数,并行处理时间继续增加。

多线程矩阵转置的并行处理方法能有效地利用多处理器和多核的硬件资源,比传统的单线程和单进程的串行矩阵转置的效率更高,转置的正确性不会由于线程个数增加而发生变化,具有良好的并行扩展性,有利于进行快速的矩阵转置。随着通用计算机平台性能的不断提升,这种方法一定会在不久的将来具有更好的应用前景。

References)

[1]张冠杰,张涛,张欢阳,等.实时SAR成像中的高速矩阵转置算法及实现[C]//2005年中国合成孔径雷达会议:359-364

[2]谢应科,张涛,韩承德.实时SAR成像系统中矩阵转置的设计和实现[J].计算机研究与发展,2003(1):6-11

[3]贾韶旭,潘锦.多线程技术在探底雷达中的应用[C]//2007年全国微波毫米波会议:1953-1956

[4]李建军,陈鸿星,张红新.Linux 线程库的实现机制[J].计算机与现代化,2005(4):96-98,113

[5]师林.Linux 内核同步技术的基本原理及应用原则[J].计算机科学,2006(9):165-167

[6]孙东,方建勋,李廉登.实时应用中POSIX 信号灯技术研究[C]//中国计算机用户协会信息系统分会2005年信息交流大会:247-248,253

[7]黄道颖,张安琳.Linux系统对SMP 并行处理的支持[J].郑州轻工业学院学报(自然科学版),2001(4):26-30

[8]龙卉,皮亦鸣.合成孔径雷达并行成像算法研究及实现[D].成都:电子科技大学,2001