基于CQG2000的吉林省西部地区似大地水准面的建立
2010-12-25刘振宇高炳浩
刘振宇,高炳浩
吉林省基础地理信息中心,吉林长春130051
基于CQG2000的吉林省西部地区似大地水准面的建立
刘振宇,高炳浩
吉林省基础地理信息中心,吉林长春130051
针对CQG2000精度无法满足实际工作的情况,提出一种新的重力似大地水准面与GPS水准的拟合方法——残差模型法,利用CQG2000、较密集的 GPS水准点,采用残差模型法建立吉林省西部地区似大地水准面模型(Jilin west quasi-geoid,JLWQG)。论述建立JLWQG的三角剖分双线性内插算法及其适用性,检测结果表明,JLWQG精度达到了±0.05 m,JLWQG在吉林省西部地区基础测绘更新工作中进行了大面积的应用,取得了满意的结果。
CQG2000;残差模型法;吉林省西部地区似大地水准面;三角剖分双线性内插;应用
1 前 言
在吉林省西部地区基础测绘更新工作中,为了替代繁重的几何水准测量工作,需要将GPS测量得到的大地高精确地转化为正常高。吉林省西部地区已有最高精度的似大地水准面为CQG2000,其空间分辨率为5′×5′,精度为±0.3~±0.4 m。吉林省西部地区属于平原地区,为满足基础测绘更新工作的需要,要采用±0.1 m以上精度的似大地水准面。
吉林省西部地区存在数量较多的 GPS水准点,可以利用CQG2000、GPS水准点进行拟合计算,建立高精度的JLWQ G。目前,重力水准面与GPS水准点拟合计算一般采用高次多项式进行分区拟合;或者进行地形改正后,进行拟合计算。
2 残差模型法的原理
目前,建立高精度似大地水准面模型的方法有:利用高分辨率地面重力测量数据,按Molodensky理论求解扰动位;按Bruns公式确定重力似大地水准面模型;与由GPS水准测定的离散高程异常进行拟合,获得与国家正常高系统定义一致的似大地水准面。或者直接采用EGM2008等全球地球重力场模型,利用GPS水准网点的高程异常值作为控制,将全球模型进行校正,获得所需的似大地水准面模型。
似大地水准面模型的建立过程主要分为两步,首先建立重力似大地水准面;然后利用 GPS水准点进行拟合,进一步提高精度。单纯从高精度似大地水准面模型的结构上讲,包括两部分结构:其一是由重力数据建立的重力似大地水准面,具有分辨率高、相对精度高、绝对精度较低的特点;其二是由GPS水准测定的高程异常值构建的拟合曲面,具有绝对精度高、分辨率较低的特点。
建立吉林省西部地球重力场模型存在建设周期长、投入大的特点;EGM2008在吉林省还没有经过实际检验。因此针对似大地水准面的第二个结构特点,采用CQ G2000及吉林省西部地区较密集的GPS水准点,改善CQG2000高程异常值少、分辨率低的缺点(HACN90网点在吉林省西部地区只有两点),从而快速构建高精度的JLWQG。
基于CQ G2000建立JLWQG的残差模型法,主要步骤为:首先将 GPS水准测量获得的高程异常值与 CQG2000的高程异常值做差分计算,获得残差值,即移去CQG2000所携带的物理场信息
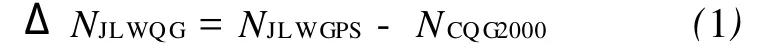
式中,ΔNJLWQG为JLWQG与CQG2000高程异常值之差;NJLWGPS为JLWQG高程异常值;NCQG2000为CQG2000高程异常值。
然后利用离散的残差值采用几何方法构造一个连续的数值模型,即拟合
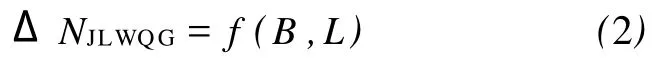
式中,f为需要构造的拟合函数;B,L为拟合点的纬度、经度。
最后,在连续的残差数值模型上叠加CQG2000,即恢复物理场信息,在CQG2000的基础上完成JLWQG的构建。

式中,NJLWQG为JLWQG的高程异常值,以待求点的经度、纬度为引数。
该方法克服了纯几何内插的缺陷,其仍是在物理面的基础上进行的内插,保留了全部的物理场信息,可靠性及精度更高。
3 测区及已有资料概况
吉林省西部地区总面积为3.5×104km2,占吉林省总面积的20%,地貌以平原为主,丘陵面积约占30%,平均海拔110~200 m之间,地势起伏变化很小。
吉林省西部地区共有130个GPS水准点,与CQG2000相比,GPS水准点的高程异常值精度要高一个数量级。对GPS水准点进行基准转换,统一至ITRF93框架,参考历元96.365。
4 算法分析
残差模型法的关键在于寻找数学算法,确定f(B,L),使其能准确的反映出 GPS水准面与CQG2000的差距。
根据物理大地测量学的理论,地球重力场由三部分组成,分别是长波分量,主要由地球整体质量分布决定;中波分量,主要由地壳的扰动质量分布决定;短波分量,主要由地形的扰动质量分布决定。其特点是长波分量占优,大于90%;中、短波分量相对偏小;短波影响很小,特别是在平原地区中、短波分量影响更小。长波分量是重力场谱结构的主分量,是“骨架”,从某种意义上说,精确确定重力场模型的长波分量,就是为模型提供了“牢固”和精密的框架,是基础。因此残差值主要是长波分量与真实的似大地水准面的差值,同时因长波分量的作用范围一般为上千千米,而测区面积相对较小,残差值在测区内会表现出系统误差的特性,即残差面应具有出如下特点:通过 GPS水准点,连续、均匀、平缓变化,不会出现异常点。
为使拟合曲面满足上述特点,数学算法应满足:残差值与坐标相关,满足拉格朗日插值条件,一次多项式曲面,曲面连续。
目前采用的拟合算法多为高次多项式分区拟合,容易导致如下问题:拟合多项式阶次过高,则拟合曲面形态过于复杂,长波分量的骨架作用得不到体现,且拟合面边缘地区会出现剧烈的“振荡”现象;拟合多项式阶次过低,GPS水准点使用率较低,导致其携带的高精度信息利用率较低,中、短波分量信息体现不明显。由此进一步发展分区拟合的思想,采用三角剖分双线性内插法进行拟合,其基本原理为:首先以 GPS水准点为节点,将整个拟合区剖分成一个个小的三角形,保证三角形覆盖整个测区,没有重叠区域;然后以三角形顶点为插值点,采用双线性内插法对每个小三角形区域进行内插计算,并保证相邻三角形边具有相同的插值。
5 算法实现
选择分布较为均匀的83个 GPS水准点参与计算,其余47点用于外部检核。其与CQG2000差分计算结果如表1。
残差值的数学期望为+0.332 m,中误差为±0.345 m。其系统误差是长波分量误差的体现。
以这83个残差点为节点,采用Delaunay准则将整个测区剖分成小的三角形区域。三角剖分是将一个散点集合剖分成不均匀的三角形网格。Delaunay,三角剖分满足两个重要的准则:空圆准则,网中任一三角形的外接圆范围内不会有其他点存在;最大化最小角准则,其所形成的三角形的最小角最大。采用Delaunay准则进行三角剖分,具有如下特性:最接近性,以最近临的三点形成三角形,且各线段皆不相交,可保证拟合结果具有最高的空间相关性;唯一性,剖分结果唯一;最优性,任意两个相邻三角形形成的凸四边形的对角线如果可以互换的话,那么两个三角形六个内角中最小角不会变大,避免内插时形成病态方程;区域性,即改变任意节点只会影响临近三角形,保证误差不会整网传递;具有凸多边形外壳,即最外层可形成一个凸多边形外壳,保证拟合区覆盖整个测区。整个测区的三角剖分结果见下图:

表1 残差表Tab.1 Residual value /m
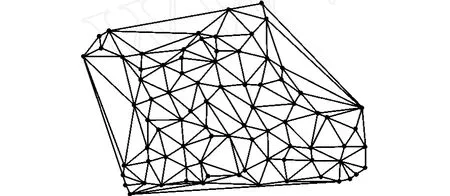
图1 Delaunay三角剖分示意图Fig.1 Sketch map of delaunay triangulation
然后对每个小三角形进行拟合计算,计算采用双线性内插法,保证每个小三角形平缓均匀变化,相互之间接边。其实用数学模型为
设三角形的三个顶点为A、B、C,点l、点r分别位于AB、A C上,点 P为直线lr上的一点,则点 P的拟合值 HP计算公式为
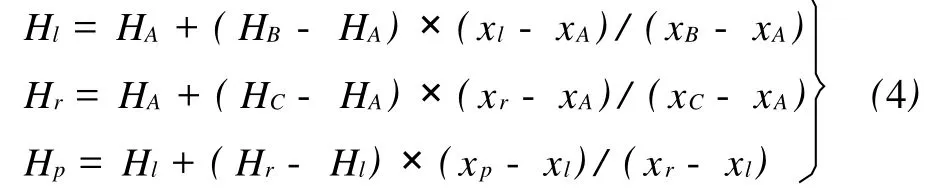
其中,yP=yl=yr。
最后将CQG2000、拟合曲面进行叠加,建立JLWQG。
在实际工作中,还比较了多项式拟合法、按距离定权插值法,计算结果都没有三角剖分双线性内插法理想。
6 外部检核
以测区内没有参加运算的47个GPS水准点作为外部检核点,其几何水准高程与利用JLWQG内插计算获得的高程相比较结果见表2。
精度统计分析:数学期望为-0.002 m,中误差为±0.054 m。
7 结 论
JLWQG的空间分辨率为5′×5′,与CQG2000相比较精度由±0.3~±0.4 m提高到±0.05 m。2009年11月采用JLWQG内插计算了2 336点的正常高,经检验计算结果满足基础测绘更新工作的需要,提供使用后取得了满意的结果。
吉林省西部地区基础测绘更新工作采用JLWQG后,统一采用GPS技术进行平面、高程测量,提高了作业效率,节约作业成本约500余万元。
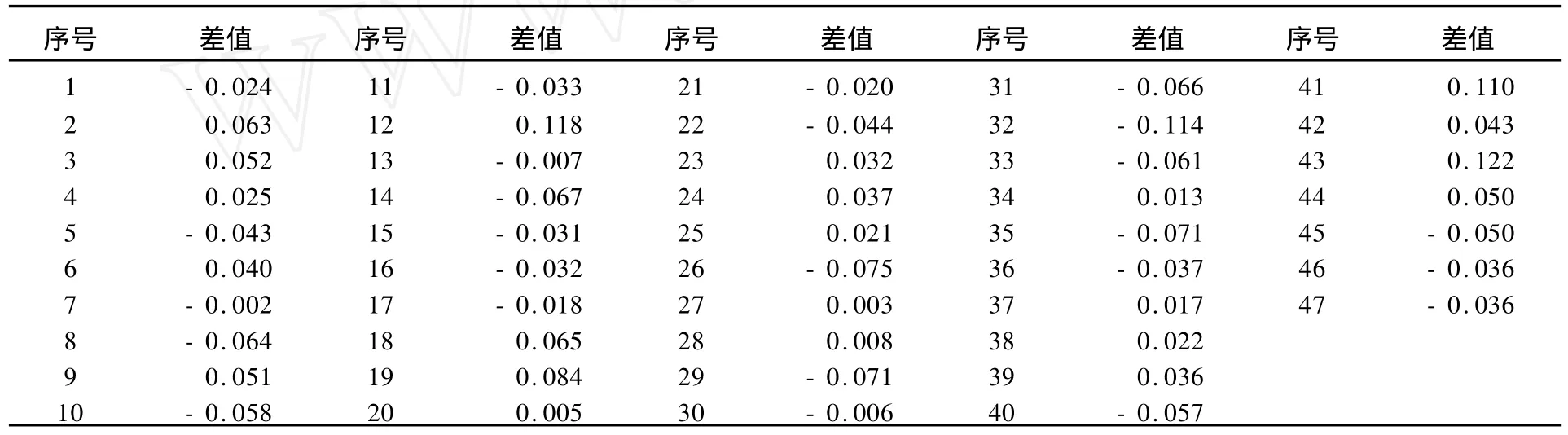
表2 外部检核点差值表Tab.2 D-value of independent points /m
[1] LI Jiancheng,CHEN Junyong,NING Jinsheng,et al.The Approximation Theory of Earth Gravity Field and Determination ofChina Quasi-Geoid2000[M].Wuhan:Wuhan University Press,2003.(李建成,陈俊勇,宁津生,等.地球重力场逼近理论与中国2000似大地水准面的确定[M].武汉:武汉大学出版社,2003.)
[2] ZHANG Chuanyin,GUO Chunxi,CHEN Junyong,et al. EGM2008 and Its Application Analysis in Chinese Mainland[J].Acta Geodaetica et Cartographica Sinica,2009,38 (4):283-289.(章传银,郭春喜,陈俊勇,等.EGM2008地球重力场模型在中国大陆适用性分析[J].测绘学报,2009, 38(4):283-289.)
[3] LI Chong,ZHANG Qin,LIU Zhanke.Gain the Elevation Abnormality by the Method of RCR Based on CQG2000 [J].Bulletin of Surveying and Mapping,2007,10:4-6.(李冲,张勤,刘站科.基于CQG2000采用RCR法求解高程异常[J].测绘通报,2007,10:4-6.)
Establishing the Jilin West Quasi-Geoid Based on CQG2000
LIU Zhenyu,GAO Binghao
Jilin Basic Geography Information Center,Changchun 130051,China
As the precision of CQG2000 cannot meet the need of practical work,a residual model method of combining gravity quasi-geoid and GPS level has been presented.Based on CQG2000 and GPS level points with comparatively high density,the Jilin West Quasi-Geoid(JLWQG)is determined by this residual model method.This paper also discussed the triangulation bilinear interpolation algorithm and its applicability for JLWQG.The study shows that the precision of JLWQGis up to±0.05 m.And JLWQG is widely and efficiently used in the renewal of basic surveying and mapping in the west of Jilin.
CQG2000;residual model method;Jilin west quasi-geoid(JLWQG);triangulation bilinear interpolation algorithm;application
LIU Zhenyu(1976—),male,B.E,engineer, majors in application to geodesy and gravity field of the Earth.
1001-1595(2010)05-0441-03
P223
A
(责任编辑:张燕燕)
2010-01-12
2010-04-11
刘振宇(1976—),男,学士,工程师,目前主要从事大地测量与地球重力场应用研究工作。
E-mail:liuzhenyu_2000@163.com
