顾及转向延误的时间依赖A＊最短路径算法

郑年波,陆 锋,李清泉,段滢滢

1.中国科学院地理科学与资源研究所资源与环境信息系统国家重点实验室,北京100101;2.武汉大学交通研究中心,湖北武汉430079

顾及转向延误的时间依赖A＊最短路径算法

郑年波1,陆 锋1,李清泉2,段滢滢1

1.中国科学院地理科学与资源研究所资源与环境信息系统国家重点实验室,北京100101;2.武汉大学交通研究中心,湖北武汉430079

建立基于路段的时间依赖网络模型,将转向延误时间引入到FIFO(先进先出)条件的定义中,并给出满足FIFO条件的路段到达时间和转向延误时间计算式。通过将时间因子引入到启发式评价函数中,发展了基于路段标号的时间依赖A＊最短路径算法。试验表明,所提出的算法能预测并回避即将发生的交通拥堵,有效节省用户的出行时间。而其平均计算时间仅比传统算法增加10%左右。由于不再需要进行频繁的路径重优化,该算法能提高路径规划的整体效率。

路径规划;最短路径;A＊算法;时间依赖网络;转向延误

1 引 言

利用交通信息进行动态路径规划是车辆导航、位置服务等研究领域的重要课题[1]。而目前相关算法只是简单地将当前交通信息作为路段权值调整的系数,于出发前利用各种启发式最短路径算法计算最优行驶路径[2],并于行驶过程中利用实时接收的交通信息进行路径的重计算[3]。它们忽略了路段行程时间依赖于进入该路段的时刻这一现实,不能从出行全局上为用户考虑,导致频繁的路径重计算,进而影响导航系统的整体效率。有必要研究时间依赖的最短路径算法。

时间依赖最短路径问题将路段行程时间建模为时间依赖的变量,并在满足先进先出条件的情况下,可以通过改进的Dijkstra、A＊等标号设定(label-setting,LS)算法来求解[4-9]。然而,这些改进的算法普遍缺乏对交叉口转向延误的考虑。事实上,交叉口转向引起的时间延误可以达到全部行驶时间的17%～35%[10]。同一交叉口不同的转向通常有不同的延误时间,这与LS算法单一标号的性质相矛盾,基于节点标号的LS算法不再有效[11]。针对此问题,路段标号和对偶图法是两种有效的解决策略[10-17]。这些方法都基于静态网络,缺乏对交通网络时间依赖特性的考虑。事实上,转向延误的存在影响了时间依赖网络的FIFO条件,需要考虑对之进行重新定义。

本文面向带转向延误的时间依赖最短路径问题,定义基于路段的时间依赖网络以及考虑转向延误的FIFO条件,发展基于路段标号的时间依赖A＊算法。

2 基于路段的时间依赖网络模型

基于路段的时间依赖网络模型定义如下: GL=(L,U,W,D)。其中,L={0,1,…,n-1}表示有向路段集。U⊆{(i,j)|(i,j)∈L×L,e(i)=s(j)}表示转向集,其中e(i)表示路段 i的终止节点,s(j)表示路段j的起始节点。W={wi(t)|i∈L,t∈T}表示时间依赖路段行程时间集,其中wi(t)表示t时刻在路段i上的行程时间,T表示时间集。D= {dij(t)|(i,j)∈U,t∈T}表示时间依赖转向延误时间集,其中,dij(t)表示 t时刻于交叉口(即e(i)或s(j))处由路段i转向路段j的延误时间。

设 ai(t)表示t时刻从节点s(i)出发沿路段i到达其相邻节点e(i)的时间,有ai(t)=t+wi(t)。设rij(t)表示t时刻从节点s(i)出发沿路段i转入相邻路段j的时间,有

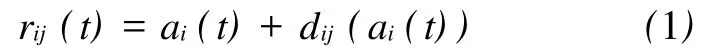
设 p={i1,i2,…,im}(m>1)为路段 i1到路段im的一条路径,其中,e(i1)=s(i2),…,e(im-1) =s(im),则其到达时间定义如下

设 P(o,d)为路段 o到路段 d的所有路径, EAod(t)为 t时刻从路段o出发最早到达路段 d的时间,则有 EAod(t)=min{ap(t):p∈P(o,d)}。计算 EAod(t)的过程也就是求解 o-d时间最短路径的过程。

FIFO条件 对于网络中的每一个转向(i,j)∈U,如果 rij(t)非减,即

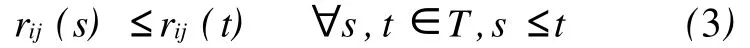
则称网络满足先进先出(first in first out, FIFO)条件。文献[4]指出,FIFO网络中的最短路径问题可以使用改进的Dijkstra、A＊等算法来求解。根据公式(1),要使不等式(3)成立,则路段到达时间函数ai(t)与转向延误函数dij(t)必须同时满足FIFO条件,即

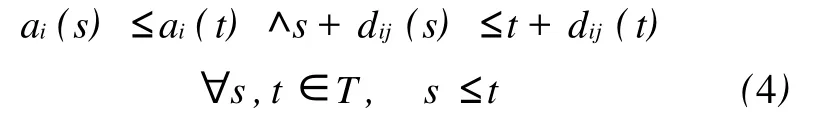
3 满足FIFO条件的路段到达时间与转向延误时间

3.1 路段到达时间

在对路段i∈L的交通状况进行建模时,通常将连续时间 T划分成若干时段[t0,t1),…,[tf-1, tf),并认为每个时段[tk,tk+1)内的交通流速度 vk稳定。这样,路段上的一个行程可能跨越速度值不同的多个时段,其满足FIFO条件的到达时间ai(t)计算如下(其中 l表示路段i的长度)[5]

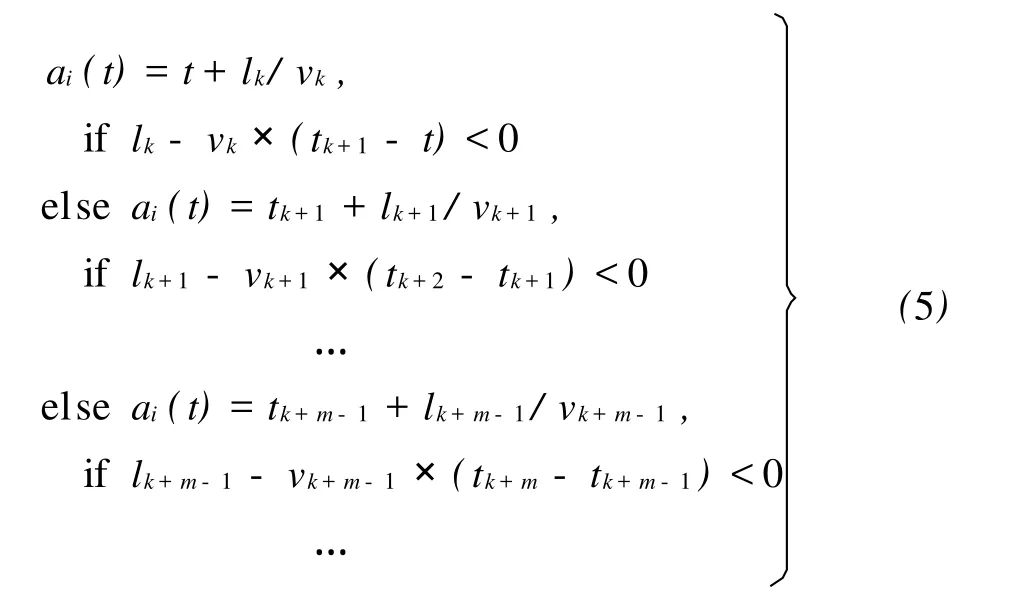
式中,

3.2 转向延误时间

在处理转向延误时间时,也将连续时间 T离散化为多个时段[t0,t1),…,[th-1,th),并认为每个时段[tk,tk+1)内的平均延误时间恒定为 ck(ck值的确定是交通工程学中交通流理论研究的重要内容)。这样,车辆实际的转向延误时间可通过如下公式来计算

此计算过程考虑了跨越两个时段的情况(现实应用中转向等待不太可能跨越两个以上时段),能保证先排队的车辆先转入下一条路段,即满足FIFO条件。

4 基于路段标号的时间依赖A＊算法

A＊最短路径算法以启发式评估函数作为节点标号,通过赋予位于最短路径上可能性高的节点以高的优先级,来达到缩减搜索空间的目的[2]。在基于路段的时间依赖网络中,启发式评估函数定义为

式中,t为出发时间;ap→i(t)为沿评估路径 p到达当前路段i的时间(根据式(2)计算);e(i,d)(ap→i(t))为ap→i(t)时刻从当前路段i到目标路段d的行程时间的估计。启发式函数 e(i,d)(ap→i(t))的设定则是一个事关算法效率的关键性问题。如果其值不超过相应的实际最小行程时间(即满足可纳性),则能保证找到数学最优解[7]。鉴于此,本文令

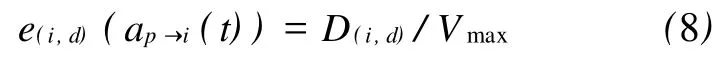
式中,D(i,d)为当前路段 i到目标路段d的欧式距离(通过节点e(i)和节点e(d)的坐标计算而得); Vmax为所有路段最大可能的行车速度。

基于路段标号的时间依赖A＊(time-dependent A＊,TDA＊)算法的基本思想如下:从起始路段出发,循环从候选路段集中选取标号 Fi(t)最小的路段扩展生成后续路段并更新其标号值,标号更新后的路段作为下一次的选取对象再插入到候选路段集中。设o为起始路段,d为终止路段,t为从节点s(o)出发的时间,Pi为路段i在路径上的直接前驱路段,Q为候选路段集,R为永久标号路段集(到此集合中的路段的最短路径已经找到),则TDA＊算法的流程如下(其中,A rrival(i,t)为基于式(5)的路段到达时间计算函数,Turn(i,j,t)为基于式(6)的转向延误时间计算函数):

1.初始化。令 ap→o=A rrival(o,t),Fo= ap→o+D(o,d)/Vmax,Fj=ap→j= ∞ ∀j≠o,Po= -1,Q={o}。

2.路段选择。从候选路段集Q中选出Fi值最小的路段i,并将之永久标号,即:

如果i==d,则目标路段已找到,循环终止。否则:

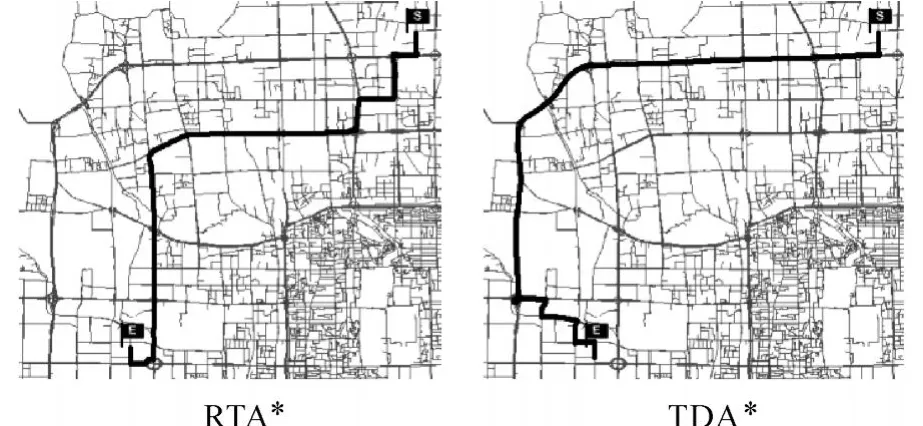
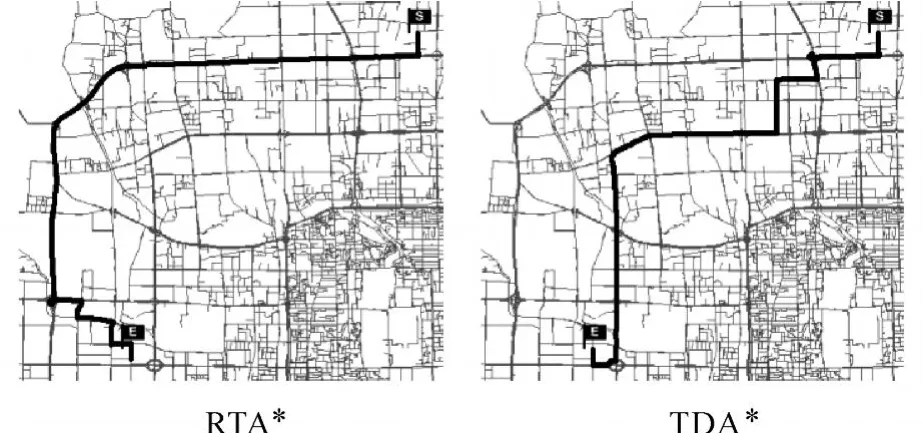
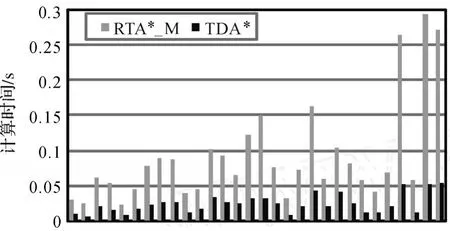
3.路段扩展。对于路段i的每一条后继路段j∈L,(i,j)∈U,如果它还未永久标记,即 j∉R,且ap→i+Turn(i,j,ap→i)+A rrival(j,ap→i+Turn(i, j,ap→i))+D(j,d)/Vmax

4.搜索终止。如果所有路段都扩展完,即Q=∅,则终止循环;否则转向步骤2。

5 试 验

本文在课题组自主开发的城市公众出行路径规划服务系统为试验平台(双核CPU 1.6 GHz,内存1.0 GB,操作系统Windows XP professional SP3)上对所提出的算法进行了验证与测试。

5.1 数据准备

试验路网采用北京市四环以内双线表达的导航路网,共有路段25 602条(交叉路口处的虚拟路段和虚拟节点概化为单一的拓扑节点)。交通数据采用北京市2007年7、8、9三个月的以5 min为周期的浮动车实测车速数据,一天分为288个时段。考虑到交通流的周期性变化规律,对所有属于同一日期类别同一时段的速度值进行平均化处理,形成了从星期一到星期日的7个速度数据集。目前的交通数据中,共有4 929条路段有交通信息,基本上覆盖了主要道路。而对于交通信息不能覆盖的路段,根据道路类型和进入时间设置默认速度值如表1所示。

表1 预定义的道路速度Tab 1 Predefined speeds on different road types /(km/h)

另外,考虑到准确可用的转向延误数据难以获得,作者从交叉口绿信比的角度考虑,以时段和转向类型为依据,为所有转向建立了一个简单的延误模型:fij(t)=0.5×g(t,ty peij)(见3.2节)。其中,0.5表示交叉口等待的概率,g(t,ty peij)的取值如表2所示。

表2 简单的时间依赖转向延误模型Tab.2 A naive model for time-dependent turn delays /min

5.2 算法准备

TDA＊算法使用四叉堆优先级队列来实现候选路段集[18],并基于经验将所有路段的最大可能行车速度设置为60 km/h。为了算法比较的需要,作者实现了 RTA＊(real-time A＊)算法和RTA＊_M算法。RTA＊算法是指仅考虑出发时刻交通信息的A＊算法,它与静态A＊算法的区别仅在于以当前交通信息而不是长度/限速作为路段的权值。RTA＊_M算法是指整个导航过程中的多次RTA＊算法调用。该算法的基本流程如下:①出发前利用RTA＊算法计算一条最优路径;②沿着规划路径行进,每当有新的交通信息到来时(根据历史交通数据进行模拟,以每5 min为一个周期),调用 RTA＊算法计算新的路径;③步骤②循环直至抵达目的地。RTA＊_M算法的计算时间为多次RTA＊算法计算时间的和,路径为多次重计算后完整的行车路径。

5.3 试验结果与算法分析

为了验证TDA＊算法的有效性,选取北辰东路为起始路段,翠微路为终止路段,设置出发时间为周二上午7:00和8:00,分别利用 TDA＊算法和RTA＊算法进行计算,结果如图1和图2所示。

图1 TDA＊算法与RTA＊算法计算结果的比较(出发时间:7:00)Fig.1 Comparison of computational results of TDA＊and RTA＊(departure time:7:00)

图2 TDA＊算法与RTA＊算法计算结果的比较(出发时间:8:00)Fig.2 Comparison of computational results of TDA＊and RTA＊(departure time:8:00)

从图1可以看出,7:00出发时,TDA＊算法预测出车辆到达时刻三环路上将发生交通拥堵,因此建议绕道四环以避之。而RTA＊算法由于只考虑当前时刻的交通状况,因此当车辆沿其规划的路径到达三环路上时,将会遇到交通拥堵。

从图2可以看出,8:00出发时,三环路上正好发生交通拥堵,RTA＊算法基于此建议走四环以避之,而事实上,当车辆到达三环路时,交通拥堵状况可能已经缓解。与此相反,TDA＊算法在出发时就预测到三环路上拥堵状况即将缓解的趋势,因此建议一条看似拥堵而实际并不拥堵的路径(即三环路),有效地避免了不必要的绕道。

为了测试TDA＊算法的效率与精度,以周二上午7:30为出发时间,从网络中任意选取30对OD路段,分别利用 TDA＊算法、RTA＊算法和RTA＊_M算法计算每对OD间的时间最短路径。结果如图3、图4和图5所示(横轴表示30条按长度从小到大排序的路径)。

图3 TDA＊算法与RTA＊_M算法所计算路径行程时间的比较Fig.3 Comparison of travel times of computational paths of TDA＊and RTA＊_M

图4 TDA＊算法与RTA＊算法计算时间的比较Fig.4 Comparison of computational times of TDA＊and RTA＊

从图3可以看出,总体而言,相比于RTA＊_ M算法,TDA＊算法所计算路径的行程时间更短。不过这种优势并不明显,主要原因在于: RTA＊_M算法也考虑了回避交通拥堵的情况,在经过多次路径调整后,RTA＊_M算法所得路径的行程时间比 TDA＊算法所得路径的行程时间多得有限,这种现象在路段行车速度长时间没有大的变化的情况下,表现得更为明显。当然,交通信息覆盖率不高、行程时间预测模型与转向延误模型存在一定的误差等也是一部分影响因素,但影响大小的定量测试需要高质量交通数据以及准确的行程时间预测模型和转向延误计算模型的支持。

图5 TDA＊算法与RTA＊_M算法计算时间的比较Fig.5 Comparison of computational times of TDA＊and RTA＊_M

从图4可以看出,TDA＊算法的计算时间比RTA＊算法略有增加,平均幅度大约为10%。其中多出的时间主要用于路段到达时间和转向延误时间的计算。

从图5可以看出,TDA＊算法的计算时间远少于RTA＊_M算法。原因在于导航过程中需要多次调用RTA＊算法以进行路径的优化与重优化,而TDA＊算法由于预先考虑了到达时刻路段的交通状况,整个导航过程只需一次调用即可。可见,TDA＊算法有助于降低导航过程中路径规划的频率,从而提高导航系统的整体效率。

6 结 论

面向带转向延误的时间依赖最短路径问题,本文通过定义基于路段的时间依赖网络模型,并将转向延误引入到FIFO条件的定义中,发展了基于路段标号的时间依赖A＊最短路径算法。该算法能预测并回避即将发生的交通拥堵,有效节省用户出行时间、提高导航系统整体运行效率,具有较强的实用价值。

TDA＊算法的精度和可用性与行程时间数据和转向延误数据的准确性直接相关,本文只是简单对历史交通数据作了均化处理,转向延误使用的也仅是经验值。在后续工作中将深入探讨准确可用的路段行程时间预测模型与交叉口转向延误计算模型。

[1] LU Feng,ZHENG Nianbo,DUAN Yingying,et al.Travel Information Services:State of the Art and Discussion on Crucial Technologies[J].Journal of Image and Graphics, 2009,14(7):1219-1229.(陆锋,郑年波,段滢滢,等.出行信息服务关键技术研究进展与问题探讨[J].中国图象图形学报,2009,14(7):1219-1229.)

[2] FU L,SUN D,RILETT L R.Heuristic Shortest Path Algorithms for Transportation Applications:State of the Art[J].Computers&Operation Research,2006,33(11): 3324-3343.

[3] HUANG B,WU Q,ZHAN F B.A Shortest Path Algorithm with Novel Heuristics for Dynamic Transportation Networks[J]. InternationalJournalof Geographical Information Science,2007,21(6):625-644.

[4] KAUFMAN D E,SMITH R L.Fastest Paths in Timedependent Networks for Intelligent Vehicle-Highway Systems Application[J].Journal of Intelligent Transportation Systems,1993,1(1):1-11.

[5] SUNG K,BELL M G H,SEONG M,et al.Shortest Paths in a Network with Time-dependent Flow Speeds[J].European Journal of Operational Research,2000,121(1): 32-39.

[6] HORN M.Efficient Modeling of Travel in Networks with Time-Varying Link Speeds[J].Networks,2000,36(2): 80-90.

[7] CHABINI I,LAN S.Adaptations of the A＊Algorithm for the Computation of Fastest Paths in Deterministic Discrete-Time DynamicNetworks[J]. IEEE Transactions on Intelligent Transportation Systems,2002,3(1):60-74.

[8] KANOULAS E,DU Y,XIA T,et al.Finding Fastest Paths on a Road Network with Speed Patterns[C]∥Proc of the 22nd International Conference on Data Engineering. Washington D C:IEEE Computer Society,2006.

[9] NANNICINI G,LIBERTI L.Shortest Paths on Dynamic Graphs[J]. International Transactions in Operational Research,2008.15(5):551-564.

[10] HAN Gang,J IANGJie,CHEN Jun,et al.An Arc Based Dijkstra Algorithm for Road Turning Penalty in Vehicle Navigation System[J].Acta Geodaetica et Cartographic Sinica,2002,31(4):366-368.(韩刚,蒋捷,陈军,等.车载导航系统中顾及道路转向限制的路段Dijkstra算法[J].测绘学报,2002,31(4):366-368.)

[11] REN Gang,WANG Wei,DENG Wei.Shortest Path Problem with Turn Penalties and Prohibitions and Its Solutions[J].Journal of Southeast University:Natural Science Edition,2004,34(1):104-108.(任刚,王炜,邓卫.带转向延误和限制的最短路径问题及其求解方法[J].东南大学学报:自然科学版,2004,34(1): 104-108.)

[12] CALDWELL T.On Finding Minimum Routes in a Network with Turn Penalties[J].Communications of the ACM, 1961,4(2):108.

[13] ZHENG Nianbo,LI Qingquan,XU Jinghai,et al.A BidirectionalHeuristic ShortestPath Algorithm with Turn Prohibitionsand Delays[J]. Geomaticsand Information Science of Wuhan University,2006,31(3): 256-259.(郑年波,李清泉,徐敬海,等.基于转向限制和延误的双向启发式最短路径算法[J].武汉大学学报:信息科学版,2006,31(3):256-259.)

[14] GAO Song,LU Feng.An Arc-labeling Shortest Time Path Algorithm[J].Geo-Information Science,2008,10 (5):604-610.(高松,陆锋.基于路段标记的交通网络时间最短路径算法[J].地球信息科学,2008,10(5): 604-610.)

[15] GUTIÉRREZ E,MEDAGLIA A L.Labeling Algorithm for the Shortest Path Problem with Turn Prohibitions with Application to Large-scaleRoad Networks[J]. Annals of Operations Research,2007,157(1):169-182.

[16] AÑEZ J,DE LA BARRA T,PÉREZ B.Dual Graph Representation of Transport Networks[J].Transportation Research Part B:Methodological,1996,30(3): 209-216.

[17] WINTER S.Modeling Costs of Turns in Route Planning [J].GeoInformatica,2002.6(4):345-361.

[18] LU Feng,LU Dongmei,CUI Weihong.Improved Dijkstra Algorithm Based on Quad-Heap PriorityQueueand Inverse Adjacent List[J].Journal of Image and Graphics, 1999,4A(12):1044-1050.(陆锋,卢冬梅,崔伟宏.基于四叉堆优先级队列及逆邻接表的改进型Dijkstra算法[J].中国图象图形学报,1999,4A(12):1044-1050.)

The Adaption of A＊Algorithm for Least-time Paths in Time-dependent Transportation Networks with Turn Delays

ZHENGNianbo1,LU Feng1,LI Qingquan2,DUAN Yingying1
1.State Key Laboratory of Resources and Environmental Information System,Institute of Geographic Sciences and Natural Resources Research,Chinese Academy of Sciences,Beijing 100101,China;2.Transportation Research Center,Wuhan University, Wuhan 430079,China

A link-based time-dependent network model was built by introducing the turn delay time into the definition of“first in first out(FIFO)”condition.A link-labelling time-dependent A＊shortest path algorithm is developed by adapting temporally the heuristic evaluationfunction and using Euclidian distance divided by maximum possible driving speed as the heuristic evaluator.An experiment on the real road network showed that the proposed algorithm is capable of forecasting and bypassing those forthcoming traffic congestions and then shortening travel time,only with a cost of about 10%more computational time than the traditional algorithms.Moreover,it is able to improve overall efficiency of route planning heavily because the frequent path re-optimization processes are no longer needed.

route planning;shortest path;A＊algorithm;time-dependent network;turn delay

ZHENG Nianbo(1979—),male,postdoctoral,majors in geographic information systems for transportation,intelligent transportation systems and spatial information services.

1001-1595(2010)05-0534-06

P208

A

国家863计划(2007AA12Z241);国家自然科学基金(40871184,40830530);中国博士后基金(20090450563)

(责任编辑:丛树平)

2009-09-14

2010-01-07

郑年波(1979—),男,博士后,主要从事GIS-T、ITS、空间信息服务等研究。

E-mail:zhengnb@lreis.ac.cn