利用GPS速度场估算青藏高原地壳韧性层等效粘滞系数分布的研究

杨 强,党亚民,3

1.武汉大学测绘学院,湖北武汉430079;2.中国测绘科学研究院大地测量与地球动力学研究所,北京100039;3.山东科技大学,山东青岛266510

利用GPS速度场估算青藏高原地壳韧性层等效粘滞系数分布的研究

杨 强1,2,党亚民1,2,3

1.武汉大学测绘学院,湖北武汉430079;2.中国测绘科学研究院大地测量与地球动力学研究所,北京100039;3.山东科技大学,山东青岛266510

将青藏高原及周边区域地壳分为脆性层和韧性层,并假定脆性层地壳近似弹性,韧性层为粘弹性层。利用 GPS水平速度场计算地面应变场,推导地壳内部作用力在不同点产生应变率之间的关系公式。利用稳态热传导方程估算地壳内部温度场,利用破裂强度和蠕变强度相等估算脆性-韧性转换面,并进一步估算青藏高原地壳不同深度的粘滞系数分布。结果表明,青藏高原及周边区域脆性-韧性转换面一般位于中地壳,深度分布在22～37 km之间,地壳较厚的区域转换层也较深;韧性层内粘滞系数分布,在中地壳约为1019～1022Pa·s,下地壳约为1017～1020Pa·s,Moho面则降至1016～1018Pa·s。

GPS速度场;脆性-韧性转换层;温度场;应变率;等效粘滞系数

1 引 言

在常压和室温下,大多数岩石是脆性的,即在破裂之前,其性能接近弹性。随着深度的增加,岩石圈由脆性转为韧性。压力、温度和应变率是确定岩石从脆性到韧性转化的重要因素[1]。在大陆动力学研究中,韧性地壳的存在和流动被认为是了解许多问题(包括青藏高原动力学演化)的关键[2]。从20世纪70年代开始,许多学者便开始了岩石圈流变性质的研究[3-5],逐渐提出了岩石圈流变强度分层的概念,引起了地学界的注意。

青藏高原是世界上海拔最高、最年轻、动力学环境最为复杂的高原,也是地球动力学的研究热点。青藏高原下地壳粘滞系数究竟是多少,已成为深入定量研究中突出的问题,它的数值量级将极大地影响定量模拟的结果。张晁军等分别利用流变定律和GPS求得的应变速率、模拟昆仑山地震震后变形、对炉霍地震震后跨断层形变曲线拟合等三种方法计算了青藏高原下地壳的粘滞系数[6]。Hilley等用地震复发周期方法得到的青藏高原下地壳粘滞系数在1018～1021Pa·s之间[7]。这些方法和成果,有助于更深入地认识和研究大陆岩石圈的等效粘滞系数,但由于使用的数据和方法不同,在结果上差异较大,其含义也不相同,在比较分析时应注意。

本文在前人研究成果基础上,利用GPS地面水平速度场,计算了地面应变。推导了地壳内部作用力引起两点应变之间的关系公式,计算了地壳内部温度场的分布,根据岩石破裂强度与蠕变强度公式估算了青藏高原地壳脆性-韧性转换面分布,并进一步计算了韧性层不同深度等效粘滞系数的分布。

本文所采用的地壳分层、各层地壳深度以及密度都来源于Crust2.0模型。Crust2.0是一个2°×2°的全球地壳模型。它提供了①冰;②水;③软沉积层;④硬沉积层;⑤上地壳;⑥中地壳;⑦下地壳,共七层的深度、密度、P波和S波的传播速度等。数据来源于http:∥mahi.ucsd. edu/Gabi/crust2.html。

2 脆性-韧性转换深度分布的研究

确定地壳脆性-韧性转换深度是研究地壳流变性质随深度变化的一个关键问题。目前对地壳脆性-韧性转换的详细过程仍然未知,因此在对此问题的研究中多采用实验数据和方法。由于缺乏完整的实验结果,所以对转换面的确定有着不同的观点和标准。Shimada等认为破裂强度和蠕变强度相等处为脆性-韧性转换深度[4],臧绍先等认为以此方法来确定脆性-韧性转换的深度在目前是比较合理和可行的做法[5]。本文采用破裂强度和蠕变强度相等方法估算脆性-韧性转换面深度。

岩石蠕变强度可以表达为[5]

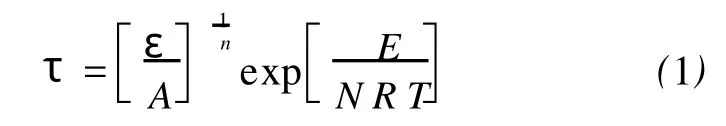
其中,τ为剪应力;ε为应变率;T为绝对温度;R为普适气体常数;E为激活能;A,N为独立于温度和压力的岩石流变参数。

岩石破裂强度随温度变化的关系较为复杂,涉及脆性向韧性转化及应变率,尚需更深入研究。但一般的结论是随着温度的增加脆性破裂强度非线性地减小。王威等[8]利用花岗岩围压在0～1 000 MPa、温度在20℃～850℃,辉长岩围压在250～800 MPa、温度在25℃～850℃的实验结果,得到破裂强度与围压和温度的关系为

这里,K,n,Ts,l均为常数,不同岩石取值不同;C为破裂强度;C0是岩石的单轴抗压强度;σc=ρgh为围压,ρ为岩石圈密度,g为重力加速度,h为深度。

令

求得的深度即为脆性-韧性转换深度h。由于很难直接利用公式(3)计算 h,所以本文采用的是逼近法,即将不同深度值 h代入公式,逐步缩小范围,如果取h1,h2时C-τ发生正负号变化,则在h1～h2之间进一步缩小步长,再次逼近。最终取一个h满足|C-τ|小于某个较小值e时(实际计算时e为0.1～1.0 Mpa,其中e取0.5 MPa时能够满足大多数区域的计算要求),得到转换深度h。注意,因为式(3)无法直接满足,得到的结果只是估值。

岩性是影响岩石粘度结构的首要因素。在研究大陆岩石圈流变结构时,必须首先对地壳内部岩石结构进行研究分析。Rudnick等人通过对全球地壳研究的综合分析认为,中地壳由基性、中性、酸性角闪片麻岩混合构成,下地壳以基性麻粒岩为主要组分[9]。然而,即使对地壳岩石组成有了充分的了解,在研究流变结构时一般并没有特定研究地区岩石的流变实验结果。即使是相同种类岩石,采自不同的地区,不同的研究者进行流变实验,得到的流变参数也会存在差异[13]。本文对此问题暂不讨论,采用前人的成果[8-13],表1给出了本文计算中所需参数的值。

表1 青藏高原脆性-韧性转换面参数Tab.1 Parameters of brittle-ductile transition plane in Tibetan Plateau

从上述公式中可以看出,要计算转换面深度,必须知道应变率和温度场。下面介绍本文所采用应变率和温度场。

2.1 温度场

地壳内部脆性-韧性的转化与温度密切相关,因此本文首先对地壳内部温度场分布进行研究。确定地壳温度分布最理想的情况是利用稳态的三维热传导方程,但是在实际应用中,三维热传导方程需要参数精确的三维空间变化情况及分布结果,而实际观测到的地表热流点往往较为稀疏,生热率及热传导的资料更少,这使得三维热传导方程的应用较为困难。因此,本文采用一维稳态方程来定地壳内部温度场的分布。其一维稳态热传导方程的基本形式为

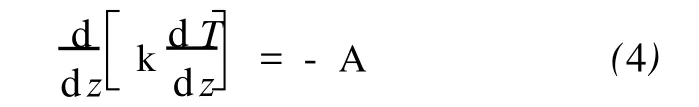
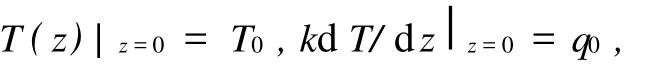
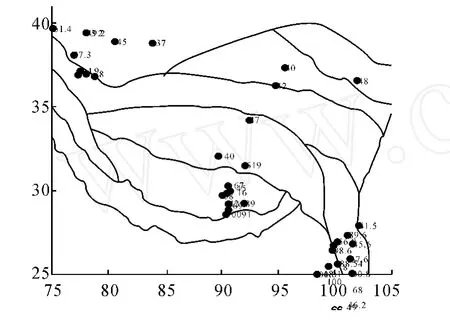
图1 青藏高原热流点分布Fig.1 Heat flow of Tibetan Plateau

沉积层和上地壳的生热率参数来自Wang[14-15],其他热导率和生热率来自安美建等[16],中地壳的生热率取0.4μW·m-3;下地壳生热率取0.1μW·m-3。上地壳热导率随深度和温度变化的关系式3.0×(1+0.001 5D)/(1+ 0.001 5T)W·m-1·K-1,其中D为深度(km), T为温度(℃)。其他各层热导率采用了固定值,分别为:沉积层的热导率为2.5 W·m-1·K-1;中地壳为2.25 W·m-1·K-1;下地壳取2.0 W· m-1·K-1。

温度场计算中,本文利用汪洋等提供的青藏高原各构造单元的地壳30 km温度为约束[15],反算地表热点值,并与地表热流插值结果进行比较,发现二者大部分数值误差在25%以内,标准差较高,为±37.46,标准差较高的原因主要是因为数据中有几个孤高热流点,如(29.828 33,90.316 67)点的热流为271,(31.498 33,92.05)点为319等。将数值过大的几个热流去除后,误差降低,标准差降为±18.56。

2.2 应变率场

岩石强度和等效粘滞系数与应变率有关,计算中必须给出应变率。目前,许多研究人员根据地表的GPS观测数据计算了中国大陆地表水平应变场[17-19]。使用块体整体旋转与线性应变模型,利用GPS速度场可以反演块体旋转和应变参数[10]:

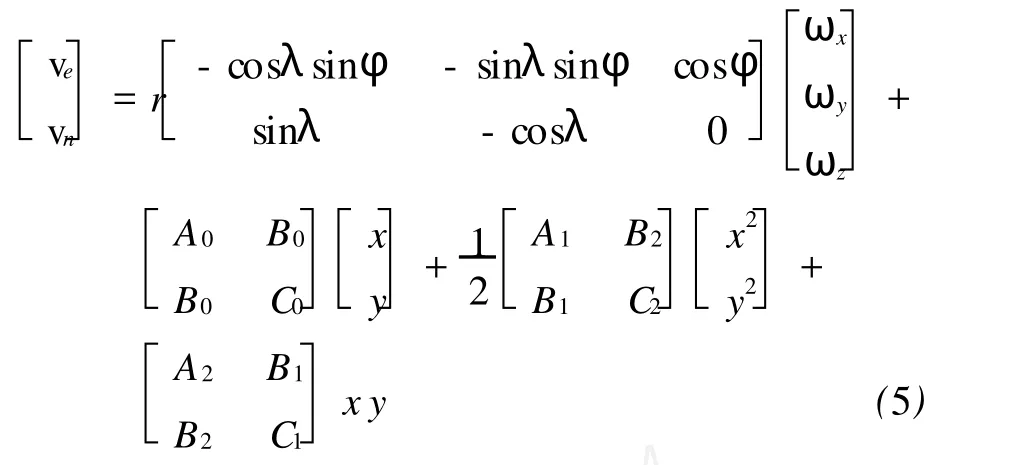
这里,x=rcosφ(λ-λ0);y=r(φ-φ0);(λ,φ)为点经纬度;(λ0,φ0)为几何中心经纬度;A0、A1、A2、B0、B1、B2、C0、C1、C2为应变参数。任一点的应变表示为

本文根据李延兴等提供的应变参数计算了青藏高原及周边2°×2°的应变场[19]。

对于地壳内部应变场,本文采用以下公式推算。Press提出在均质半空间内,由某点作用力产生的内部位移公式[20],表示为

这里,u表示由某点(ξ1,ξ2,ξ3)作用力 F在地壳内部某处(x1,x2,x3)产生的位移;α=(λ+μ)/(λ+ 2μ);R1=x1-ξ1;R2=x2-ξ2;R3=-x3-ξ3;R2=++。将式(7)用应变表示为

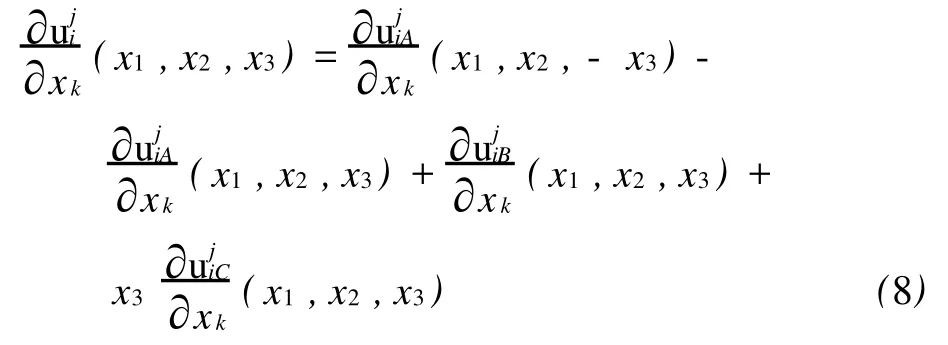
将式(6)简写为

根据胡克定律,弹性介质内应力与应变之间的关系表示为

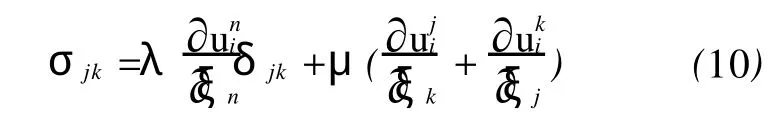
根据平衡方程

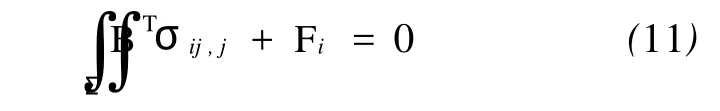
B是微分算子矩阵。根据式(9)、式(10)、式(11)可以得到均质半空间内,作用力 F引起的两点(x1,x2,x3)和(ξ1,ξ2,ξ3)应变关系为

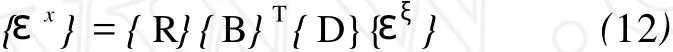
式(12)为本文推导的弹性均质半空间内(ξ1, ξ2,ξ3)点应变引起(x1,x2,x3)点应变公式。利用此式可以反演地壳脆性层内部的应变。

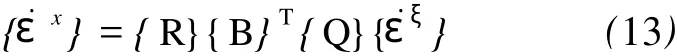
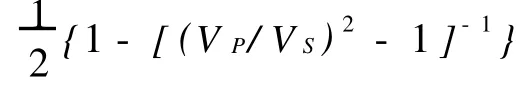
2.3 脆性-韧性转换面分布

得到温度场和应变率场后,利用式(4)就可以估算转换层深度h。计算结果见图2。

图2 青藏高原地壳脆性-韧性转换面Fig.2 Brittle-ductile transition plane of Tibetan plateau

从图中可以看出,地壳脆性-韧性转换面不是在固定深度,不同的区域其转换深度是有差异的。结果分析看,特点如下:①转换面一般位于中地壳,深度一般在22～37 km之间;②地壳厚度较大的区域,转换面深度也较深。原因是多方面的,这与温度变化、物质分布等因素有直接的关系。温度变化较慢,温度较低的区域,其转换深度就较深;反之,则较浅。

4 粘滞系数的分布

在确定了温度和应变率后,利用式(14)可以计算不同深度的等效粘滞系数。结果见图3。

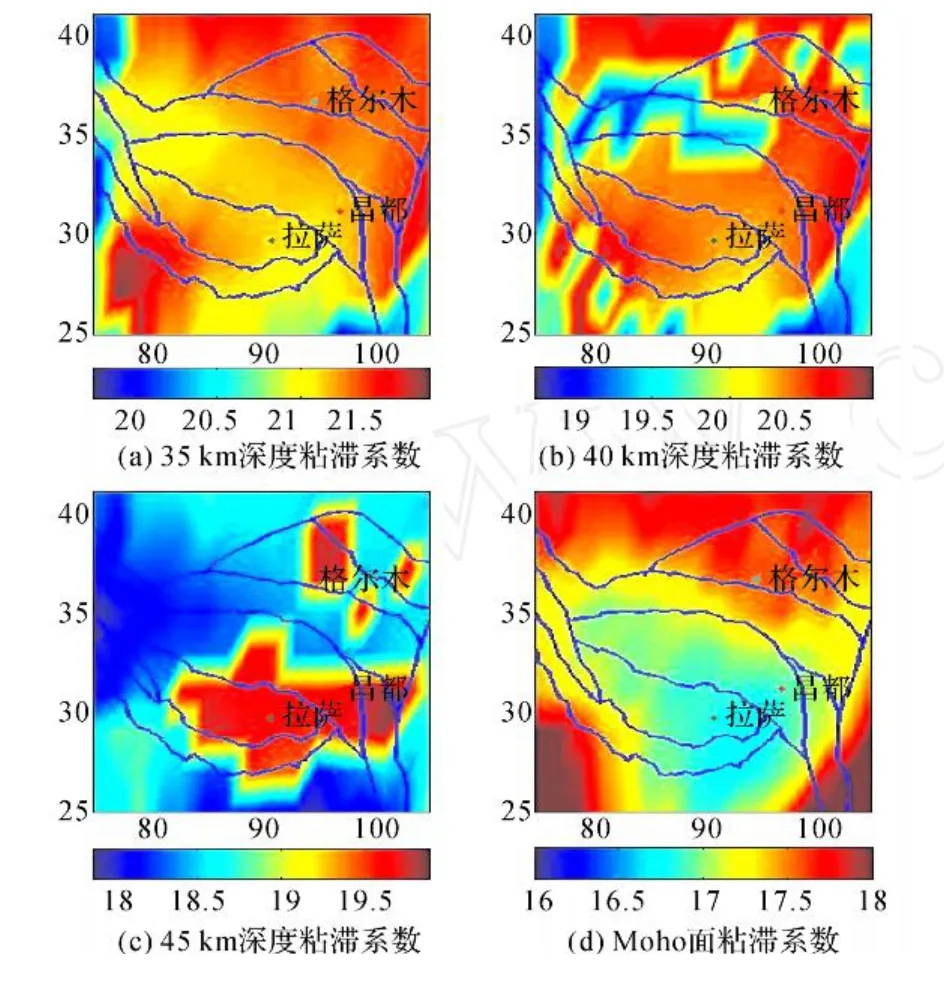
图3 青藏高原不同深度粘滞系数(用常用对数表示)Fig.3 Varied depths effective viscosity in Tibetan Plateau(expressed by common logarithm)

从图中可以看出,粘滞系数随深度的增加而呈下降趋势。大概平均深度每增加5 km,粘滞系数下降约0.5～1.0个数量级;在藏南等地壳较厚处,粘滞系数下降速率较慢,而地壳较薄处,粘滞系数下降较快。Moho面粘滞系数大约在1016～1018Pa·s之间,比转换面降低了大约3～5个数量级。

5 结 论

本文利用GPS计算的应变率、Crust2.0模型等、地表热流等数据,估算了青藏高原地壳内不同深度的温度场及地壳内脆性-韧性转换面的深度,推导了地壳内部作用力引起两点应变之间的关系公式,并计算了韧性层内不同深度等效粘滞系数的分布。结果表明:青藏高原及周边区域脆性-韧性转换面一般位于中地壳,深度分布在22～37 km之间,地壳较厚的区域转换面也较深;韧性层内粘滞系数分布,在中地壳约为1019～1022Pa·s之间,下地壳在1017～1020Pa·s之间,Moho面则降至1016～1018Pa·s。

其他学者也进行过等效粘滞系数的研究,张晁军等[9]分别利用流变定律及地震震后变形计算了青藏高原下地壳的粘滞系数,得到昆仑山地区下地壳粘滞系数为1017Pa·s[9],与本文得到的结论基本一致。石耀霖等利用流变定律计算的中国大陆地壳粘滞系数为[8],中地壳等效粘滞系数一般在1021～1024Pa·s,下地壳粘滞系数在1021～1022Pa·s,其中青藏高原因为地壳厚、温度高,下地壳等效粘滞系数为1019～1020Pa·s。与之相比,本文得到的粘滞系数相对较小,这与本文采用的应变率较大,且随着深度的增加而增加有关。

[1] TURCOTTE D L,SCHUBERT G.Geodynamics:Applications of Continuum Physics to Geological Problems[M]. New York:John Wiley,1982.

[2] ROYDEN L.Coupling and Decoupling of Crust and Mantle Inconvergent Orogens:Implications for Strain Partitioning in the Crust[J].Journal of Geophysical Research,1996, 101(8):17679-17705.

[3] CHEN W P,MOLNAR P.Focal Depths of Intracontinental and Intraplate Earthquake and Their Implication for the Therma and Mechanical Properties of the Lithosphere[J]. J Geo-phys Res,1983,88:4183-4214.

[4] SHIMADA M.Lithosphere Strength Inferred from Fracture Strength of Rocksat High Confining Pressuresand Temperatures[J].Tectonophysics,1993,217:55-64.

[5] ZANG Shaoxian,LI Chang,WEI Rongqiang.The Determination of Rheological Mechanics of Lithosphere and the Influencing Factors on the Rheological Strength of Lithosphere[J].Progress in Geophysics,2002,17(1):50-60. (臧绍先,李昶,魏荣强.岩石圈流变机制的确定及影响岩石圈流变强度的因素[J].地球物理学进展,2002,17(1): 50-60.)

[6] ZHANG Chaojun,CAO Jianling,SHI Yaolin.Studying the Viscosity of Low Crust ofQinghai-TibetPlateau According to Post-seismic Deformation[J].Sci China: Earth Sci,2008,38(10):1250-1257.(张晁军,曹建玲,石耀霖.从震后形变探讨青藏高原下地壳黏滞系数[J].中国科学:地球科学,2008,38(10):1250-1257.)

[7] HILLEY G E,BURGMANN R,ZHANG P Z,et al. Bayesian Inference of Plastosphere Viscosities Near the Kunlun Fault,Northern Tibet[J].Geophys Res Lett, 2005,32:1302-1305.

[8] WANG Wei,WANG Shengzu,CUI Xiaofeng.Strength Character of Granite of Juyongguan and Gabbro of Jinan Under Condition of Pressure and Temperature of Crust[C]∥Motion of Present Crust.Beijing:Earthquake Press, 1988:163-168.(王威,王绳祖,崔效锋.地壳温压条件下居庸关花岗岩、济南辉长岩的强度特性[C]∥现代地壳运动.北京:地震出版社,1988:163-168.)

[9] RUDNICK R L,FOUNTAIN D M.Nature and Composition of the Continental Crust:A Lower Crustal Perspective [J].Rev Geophys,1995,33(3):267-309.

[10] CARTER N L,TSENN M C.Flow Properties of Continental Lithosphere[J]. Tectonophysics,1987,136: 27-63.

[11] OHNAKA M.The Quantitative Effect of Hydrostatic Confining Pressure on the Compressive Strength of Crystalline Rock[J].J Phys Earth,1973,21:125-140.

[12] ZHAN Liu,WANG Shengzu,SHI Liangqi.Strength Character of Six Types of Rocks of China under High Pressure[J].Journal of Mechanics of Engineering of Rock,1985,4(1):10-19.(张流,王绳祖,施良骐.我国六种岩石在高围压下的强度特征[J].岩石力学与工程学报,1985,4(1):10-19.)

[13] WEI Rongqiang,ZANG Shaoxian.Effects of Temperature and Strain Rate on the Fracture Strength of Rock and Their Influences on the Rheological Structure of the Lithosphere[J].Chinese Journal of Geophysics,2006,49 (6):1730-1737.(魏荣强,臧绍先.岩石破裂强度的温度和应变率效应及其对岩石圈流变结构的影响[J].地球物理学报,2006,49(6):1730-1737.)

[14] WANG Y.Heat Flow Pattern and Lateral Variations of Lithosphere Strength in China Mainland:Constraints on Active Deformation[J].Phys Earth Planet Inter,2001, 126:121-146.

[15] WANG Yang,WANGJiyang,XIONG Liangping,et al. Lithosphere Geothermics of Major Geotectonic Units in China Mainland[J].Acta Geoscientica Sinica,2001,22 (1):17-22.(汪洋,汪集旸,熊亮萍,等.中国大陆主要地质构造单元岩石圈地热特征[J].地球学报,2001,22 (1):17-22.)

[16] AN Meijian,SHI Yaolin.Three-dimensional Thermal Structure of the Chinese Continental Crust and Upper Mantle[J].Sci China:Earth Sci,2007,50(10):1441-1451.(安美建,石耀霖.中国大陆地壳和上地幔三维温度场[J].中国科学:地球科学,2007,37(6):736-745.)

[17] LI Yanxing,HUANG Cheng,HU Xinkang,et al.The Rigid and Elastic-plastic Model of the Blocks in Intro-plate and Strain Status of Principal Blocks in the Continent of China[J].Acta Seismologica Sinica,2001,23(6):565-572.(李延兴,黄王成,胡新康,等.板内块体的刚性弹塑性运动模型与中国大陆主要块体的应变状态[J].地震学报,2001,23(6):565-572.)

[18] YANG Guohua,LI Yanxing,HAN Yueping,et al.Current Horizontal Strain Field in Chinese Mainland Derived from GPS Data[J].Acta Seismologica Sinica,2002,24(4): 337-347.(杨国华,李延兴,韩月萍,等.由 GPS观侧结果推导中国大陆现今水平应变场[J].地震学报,2002, 24(4):337-347.)

[19] LI Yanxing,LI Zhi,ZHANGJinghua,et al.Horizontal Strain Field in the Chinese Mainland and its Surrounding Areas[J].Chinese Journal of Geophysics,2004,47(2): 222-231.(李延兴,李智,张静华,等.中国大陆及周边地区的水平应变场[J].地球物理学报,2004,47(2): 222-231.)

[20] PRESS F.Displacement,Strain and Tilts at Tele-seismic Distances[J]. Journal of Geophysics, 1965, 70: 2395-2412.

[21] TENGJiwen.Introduction to Sold Geophysics[M].Beijing: Earthquake Press,2003.(滕吉文.固体地球物理学概论[M].北京:地震出版社,2003.)

[22] XIAO Lanxi.Study the Geodynamic Driving Mechanism of Continental Lithosphere in China by the India-Eurasia Collision[D].Beijing:Institute ofGeophysics,China Earthquake Administration,2003.(肖兰喜.中国大陆板内构造运动的动力学研究[D].北京:中国地震局地球物理研究所,2003.)

(责任编辑:丛树平)

A Research about Effective Viscosity of Tibetan Plateau Lithosphere Viscoelastic Ductile Layer Using GPS Velocity Fields

Y ANG Qiang1,2,DANG Yamin1,2,3
1.School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China;2.Institute of Geodesy and Geodynamic,Chinese Academy of Surveying and Mapping,Beijing 100039;3.Shandong University of Science and Technology,Qingdao 266510,China

Crust is divided into two layers:the elastic brittle layer and the viscoelastic ductile layer.Meanwhile,it is supposed that the elasticbrittle layer approximates to elasticity,and the viscoelasticductile layer is viscoelastic.Strain fields are calculated using GPS horizontal velocity,and a strain relation expression between two points is deduced.Meantime,interior temperature field of lithosphere is evaluated by steady heat conductive equation.Under the condition that fracture intensity is equal to creeping intensity,brittle-ductile transition plane is obtained.Varied depth effective viscosity of Tibetan plateau lithosphere are calculated.The results show that brittle-ductile transition plane generally locates in middle crust about 22～37 km depth.The thicker the crust,the deeper the transition floor.Effective viscosity of middle crust located in Tibetan plateau is between 1019～1022Pa·s, and lower crust is between 1017～1020Pa·s.It decreases to 1016～1018Pa·s at Moho plane.

GPS velocity fields;brittle-ductile transition plane;temperature field;strain rate;effective viscosity

Yang Qiang(1975—),male,PhD candidate,majors in geodynamics and satellite geodesy.

E-mail:sdyangqiang@163.com

1001-1595(2010)05-497-06

P227

A

国家863计划(2009AA121405,2009AA12Z318);国家自然科学基金(40974016)

2009-09-01

2010-05-07

杨强(1975-),男,博士生,研究方向为地球动力学,卫星大地测量。