Lagrange中值定理证明的几点注记

张长记

(河池学院 数学系,广西 宜州 546300)

Lagrange中值定理证明的几点注记

张长记

(河池学院 数学系,广西 宜州 546300)

证明 Lagrange中值定理的关键是构造一个满足 Rolle定理条件的辅助函数,用代数和几何的知识构造出几个辅助函数,从而注明了构造辅助函数的思想方法 .

Lagrange中值定理;辅助函数;变换;旋转;平移

0 引言

Lagrange中值定理:若函数f(x)满足下列条件:1)在闭区间[a,b]上连续;2)在开区间(a,b)内可导,则在开区间(a,b)内至少有一点c,使

证明这个定理的关键是构造一个满足 Rolle定理条件:φ(a)=φ(b)的辅助函数φ(x),在教科书中通常是直接给出一个函数

再验证函数φ(x)满足 Rolle定理条件:φ(b)=φ(a).缺少如何这样构造辅助函数的思想方法说明,读者看完后难免会想:“这方法是怎么想到和做到的?”

文献[2]中比较明确地介绍了“函数与直线差”的方法:

如图 1中,直线AB的方程为

1 主要结果

利用坐标变换和线性变换的思想构造出满足 Rolle

定理条件的辅助函数.以下列出几个满足 Rolle定理条件的辅助函数,并注明构造这几个辅助函数的思想方法的过程 .

1.1 平移加旋转坐标系的方法

1)先把坐标系原点平移到A点则有

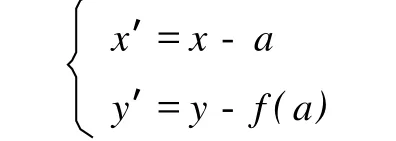
如图 2.此时AB所在的直线方程为

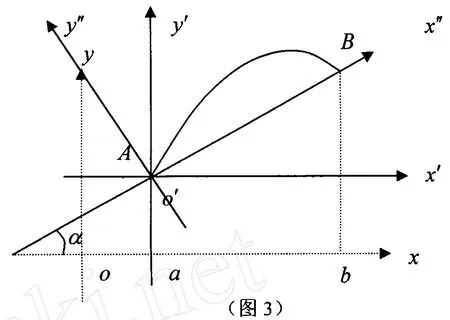
2)坐标系x′o′y′逆时针旋转 α角,如图 3,由坐标变换公式有

1.2 旋转坐标系的方法

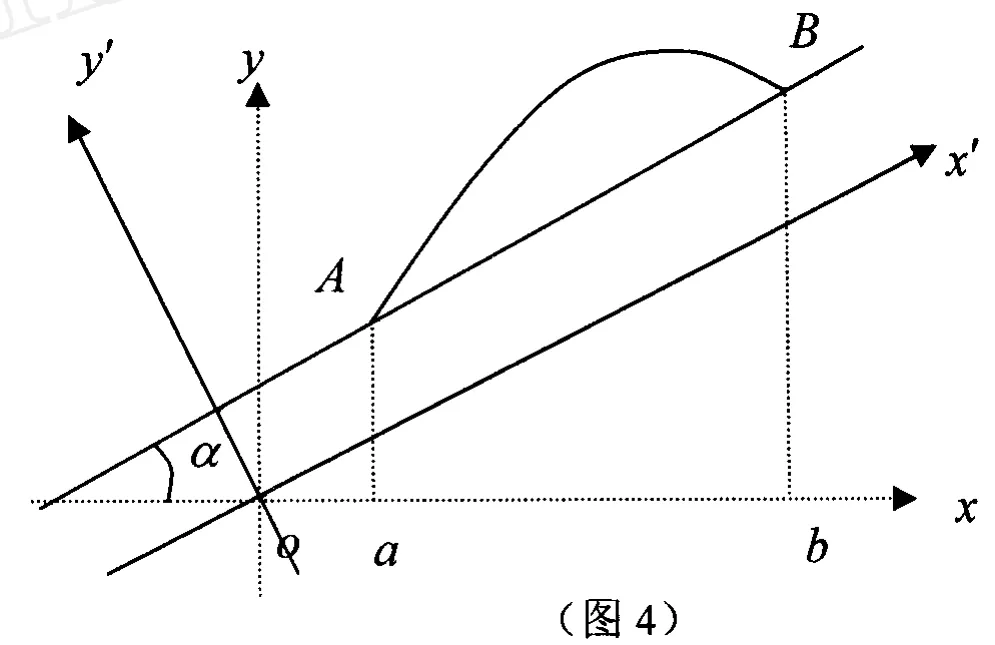
去掉 1.1中平移坐标系这一环节,直接把坐标系xoy逆时针旋转α角,如图 4.由坐标旋转公式:

从而φ(x)满足 Rolle定理条件:φ(a)=φ(b).

1.3 平移加旋转函数的图象的方法

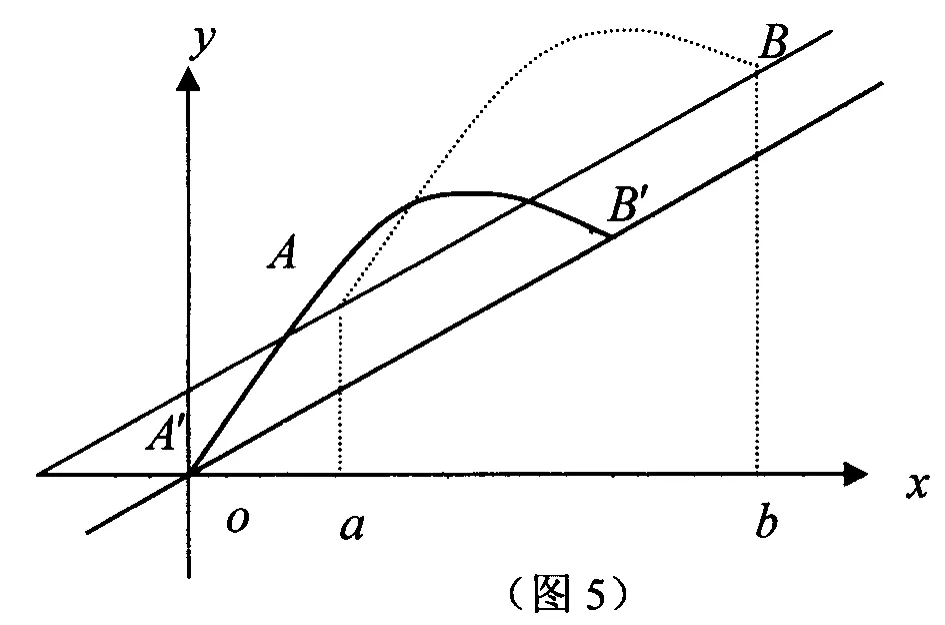
1)把函数图象平移到A点与坐标原点O重合,如图 5.即作变换

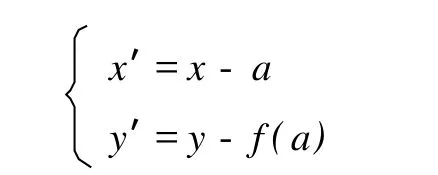
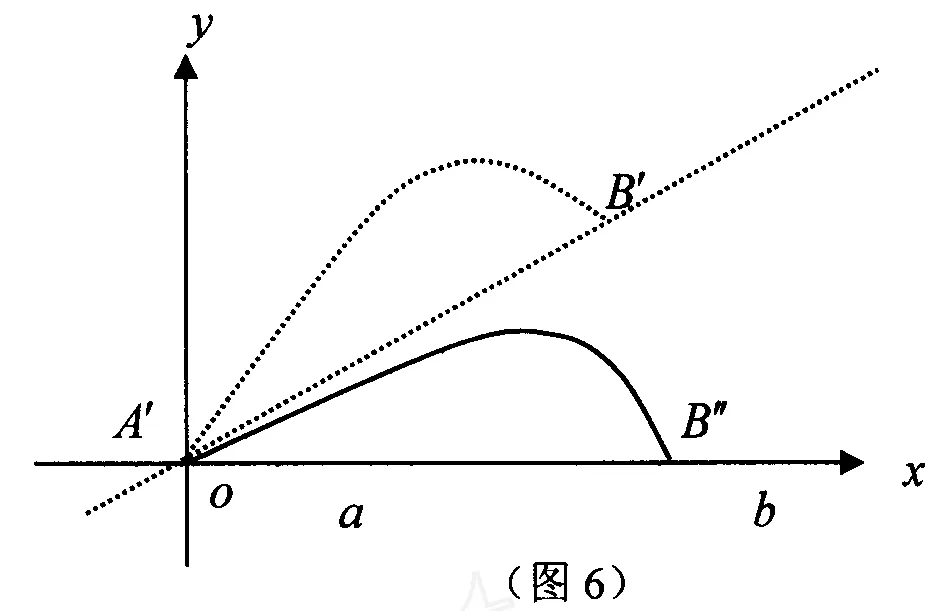
2)把平移后的图象再顺时针旋转α角,如图 6,即作变换

综合 1)和 2),进行运算,方法同 1.1,其结果也和 1.1相同 .

1.4 旋转函数的图象的方法

省去 1.3中的 1),直接把y=f(x)的图象以坐标原点o为中心顺时针旋转α角,如图 7即作线性变换

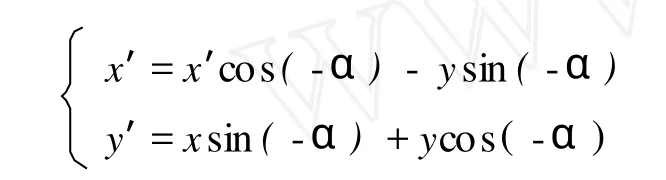
后进行计算,计算方法和所得结果与 1.2的相同.

以上 4种方法尽管计算方法、过程和结果都十分相近,乃至相同,但是却反映了 4种不同的思想方法.由于这些方法都很直观,结论也优美,用到教学上可解决一些直观问题,体现学科之间的交错互用问题,对学生渗透变换和相对运动的思想,发展学生的思维能力和培养学生的创新能力应该有一定作用.

[1]刘玉琏,傅沛仁.数学分析讲义 (上册)[M].北京:高等教育出版社,1990.

[2]同济大学应用数学系.高等数学 (第五版)[M].北京:高等教育出版社,2003.

[3]孟道骥.高等代数与解析几何[M].北京:科学出版社,2002.

Several Remarks on Proving theM ean Valve Theorem of Lagrange

ZHANG Chang-ji

(Department ofMathematics,Hechi Un iversity,Y izhou,Guangxi546300,Ch ina)

Constructing auxiliary function to meet the condition of Rolle Theorem is very important in proving the mean valve theorem of Lagrange.This paper gives several methods and thoughts of constructing auxiliary functions.

the mean valve theorem of Lagrange;auxiliary function;transfor mation;revolution;paralleltranslation

O171

A

1672-9021(2010)02-0012-03

张长记 (1954-),男,广西象州人,河池学院数学系副教授,主要研究方向:代数学及其教学 .

2010-03-28

[责任编辑普梅笑 ]