含左手材料的光子晶体
2010-12-22姜友嫦
许 刚 姜友嫦
(重庆三峡学院物理与电子工程学院,重庆万州 404100)
光子晶体是在1987年首先由Yablonovitch[1]和John[2]分别提出的,它是由不同折射率的介质周期性排列而成的人工微结构.介电常数的周期性变化使得光子晶体产生类似于固体电子能带结构的光子带隙结构(photonic band gap).在一定的频率范围内,电磁波在光子晶体内将不能发生任何方向的传播,即所谓的“光子禁带”.光子晶体在光纤、微波通讯和滤波器等方面大有用途.近年来,由于左手人工介质的出现以及与之相关的负折射现象激发了科学家对光子晶体的新一轮研究热潮.1968年,前苏联科学家Veselago从理论上虚构了一种介电常数和磁导率均为负数的材料.在这类物质中,电磁波的电场矢量、磁场矢量和波矢服从左手定则,故称“左手材料”,或“双负材料”.介电常数和磁导率同时为负,并不违反电磁场Maxwell方程和物质本构方程.在左手材料中,电磁波的群速度和相速度方向相反,导致左手材料中存在负折射效应、反常Cherenkov效应和反常Doppler材料[3]效应等一系列与人们熟悉的现象相反的奇特效应.
1 介电常数、磁导率与折射率
介电常数ε及磁导率μ是用于描述物质电磁性质的两个基本物理量,决定着电磁波在物质中的传播特性.一般情况下,介电常数和磁导率都是频率和空间的复函数,对于吸收媒质,它们分别可以表示成指数形式:
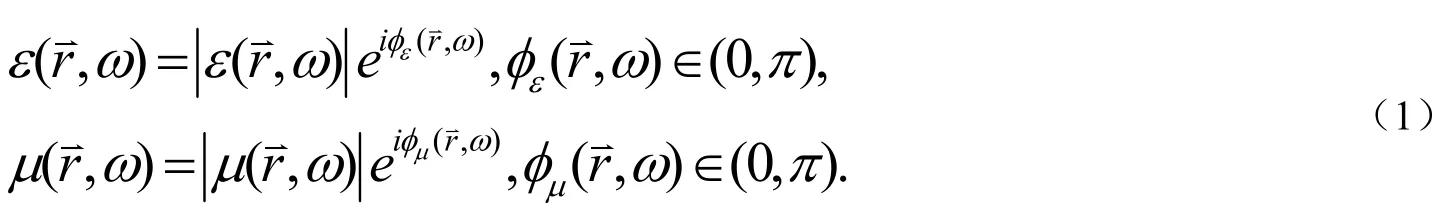
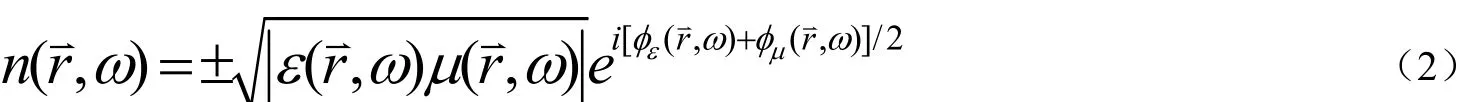
其中




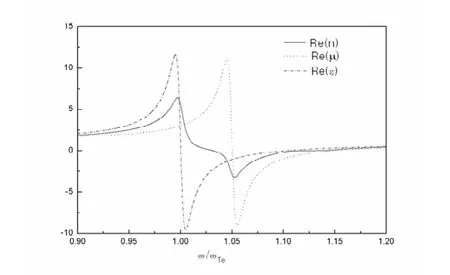
图1 折射率实部、介电常数实部和磁导率实部与频率的关系

图2 折射率虚部、介电常数虚部和磁导率虚部与频率的关系
2 左手介质的电磁学性质
根据复数形式的Maxwell方程组和介质的本构关系,正弦时变电磁波的波动方程,即 Helmholtz方程为[4]

其中: k2=ω2με,对于μ和ε都为正数的介质,方程(1)有波动解,电磁波能在其中传播.对于无损耗,各向同性,空间均匀的介质,由Maxwell方程可得:[5]

3 电磁波在左手介质中的传播速度
3.1 相速度
在左手介质中,按照波动理论,波速的数值由下列方程决定:


3.2 群速度
在左手介质中传播的高斯波或微波都可以看成是由众多不同频率、不同振幅的单色正弦波或余弦波叠加而成的,即可将任何波写成傅里叶级数或傅里叶积分的形式.在无色散介质(如真空)中所有这些组成波的单色平面波都以同一速度传播,那么该波在传播过程中将永远保持形状不变,整个波也永远以这一速度向前传播.但是除真空以外,任何介质通常都具有色散的特征,也就是说,各个单色平面波各以不同的相速传播,其大小随频率而变,所以由它们叠加而成的波在传播过程中将不断改变其形状.

下面讨论瑞利公式为何不适用于左手介质.

②当 0<n< 1时,若介质是色散性质的,即
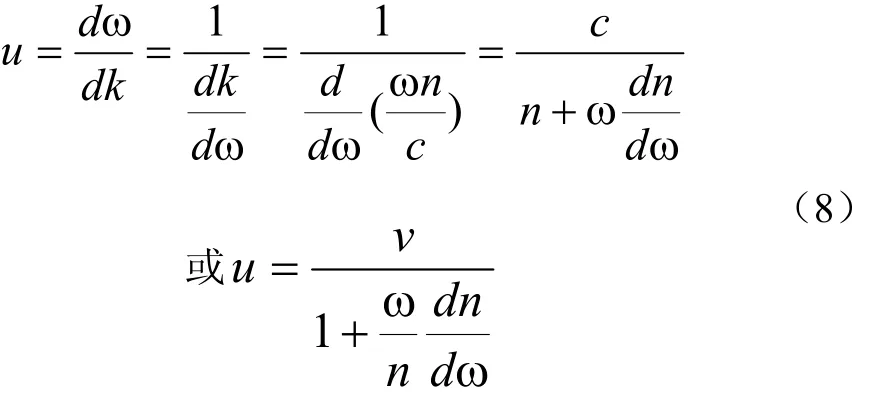


4 结 论
[1]E.Yablonovitch, Phys.Rev.Lett. 58 (1987) 2059.
[2]S.John, Phys.Rev.Lett.58(1987)2486.
[3]陈龙,何赛灵,沈林方.含负折射率介质的多层结构中倏逝波传播及隧道效应的分析[J].物理学报,2003(52):2386-2392.
[4]郭硕鸿.电动力学[M],北京:高等教育出版社,2007.
[5]粱灿彬.电磁学[M].北京:高等教育出版社,2007.
