NaRb分子的a3∑+电子态完全振动能级和离解能的研究

2010-12-22舒纯军王安蓉孙卫国

重庆三峡学院学报 2010年3期

舒纯军王安蓉孙卫国

(1.重庆三峡学院物理与电子工程学院，重庆万州 404100)

（2.西华大学，四川成都 610065)

和原子光谱一样，分子光谱是人们认识微观世界的重要工具和手段.通过对分子光谱的研究，可以得到分子中电子的运动、原子核的振动与转动的详细信息，同时还能证明以前在化学中不知道的或被认为不能自由存在的分子状态的存在.此外，材料加工、分析测量技术、激光技术的发展，都与光谱理论有着密切的联系.[1][2][3]

近几十年来，虽然人们对很多双原子分子体系中的原子核运动做了大量的研究，但由于很多分子的高振动激发态的光谱比较复杂，对光谱仪器的分辨率要求较高；同时，分子中存在对分子振动和转动运动影响很大的各种物理作用：电子-电子、电子-核、核-核相互作用，轨道-自旋耦合，核磁矩，相对论效应等，使得用实验方法精确测定或量子理论方法精确计算这些高振动激发能级的光谱变得非常困难.[2][3][4]

本文用孙卫国等建立的研究双原子分子精确振动能级的代数方法（AM），研究了碱金属异核双原子分子NaRb的a3∑+电子态的完全振动能谱，并使用基于AM的代数能量方法（AEM）研究了该电子态的分子离解能De，均得到了满意的结果.本文第二部分介绍理论方法，第三部分应用AM方法和AEM方法具体研究了NaRb分子的a3∑+电子态的完全振动能级和离解能，第四部分对本文进行总结.

1 代数能量方法(AEM)

孙卫国等用二阶微扰理论获得了双原子分子电子态的非相对论核运动的振转能级的高阶展开表达式，[5][6]当忽略转动运动时，其表达式变为：

将此理论能级解析式与Herzberg的振动能级经验公式[1]对比可知，该式中ω0和ωe0是新出现的项.ω0对应于(υ+1/2)的第零阶振动光谱常数，与Dunham能量表达式[7]的Y00项一致；ωe0是(υ+1/2)的第一阶谐振光谱常数ωe的修正项.ω0和ωe0虽然都是小量，但是它们在计算振转能级 Eυj时是很重要的.[5]代数方法（AM）[5]的基本思路如下.将根据微扰理论获得的振动能级公式(1)改写成矩阵形式：

其中，振动光谱常数的向量矩阵X和振动能量矩阵E分别为：

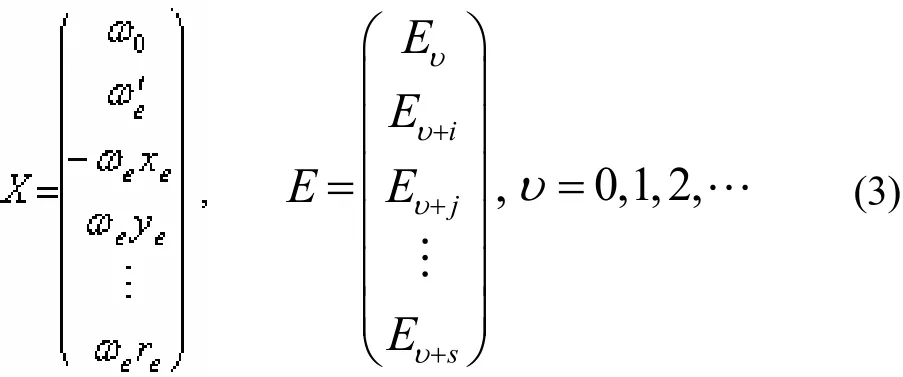
上式中，ωe′=ωe+ωe0.(2)式中的A是n×8阶的系数矩阵，其矩阵元的形式为 A=(υ+1/2)k，k=0,1,2,…,7.

对于大多数双原子分子的电子态，现代实验技术总能获得该电子态完全振动能谱{Eυ}中的一部分量子态不太高的m个振动能级的精确数据.人们可从这m个实验能级组成的能级子集合[Eυ]中选取N(=)个小能级组，每组8个能级，解方程(2)N次，可以得到N组振动光谱常数Xs′.在这N组常数中，总有一组振动光谱常数X能同时最好地满足下列要求：

为了获得分子离解能的正确数值，孙卫国和任维义等在AM振动能谱的基础上建议了代数能量方法(AEM).[8][9]AEM提出的分子离解能的上、下界如下：

或

(8)式右边的求和等价于分子最高振动能级υmax上所有物理上存在的转动能级之和.对于很多双原子分子电子态，该求和项非常小，或者为零，则(8)式变为：

即这些电子态的真实离解能De等于或非常接近于(8)式中的下界 Eυmax.对于那些势阱很浅或不太稳定的双原子分子电子激发态，要得到该电子态离解能的精确数值还很困难，因而有时文献上还缺乏这些态的离解能数据.根据我们的经验，在(10)成立的条件下，由下式：[8][9]

以上基于AM精确振动能谱和利用离解能上下界的性质来获得分子离解能 De的方法称为代数能量方法（AEM-algebraic energy method）.

2 AEM方法对NaRb分子的a3∑+电子态应用及讨论

本文首次用AM方法和AEM方法研究了碱金属异核双原子分子NaRb的a3∑+电子态，并将得到的振动光谱常数、完全振动能谱、最高振动能级和分子离解能与文献值进行了对比分析，其结果分别列于附表1、附表2和附表3中.

附表1给出了NaRb分子的a3∑+电子态的振动光谱常数(ω0,ωe0,ωe,ωeχe,ωeye,ωeze,ωete,ωese, ωere)、最大振动量子数υmax、最高振动能量 Eυmax和离解能De.从附表1中可以看到，由AM方法得到的谐振常数ωe与该电子态的文献值吻合得非常好；但文献还比较缺乏高阶振动光谱常数的数据.

从附表2列出的NaRb分子的a3∑+电子态的AM完全振动能谱{Eυ}可以看到，AM振动能谱不仅与已知的实验能级或 Rydberg-Klein-Rees (RKR)数据很好地重合，而且获得了用现代实验方法或精确的量子理论方法很难得到的所有高振动激发态的能级，进而得到了非常接近于离解极限的最高振动能级和最大振动量子数υ .max

3 结论

对于大多数双原子分子的电子态，目前文献上还比较缺乏高振动激发态的能级数据，这主要是由于处于高振动激发态的分子振动太快且常不稳定，各种微观量子效应错综复杂，要从实验上测量或用量子理论计算这些体系所有的高振动激发能级往往非常困难.本文应用孙卫国等建立的 AM[5]方法和AEM[8][9]方法，研究了碱金属异核双原子分子NaRb的a3∑+电子态的完全振动能谱和分子离解能De，得到了比较满意的结果.与其他量子理论计算方法相比，AM方法不仅计算过程简便，而且其结果严格忠实于客观规律.随着实验测量技术的不断进步，总可以从实验上获得一个稳定电子态的一组量子数不太高的振动能级的精确数据，这些能级包含了物理上所有重要的微观量子效应和分子振动信息.AM方法紧紧抓住这个客观事实，不使用任何物理模型和数学近似，根据经微扰理论证明了的振动能级与各振动光谱常数之间的客观函数关系（即公式（1）），采用数学方法严格求解该振动能级的代数方程组，进而得到了这些电子态的完全振动能谱{Eυ}.这些AM振动能谱，不仅与相应电子态的实验能级非常吻合，而且正确地得到了实验上还无法获得的所有高振动激发态的能级（见附表2）.使用基于AM完全振动能谱{Eυ}的AEM方法，获得了该电子态的 AEM离解能，其结果与实验离解能也符合得很好（见附表3）.

综上所述，用AM方法和AEM方法研究双原子分子的振动能谱和分子离解能所获得的结果优于目前很多量子理论计算方法所产生的数据；同时与现代实验方法测量双原子分子体系精确的完全振动能谱和离解能相比，AM方法和AEM方法更为简便、经济，是一种行之有效的方法.

附表：

表1 NaRb分子a3∑+电子态的振动光谱常数、最大振动量子数υmax、最高振动能级 Eυmax 和分子离解能De[所有量（υmax除外）均以cm-1为单位]

表2 NaRb分子 a3∑+电子态的实验振动能级和AM振动能谱（能量单位：cm-1）

表 3 NaRb分子 a3∑+分子电子态的 AEM离解能DeAEM 、离解能的近似值Deap、最大振动能量 Eυmax 与实验离解能的百分误差 # （能量单位：cm-1）

[1]Herzberg G. Molecular Spectra and Molecular Structure (I), Spectra of Diatomic Molecules. (New York: Van Nostrand),1953:1-92.

[2]徐克尊.高等原子分子物理学[M].北京：科学出版社，2000：4-20.

[3]物理学评述委员会.原子、分子和光学[M].伍烈尧，陈凌冰译.北京：科学出版社，1993:141-155.

[4]Levine R D and Bernstein R B. Molecular reaction dynamics[M].陶愉生译.北京：科学出版社，1986.

[5]Sun W G，Hou S L，Feng H and Ren W Y. Studies on the Vibrational and Rovibrational Energies and Vibrational Force Constants of Diatomic Molecular States Using Algebraic and Variational Methods[J].J. Mol. Spectrosc, 2002(215):93-105.

[6]Sun W G and Feng H. An energy-consistent method for potential energy curves of diatomic molecules [J].J. Phys. B: At. Mol. Opt. Phys.，1999(32)：5109.

[7]Dunham J L. The Energy Levels of a Rotating Vibrator [J]. Phys. Rev.，1932(41)：721-731.

[8]任维义，孙卫国.Na2分子部分电子态的完全振动能谱和离解能的精确研究[J].物理学报，2005（54）：594-605.

[9]Sun W G, Ren W Y, Hou S L and Feng H. Studies on full vibrational spectra and dissociation energies of some diatomic molecular electronic states using algebraic approaches. Molec. Phys.，2005，103：2335-2345.

[10]Zemke W T and Stwalley W C. Long-range potential energy curves for the X1Σ+ and a3Σ+ states of NaRb[J].J. Chem. Phys.，2001(114)：10811-10815.

[11]Wang Y C，Kajitani M，Kasahara S，Baba M，Ishikawa K and Katô H. High resolution laser spectroscopy of the B 1Π-X 1Σ+ transition of 23Na85Rb[J].J. Chem. Phys.，1991，95：6229-6237.