藕节形大深度潜水器耐压壳体强度与稳定性研究
2010-12-13陈爱志陈小宁刘土光
伍 莉,陈爱志,陈小宁,张 涛,刘土光,刘 均
(1武汉市第二船舶设计研究所,武汉430064;2华中科技大学交通学院船海系,武汉430074;3海军驻431厂代表室,辽宁 葫芦岛125004)
1 引 言
耐压壳体的强度和稳定性性能是大深度潜水器研究的关键,近年来引起了国内外各学者的关注。
关于大深度潜水器耐压壳体的研究大多集中在球形和圆柱形结构上。远藤伦正[1]率先对Ti-4-V-6钛合金材料球形大深度耐压壳体模型的稳定性进行了试验研究。陆蓓[2],李良碧[3]采用有限元法,分析了球形潜水器耐压壳体的临界压力与几何参数之间的影响曲线。王仁华[4]采用有限元法,研究了几何缺陷对球壳结构的稳定性影响。Liang Cho-Chung[5]研究了材料、重量排水量之比对深球形和椭球形潜器耐压壳体稳定性的影响。刘涛[6]考虑材料非弹性影响,给出了圆柱形潜水器耐压壳体稳定性的简易公式。对于耐压壳体的结构形式,从重量—排水量比的角度来看,球形最佳,而圆柱形有较高的空间利用率,综合两者的优点,新近出现了如图1所示的藕节形耐压壳体这种新的结构形式。Liang Cho-Chung[7]采用EIPF(extended interior penalty)和DFP(Davidon-Fletcher-Powell)方法,研究了多球壳连接的大深度潜水器耐压壳体的优化设计问题。为了改善图1中球壳直接相连导致的强度和稳定性问题,伍莉[8-9]提出了如图2所示的切弧连接这种新型的藕节形耐压壳体结构形式,并研究了考虑该结构形式的强度、稳定性以及几何约束等的优化设计。


本文采用有限元方法,研究了一系列几何参数下,大深度潜水器的三藕节切弧连接耐压壳体的强度和稳定性性能,提出该结构的材料线性和材料非线性强度经验公式;并考虑材料非线性的初始缺陷的影响,提出其稳定性经验公式。
2 耐压壳体的几何参数
本文研究的三藕节大深度潜水器耐压壳体的几何模型如图2,假定耐压壳体均匀等厚。R是球壳半径,t是耐压壳体的厚度,L是球壳中心间距,θ是连接角。在对其进行强度和稳定性分析时,将几何参数进行无因次化,记几何参数为。其中,tR是厚度半径比t/R,LR是球壳间距半径比L/R。选定几何参数范围:0.05%≤tR≤0.09%,1.9≤LR≤2.7,40°≤θ≤65°。
3 耐压壳体强度计算式的建立
3.1 线性材料的耐压壳体强度公式
若材料为线性,三藕节耐压壳体的强度只与外压力P0,以及几何参数(tR,LR,sin(θ))有关。参考球壳和圆柱壳的强度公式可知,外压力和几何参数是相互独立的参量,可以将耐压壳体的最大应力用如下公式表示:

式中的两个函数表达式均采用有限元方法来确定,有限元计算选取商业软件ANSYS进行几何非线性分析。由于耐压壳体为轴对称,属于厚壳范围,综合考虑计算精度和计算效率,有限元计算中选用轴对称实体单元PLAN_42,材料参数选用文献[1]中Ti-4-V-6钛合金线性模型:E=1.127e5MPa、ν=0.3,耐压壳体模型半径R=2 000mm。通过系列计算以及收敛性检验,确定网格大小为t/4×t/4,固定载荷增量步长为0.05。
3.2 F(P0)的确定
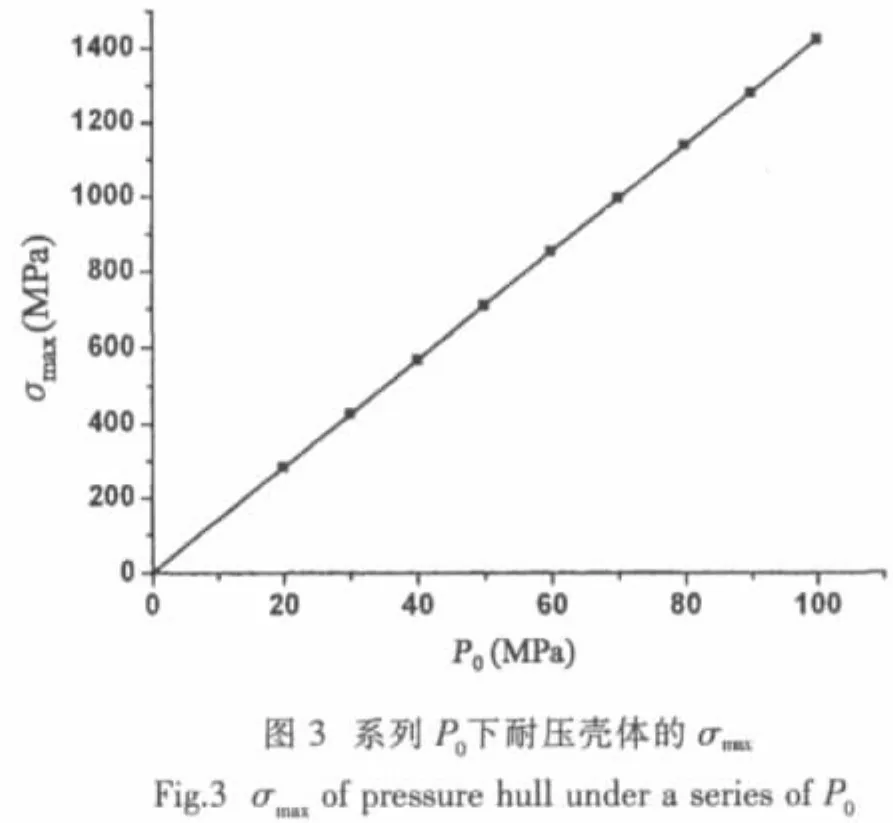
确定F(P0)时,假定几何参数(tR,LR,sin(θ))为定值,单独考虑σmax与P0之间的函数关系。 选定模型R=2 000mm,t=140mm,L=4 600mm,θ=55°。系列外压力P0下,耐压壳体的最大应力值列于表1和图3。从表1的记录结果和图3的曲线拟合可以看出,σmax是关于P0的一次函数,且对应拟合直线经过原点。本文选取:


表1 系列P0下耐压壳体的σmaxTab.1 σmaxof pressure hull under a series of P0
3.3 f1(tR)的确定
在确定σmax与(tR,LR,sin(θ))之间的函数关系时,假定P0为定值,选取P0=60MPa。
为了寻求tR与LR、sin(θ)之间的相关性,分别计算了LR、θ取以下五组典型数值时:(LR=2.3,θ=55°),(LR=2.3,θ=40°),(LR=2.3,θ=65°),(LR=1.9,θ=55°),(LR=2.7,θ=55°),系列tR下耐压壳体的最大应力值 σmax,见表2。图4给出了五组典型(LR,θ)下随厚度半径比tR的变化规律。其中是对应的耐压壳体的最大应力值,σ7max是对应的耐压壳体的最大应力值。

表2 系列厚度下耐压壳体的最大应力值Tab.2 σmaxof pressure hulls for a series of thick
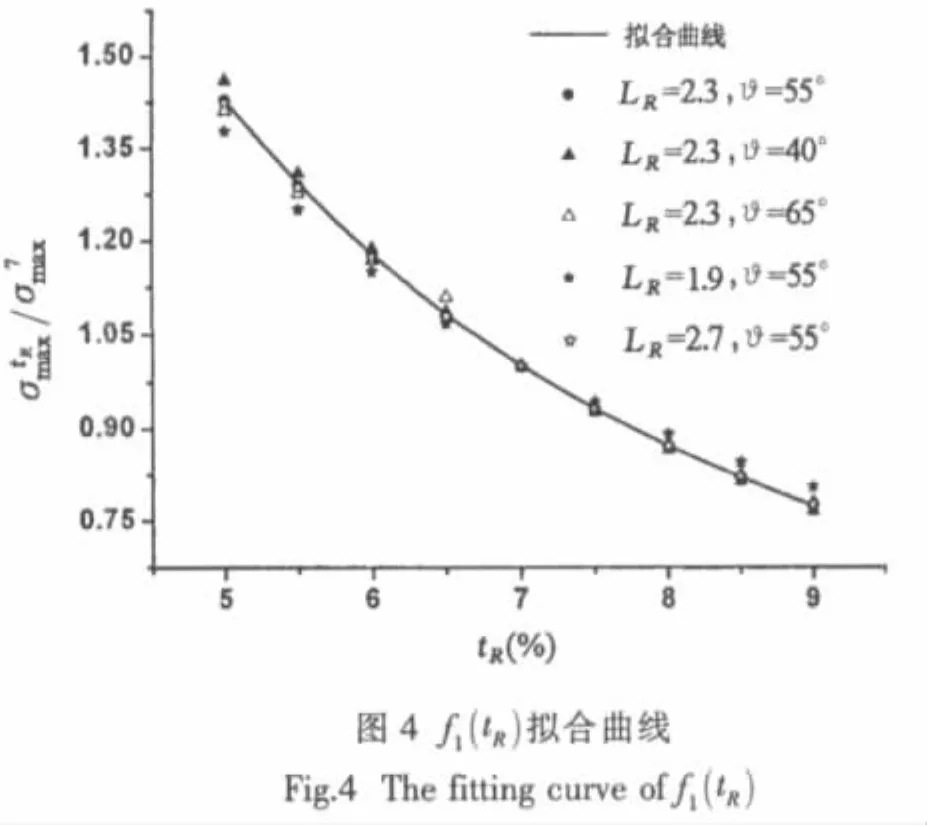
从图4可以看出五组典型(LR,θ)数值下,耐压壳体的σmax随tR的变化规律趋于一致,和LR、θ取中间值(LR=2.3,θ=55°)时的耐压壳体相比,误差小于3%,近似认为tR是与LR、sin(θ)无关的独立参量,因此(1)式可以写为如下形式:


其中,a1=-10.1,a2=16.25,a3=-0.088。大部分离散点的拟合误差在1%以内,最大误差不超过2.7%,可将tR视为与LR、sin(θ)无关的独立参量。f1(tR)的拟合曲线见图4。
3.4 f2(LR,sin(θ))的确定
假定外压力P0和耐压壳体的厚度半径比tR为定值:P0=60MPa,tR=7%,通过系列有限元计算进一步确定f2(LR,sin(θ))。
将P0和f1(7%)的取值代入(3)式得到:

其中σmax的单位为MPa。
系列球壳间距半径比LR、连接角θ下耐压壳体的最大应力值列于表3,联合表3和(5)式求得函数f2(LR,sin(θ)),并分别间隔选取几组典型离散点,其结果如图5、图6所示。通过反复尝试和误差比较,图5中的各组离散点采用四次多项式进行函数拟合可以获得较高的精度,图6则用线性拟合即可满足精度要求。因此本文假定f2(LR,sin(θ))的函数表达式如下:
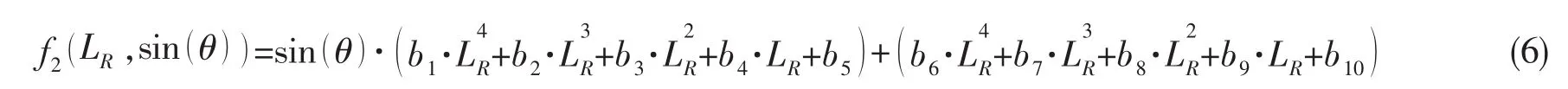

表3 系列LR、θ下耐压壳体的σmax(MPa)Tab.3 σmax(MPa)of pressure hulls for a series of LRand θ

表4 {bk}中各元素数值Tab.4 The value of{bk}

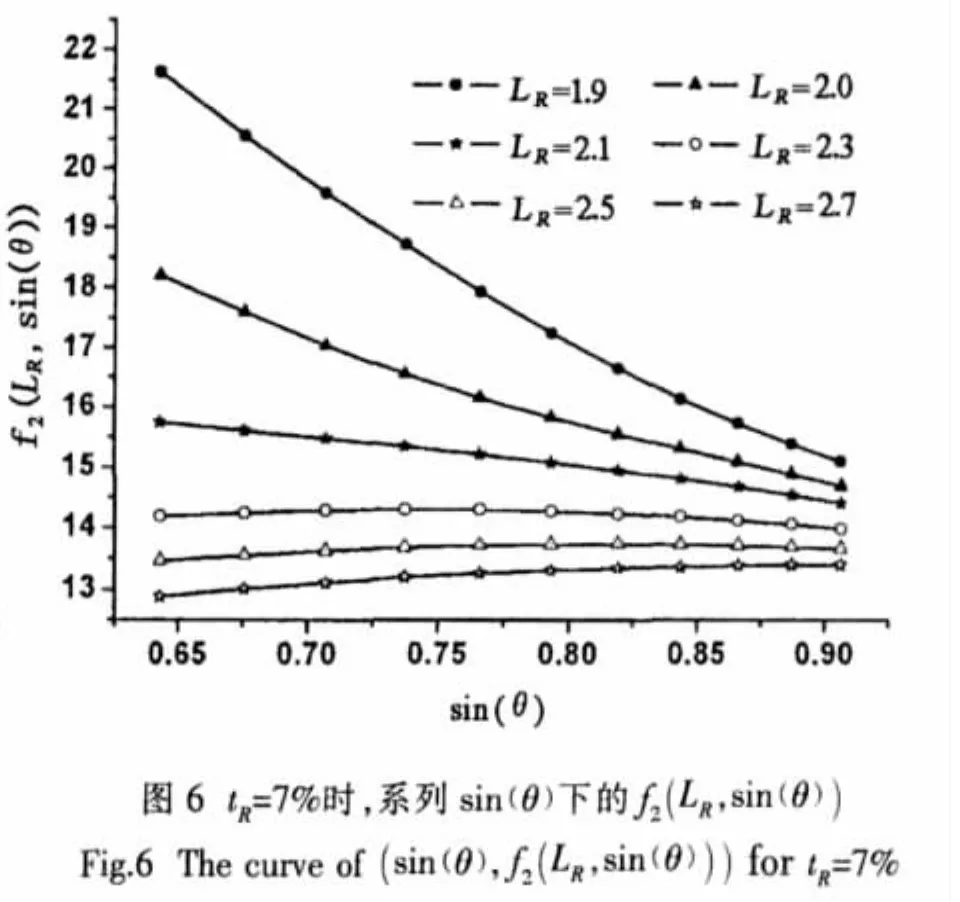
(6)式的拟合误差列于表5,从误差表中可以看出,大部分数值拟合误差都在1%以下,最大误差仅为-2.63%~1.15%,用(6)式来拟合f2(LR,sin(θ))具有足够高的精度。
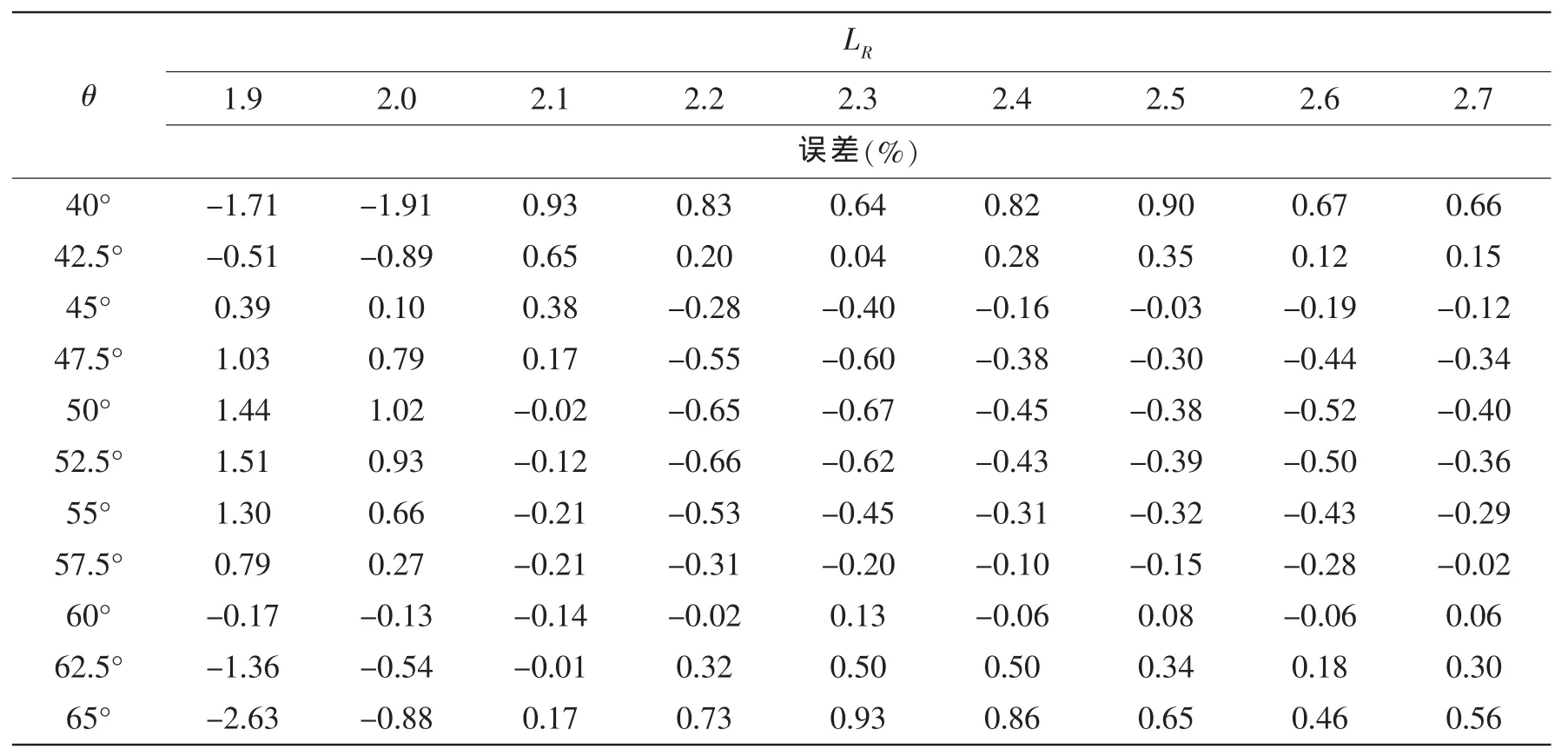
表5 f2(LR,sin(θ))的误差Tab.5 The error of f2(LR,sin(θ))
因此(3)式即为线性材料的三藕节切弧连接耐压壳体强度公式,其中的f1(tR)、f2(LR,sin(θ))分别由(4)式和(6)式求得。
3.5 非线性材料的耐压壳体强度公式
(3)式是不考虑材料非线性影响的三藕节切弧连接耐压壳体的强度公式,本文通过将非线性材料的应力—应变曲线引入(3)式得到非线性材料的耐压壳体强度公式。如图7所示,线性材料的应力—应变关系为:

非线性材料的应力—应变关系拟合为函数:

将(7)式中的ε代入(8)式即可得到非线性材料耐压壳体的强度公式:

其中 σmax由(3)式确定。
以大深度潜水器耐压壳体常用材料Ti-4-V-6钛合金为例,图8为文献[1]提供的应力—应变曲线,其主要材料参数为:杨氏模量E=1.127e5MPa,泊松比ν=0.3,屈服极限σs=872MPa。本文对其进行曲线拟合,得到应力—应变函数关系如下:

将(7)式代入应力—应变关系式(10)即可得到Ti-4-V-6钛合金三藕节切弧连接耐压壳体的强度公式:

式中,σmax由(3)式计算得到。

4 耐压壳体的稳定性计算式的建立
4.1 Ti-4-V-6钛合金耐压壳体的稳定性公式
本文考虑初始缺陷和材料非线性的影响,采用有限元法确定Ti-4-V-6钛合金耐压壳体的稳定性公式。
耐压壳体的稳定性与初始缺陷因子fR(fR=f/R,其中f是最大初始几何缺陷幅值),材料参数E、ν,以及几何参数(tR,LR,sin(θ))有关。假定材料与几何参数是无关参量,初始缺陷以缺陷项乘子引入,参考球壳和圆柱壳的稳定性公式,Ti-4-V-6钛合金三藕节切弧连接耐压壳体的临界失稳压力可以用如下公式来表示:

式中函数表达式F′(fR)和f′(tR,LR,sin(θ))均采用有限元法计算确定。 有限元计算选取商业软件ABAQUS进行非线性分析。为了确保计算的精确性,在非线性分析过程中分两个载荷步进行:第一个载荷步中,固定步长使用一般非线性屈曲分析,直至约为特征值屈曲临界载荷的80%;第二个载荷步中,固定弧长,使用弧长法使分析通过临界载荷。
为了反映潜水器耐压壳体的真实失稳过程,本文选用整体模型,模型单元采用适合于厚壳非线性分析的壳单元S8R。材料模型选用文献[1]提供的Ti-4-V-6钛合金非线性材料,参见图8,模型半径R=2 000mm。通过系列计算以及收敛性检验,确定网格大小为300mm×300mm,step1的固定增量步长为0.05,step2的固定增量步长为0.005。
4.2 缺陷项F′(fR)的确定
目前针对球壳初始缺陷的研究主要包含局部缺陷,和整体特征值屈曲模态缺陷,文献[4]的研究结果表明整体特征值屈曲模态缺陷形式对结构最为不利,本文中引入的缺陷项F(fR)主要是考虑这种对结构最为不利的缺陷形式。其中缺陷项表达式采用有限元法确定。
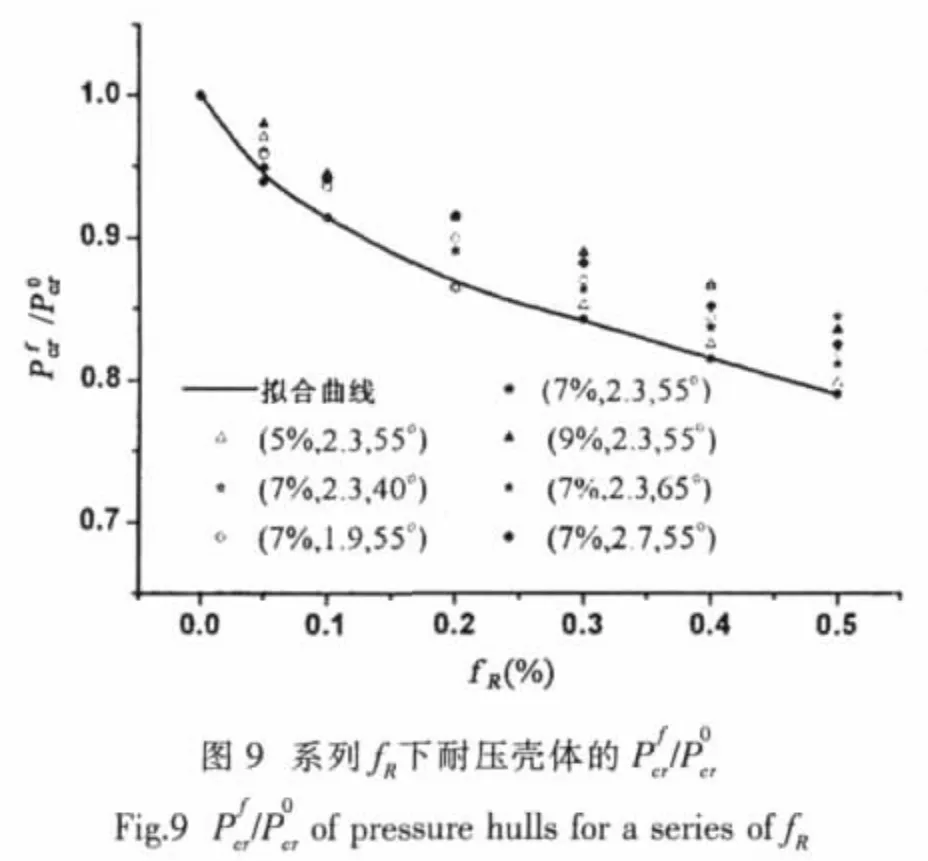
为了合理确定F′(fR),分别计算了七组典型(tR,LR,θ)数值的耐压壳体模型:(7%,2.3,55°),(5%,2.3,55°),(9%,2.3,55°),(7%,1.9,55°),(7%,2.7,55°),(7%,2.3,40°),(7%,2.3,65°),各fR耐压壳体的临界失稳压力值Pcr,见表6。 图9给出了七组典型(tR,LR,θ)数值下,耐压壳体的随厚度半径比fR的变化规律。其中是缺陷幅值为fR时的临界失稳压力是相同厚度下完善球壳的临界失稳压力。

表6 系列fR下耐压壳体的Pcr(MPa)Tab.6 Pcr(MPa)of pressure hulls for a series of fR
本文对F′(fR)的拟合考虑最危险的状态,如图9所示,选取所有离散点的外包罗线,其拟合表达式为:

(13)式的拟合结果即为图8所示的Ti-4-V-6钛合金三藕节切弧连接耐压壳体的缺陷项表达式。
4.3 f1′(tR)的确定
在确定Pcr与(tR,LR,sin(θ))之间的函数关系时,假定fR=0。
确定函数表达式f′(tR,LR,sin(θ))的方法类似于第3部分确定f(tR,LR,sin(θ))的方法,取以下五组典型(LR、θ)数值计算:(2.3,55°),(2.3,40°),(2.3,65°),(1.9,55°),(2.7,55°),系列tR下耐压壳体的临界失稳压力Pcr,见表7。图10给出了五组典型(LR、θ)数值下随厚度半径比tR的变化规律。其中是对应的耐压壳体的临界失稳压力是对应的耐压壳体临界失稳压力。
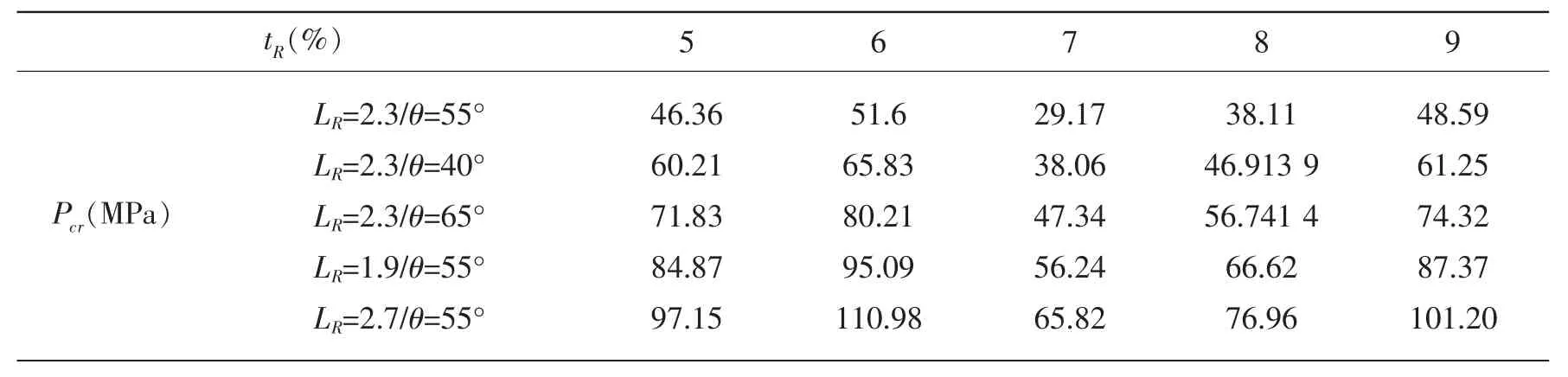
表7 系列厚度下耐压壳体的临界失稳压力值Tab.7 Pcrof pressure hulls for a series of thick

从图10可以看出,五组典型(LR、θ)数值下,耐压壳体的Pcr随tR的变化规律区域一致,对应点的误差不超过4%,可以近似认为tR是与LR、sin(θ)无关的独立参量,则(12)式可以写为如下形式:
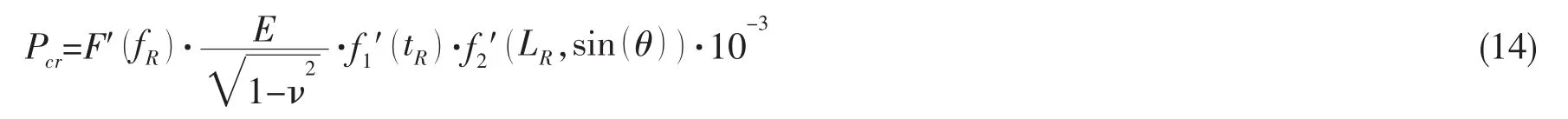

式中,a1′=-58.6,a2′=24.63,a3′=-0.437。
f1′(tR)的拟合误差不超过4%,其拟合曲线如图10所示。
4.4 f2′(LR,sin(θ))的确定
假定初始缺陷因子fR和耐压壳体的厚度半径比tR为定值:fR=0,tR=7%。
将F′(0)=1和f1′(7%)=1的取值代入(3)式得到:

其中Pcr的单位为MPa。
系列球壳间距半径比LR、连接角θ下耐压壳体的临界失稳压力列于表8,联合表8和(16)式求得函数f2′(LR,sin(θ)),并分别间隔选取几组典型离散点(LR,f2′(LR,sin(θ)))、(sin(θ),f2′(LR,sin(θ))),将其变化规律显示于图11、图12。通过反复尝试和误差比较,图11中的各组离散点采用二次多项式进行函数拟合可以获得较高的精度,图12需要用三次多项式拟合以满足精度要求。假定f2′(LR,sin(θ))的函数表达式如下:


表8 系列LR、θ下耐压壳体的Pcr(MPa)Tab.8 Pcr(MPa)of pressure hulls for a series of LRand θ


将{sini(θ)·Lj}(i=0,1,2,3;j=0,1,2)视为基函数,采用最小二乘法在商业软件Matlab中编写程序R求解{bk′}(k=1,2,…,12),{bk′}中各元素数值列于表9。

表9 {bk′}中各元素数值Tab.9 The value of{bk′}
(17)式的拟合误差列于表10,从误差表中可以看出,大部分数值拟合误差都在1%左右,最大误差为-3.83%~2.84%,用(17)式来拟合f2′(LR,sin(θ))可以满足精度要求。
因此(14)式即为线性材料的三藕节切弧连接耐压壳体强度公式,其中的f1(tR)、f2′(LR,sin(θ))分别由(15)式和(17)式求得。

表10 f2′(LR,sin(θ))的误差Tab.10 The error of f2′(LR,sin(θ))
5 结 语
本文采用有限元法,研究了最近提出的新型大深度潜水器耐压壳体—三藕节切弧连接耐压壳体的强度和稳定性性能;考虑初始缺陷和非线性的影响,采用最小二乘法进行数据拟合,提出了三藕节切弧连接耐压壳体的强度公式和稳定性公式。本文提出的理论公式具有一定的精度,可为大深度潜水器耐压壳体设计提供理论依据,并可进一步用于该新型耐压壳体的优化设计。
[1]远藤伦正.Research on pressure hull for deep submergence research vehicle made of titanium alloy[J].三菱重工技报,1986,23(4):58-62.
[2]陆 蓓,刘 涛,崔维成.深海载人潜水器耐压球壳极限强度研究[J].船舶力学,2004,8(1):51-58.
[3]李良碧,王仁华,俞铭华等.深海载人潜水器耐压球壳的非线性有限元分析[J].中国造船,2005,46(4):11-17.
[4]王仁华,俞铭华,李良碧.初始缺陷对深海载人潜水器耐压球壳弹塑性稳定性影响[J].海洋工程,2006,23(4):111-115.
[5]Liang Cho-Chung,Teng Tso-Liang,Lai Wen-Hao.A study of diving depth on deep-diving submersible vehicle[J].Pressure Vessels and Piping,1998,75:447-457.
[6]刘 涛.大深度潜水器耐压壳体弹塑性稳定性简易算法[J].中国造船,2001,42(3):9-14.
[7]Liang Cho-Chung,Shiah Sheau-Wen,Jen Chan-Yung,Chen Hung-Wen.Optimum design of multiple intersecting spheres deep-submerged pressure hull[J].Ocean Engineering,2004,31:177-199.
[8]伍 莉,刘土光,张 涛.藕节形大深度潜水器耐压壳体强度与稳定性分析[J].船海工程,2004,10:189-194.
[9]伍 莉,孟凡明,陈小宁等.藕节形大深度潜水器耐压壳体优化设计[J].船舶力学,2008,12(1):100-109.
