轴力作用下X型焊接管节点热点应力的分布规律
2010-09-22邵永波
邵永波
(烟台大学土木工程学院,山东 烟台 264005)
1 引 言
X型管节点在海洋平台结构中是一种常见的结构。由于这种结构是通过焊接而形成的,在沿着焊缝周围的区域存在着残余应力,通常这个区域称为热点应力区。热点应力区内的应力大小和分布情况决定着管节点的疲劳寿命大小。由于沿着焊缝交线周围刚度大小不均匀,在焊缝周围存在着应力集中现象,这种应力集中将导致X节点的疲劳寿命大大缩短。在热点应力区域内,沿着焊缝周围应力分布情况对管节点疲劳寿命也存在着影响。当焊缝周围最大应力点位于不同位置时,疲劳裂纹的扩展方式和过程是不同的。
对热点应力通常是采用一个力学参数—应力集中系数来评估的。为了便于应用,通常把应力集中系数表示成几何特征参数的函数。了解管节点几何特征参数对应力集中系数的影响对于评价管节点的疲劳寿命具有重要的意义。国内现有的对管节点应力集中系数的评价大都集中在T、Y和K型管节点上[1-4],有关计算数据和试验资料也比较完善。对于X管节点的分析,则报道得比较少,且研究也并不深入。此外,对于X管节点热点应力集中系数的研究,主要是以热点应力的大小为研究对象[5-7],对于几何特征参数对于热点应力位置的研究,则未见有关报道。
本文首先提出了一种X型焊接管节点的模拟方法,采用提出的模型,分析了轴力作用下X管节点焊缝周围的应力分布规律。然后通过对112个X节点模型进行的有限元分析,研究了X节点几何特征参数对焊缝周围应力大小和分布规律的影响,所得到的结果可为X管节点疲劳寿命做参考。
2 X焊接管节点的有限元模型
用有限单元法分析管节点结构时,计算结果的精度主要取决于两个因素:一是采取何种类型的单元来模拟整个结构;二是在网格划分的过程中,既要保证网格的疏密程度合适,又要保证单元不会过度被扭曲。在对管节点的模拟研究中,以前的方法大都采用壳单元来模拟整个结构。壳单元忽略了管壁厚度方向的剪应力的变化,而且壳单元很难灵活而精确地模拟焊缝的形状。Lee和Bowness[8]发现管壁内外表面的应力大小并不相同,这种差异是由于管壁厚度方向上的弯曲应力造成的。Herion等[9]提出:在计算管节点的应力集中系数时,三维二次六面体单元是最适合模拟带焊缝节点的单元。因此,本文将采用这种单元来模拟带焊缝的X节点。
焊接的X型管节点在焊缝周围存在着应力集中现象,所以这个区域的有限元网格应该划分得精密一些,以准确地反映应力梯度的变化。在远离焊缝处,由于应力梯度很小,破坏不会在这些地方发生,因此这些区域的有限元网格可以划分得稀疏一些,以减少计算所用的时间。同时,在应力梯度比较大的区域,即焊缝周围,网格中单元的质量要求比较高,这些单元应减少过度扭曲,以影响有限元计算结果的精度。要达到上述要求,可以采用一种分区域有限元网格划分方法。在这种网格产生方法中,根据计算精度的需要,将整个X节点划分为三种不同区域:精密网格区、过渡网格区和稀疏网格区。在主管(即弦管)和支管交线的焊接处,由于应力梯度大,这部分区域为精密网格区。在主管和支管上远离焊缝周围的区域,为稀疏网格区域。精密网格区和稀疏网格区通过过渡网格区连接在一起。
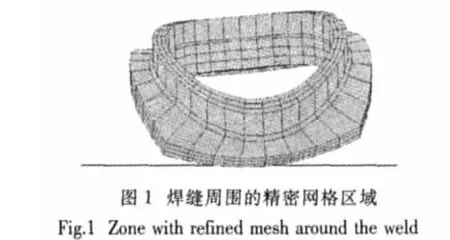
采用这种分区域网格划分法时,焊缝周围的网格划分如图1所示。在精密网格区域内,在主管和支管的管壁厚度方向上,划分了三层单元。沿着主管和支管交线的焊缝采用一层六面体单元模拟。由于六面体单元的尺寸可以灵活的变化,从而很容易准确地模拟交线周围焊缝尺寸的变化情况。
图2所示的为主管上远离焊缝的稀疏网格区域。在稀疏网格区域中,沿着管壁厚度方向上只划分了一层单元,并且单元尺寸逐渐变大,网格趋向稀疏。
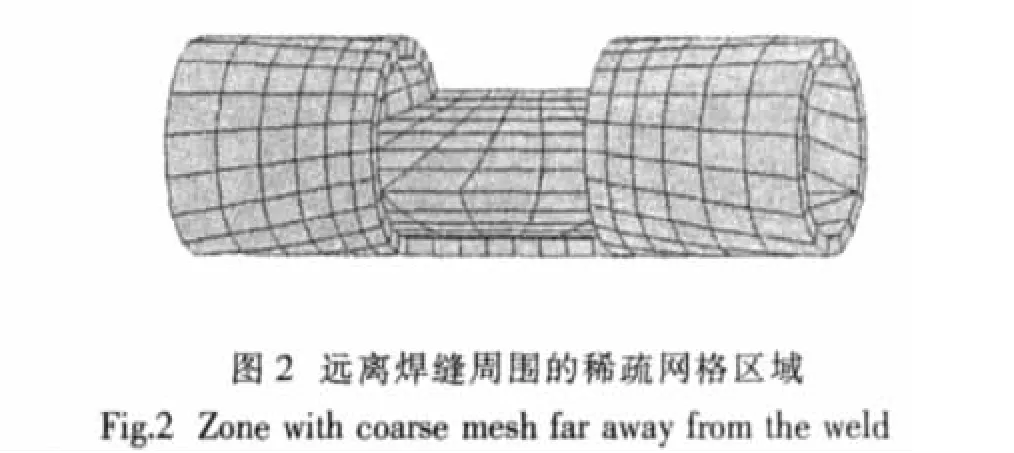
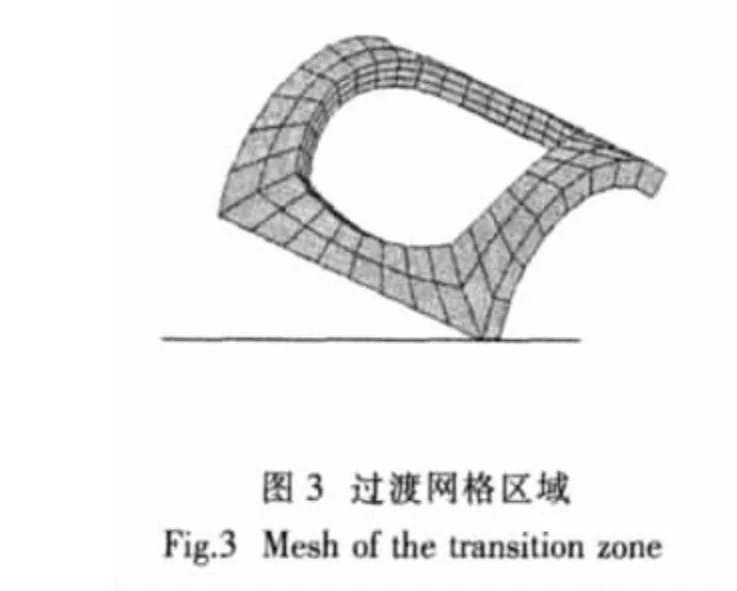
由于精密网格区域中,沿着管壁厚度方向上有三层单元,在稀疏网格区域内,沿着壁厚方向只有一层单元,所以需要一个过渡单元区来连接精密网格区域和稀疏网格区域。实现这个功能的为过渡网格区。图3表示出了连接图1和图2中网格区域的过渡网格区。图3的内边界是连接精密网格区域的,所以在厚度方向上有三层单元,而外边界是连接稀疏网格区的,所以在厚度方向上只有一层单元。通过过渡区域把精密网格区域和稀疏网格区域很方便地联系在一起,最后形成X节点的总体网格。
利用分区网格产生法,可以有效地控制不同区域的网格密度和单元质量,从而提高有限元结果的精度。当三种区域中的网格都独立产生后,可以将所有区域的网格合并在一起得到X节点的整体网格图,如图4所示。从图4中可以明显看出,在X节点不同区域,网格密度是不同的,这种有效地控制网格密度是分区网格法的优点所在。

3 X型管节点热点应力集中系数的计算
管节点热点应力集中系数是沿着焊缝周围最大应力与管节点名义应力的比值。承受轴力的X型管节点的名义应力可由下式计算:

其中Fa表示轴向拉力,d和t分别为支管的直径和管壁厚度,σn为名义应力。
如果轴力作用下X节点的热点应力为σh,则热点应力集中系数SCF为:

在(2)式中,需要定义热点应力。对于热点应力的定义还存在着不少争议,如国外有些文献中[8]定义热点应力为焊趾处最大的几何应力,即最大主应力。热点应力的另外一种定义[9-10]是沿着焊缝周围垂直于焊趾的应力,这种热点应力要小于最大主应力。后者对于热点应力的定义在评价管节点的疲劳寿命时更具有实际意义,因为节点的疲劳破坏表现为表面裂纹的萌生和扩展,表面裂纹的扩展路径是沿着焊缝周围,所以垂直于表面裂纹方向(即垂直于焊趾)的应力是表面裂纹的“张开”驱动力,这种定义下的热点应力对疲劳破坏起主要作用。在对X节点焊缝周围的应力分布进行分析时,也采用这种垂直于焊趾方向的应力为热点应力。
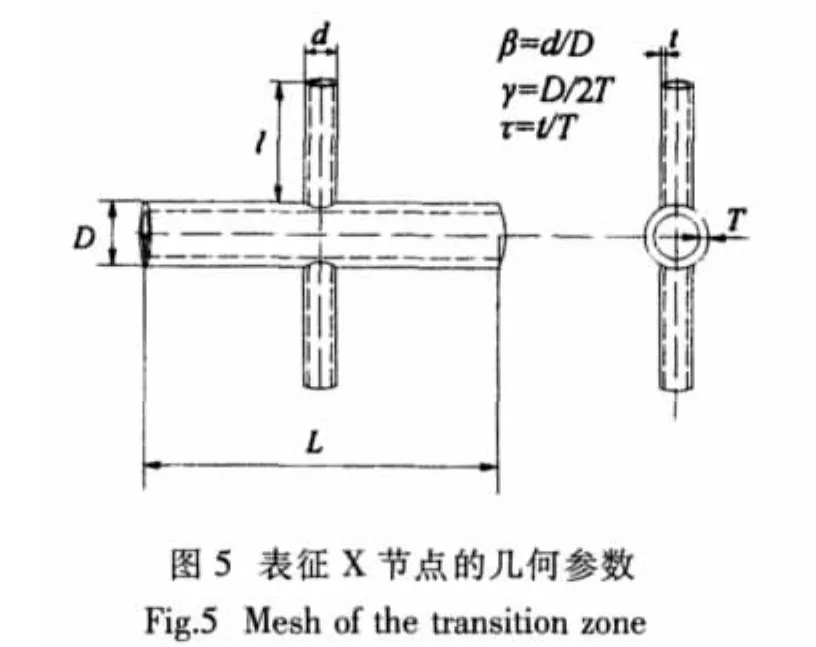
如前所述,管节点中系数力集中系数通常表示为节点几何特征参数的函数。对于轴力作用下的X型管节点,其应力集中系数主要由三个几何参数决定:表征主管厚度的参数γ(γ=R/T,R和T分别为主管的半径和厚度)、表征支管大小的参数β(β=r/R,r为支管半径)以及表征支管厚度的参数τ(τ=t/T,t为支管厚度),如图5所示。对于具有不同尺寸大小的X节点,如果它们的三个几何参数(β、γ和τ)大小相同,则认为它们具有相同大小的应力集中系数,这个结论已经得到有关研究者的证明[11]。
目前国内外对X管节点应力集中系数的研究比较少,尤其是有关试验测试的数据很少见到有关报道。文献[7]中对国外有关管节点应力集中系数的研究进行了总结,提到了一些关于X节点的试验结果,这些结果将用来作为标准来判断本文提出的有限元模型的准确性。文献[7]中所提供的两个轴力作用下X节点的几何参数以及应力集中系数的试验测试结果如表1所示。
从表1中可以看出,试验测试中的两个X节点试件的几何参数基本相同,所测试得到的两个节点试件的应力集中系数大小也基本相同。采用本文提出的有限元模型,对表1中的两个X节点进行了有限元计算,得到了沿着焊缝周围的应力集中系数的分布情况,如图6所示。在图6中,φ表示沿着焊缝周围的角度,其中0°位于冠点处,90°表示鞍点处。C1和C2分别表示X节点模型1和2的主管上应力集中系数分布,而B1和B2则分别表示X节点模型1和2的支管上应力集中系数分布。

表1 X节点几何参数及应力集中系数Tab.1 Geometrical parameters and stress concentration factor of X-joint
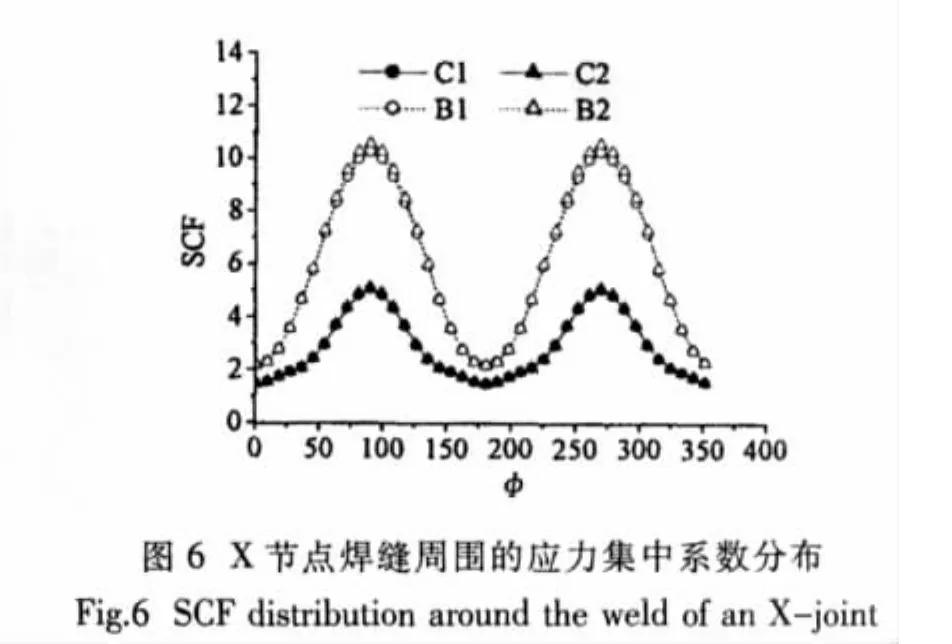
从图6中可以得到以下两个结论:(1)支管上的应力集中系数要比主管上的应力集中系数数值大;(2)无论主管还是支管上,鞍点处应力值最大,而冠点处应力值最小。从有限元结果中得到两个X节点的应力集中系数值分别为10.3和10.6。有限元结果与试验测试结果相比,其相对误差分别为5.5%和3.1%。显然,有限元结果可以提供很高精度的预测值,这也说明本文提出的有限元模型在分析X节点热点应力集中系数分布时是准确可靠的。
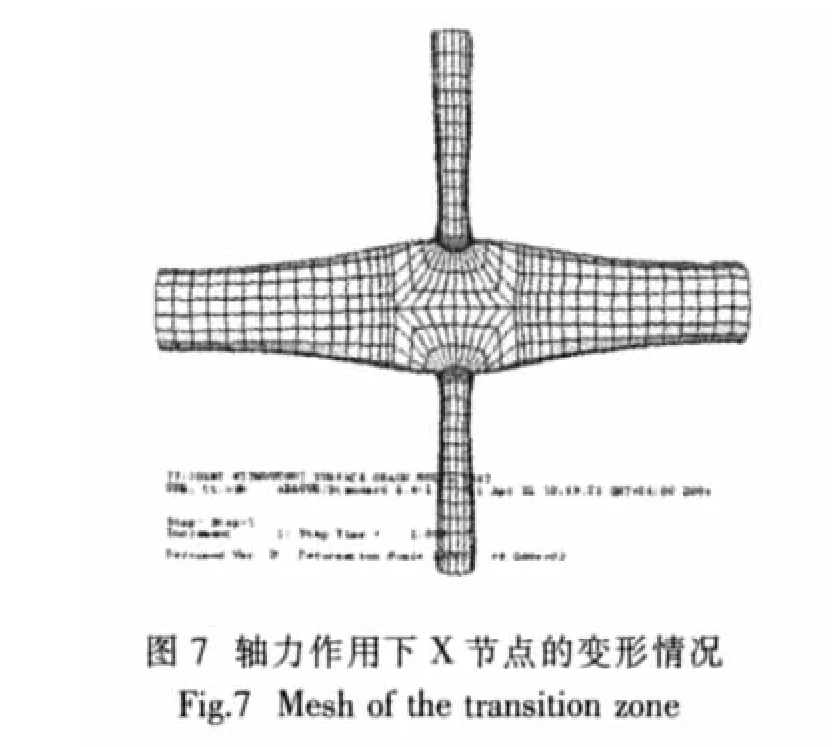
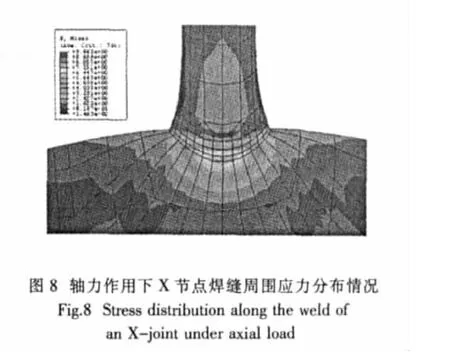
在轴力作用下X节点的变形以及焊缝周围应力分布情况分别如图7和图8所示。从图8的应力云图中也可以明显看出,在鞍点处的应力值达到峰值,而在冠点处的应力则很小。所以轴力作用下此X节点试件发生疲劳破坏时,疲劳裂纹将从支管的鞍点处萌生并沿着焊缝向两侧对称扩展。
4 X节点热点应力的大小和分布规律
由于X节点的应力集中系数是由几何特征参数决定的,为了研究几何参数对X节点应力集中系数大小和位置的影响情况,本文分析了112个不同几何形状的X管节点在承受轴力作用下沿着焊缝周围的应力集中系数分布规律。这112个X节点模型是根据几何参数β、γ和τ而进行划分的,其范围如表2所示。
在研究几何参数对X节点应力分布的影响时,主要考虑两个方面:一是对应力集中系数大小的影响;二是对焊缝周围应力集中系数分布的影响。
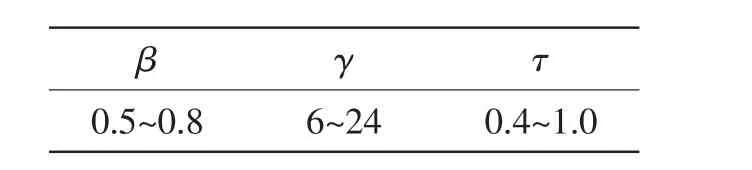
表2 X节点模型的几何参数范围Tab.2 Range of geometrical parameters of X-joint
4.1 参数β对应力分布的影响
参数β对X节点热点应力集中系数的影响如图9a和9b所示。β对主管和支管上应力集中系数的影响取决于另外两个参数γ和τ。在γ和τ比较大的时候,β对应力集中系数的影响并不是单调的,应力集中系数先是随着β的增大而增大,到一定程度后又随着β的增大而减小。在γ和τ比较小的时候,随着β的增大,应力集中系数逐渐减小。

参数β虽然对X节点应力集中系数的大小有影响,但是对热点应力的位置是没有影响的,这可以从图10a和10b中看出来。虽然参数β的变化会改变应力集中系数曲线上每个点的SCF值,但是无论是主管还是支管上,最大应力集中系数点,即热点应力位置,始终位于鞍点处。所以参数β的变化不会引起疲劳裂纹萌生位置的变化。
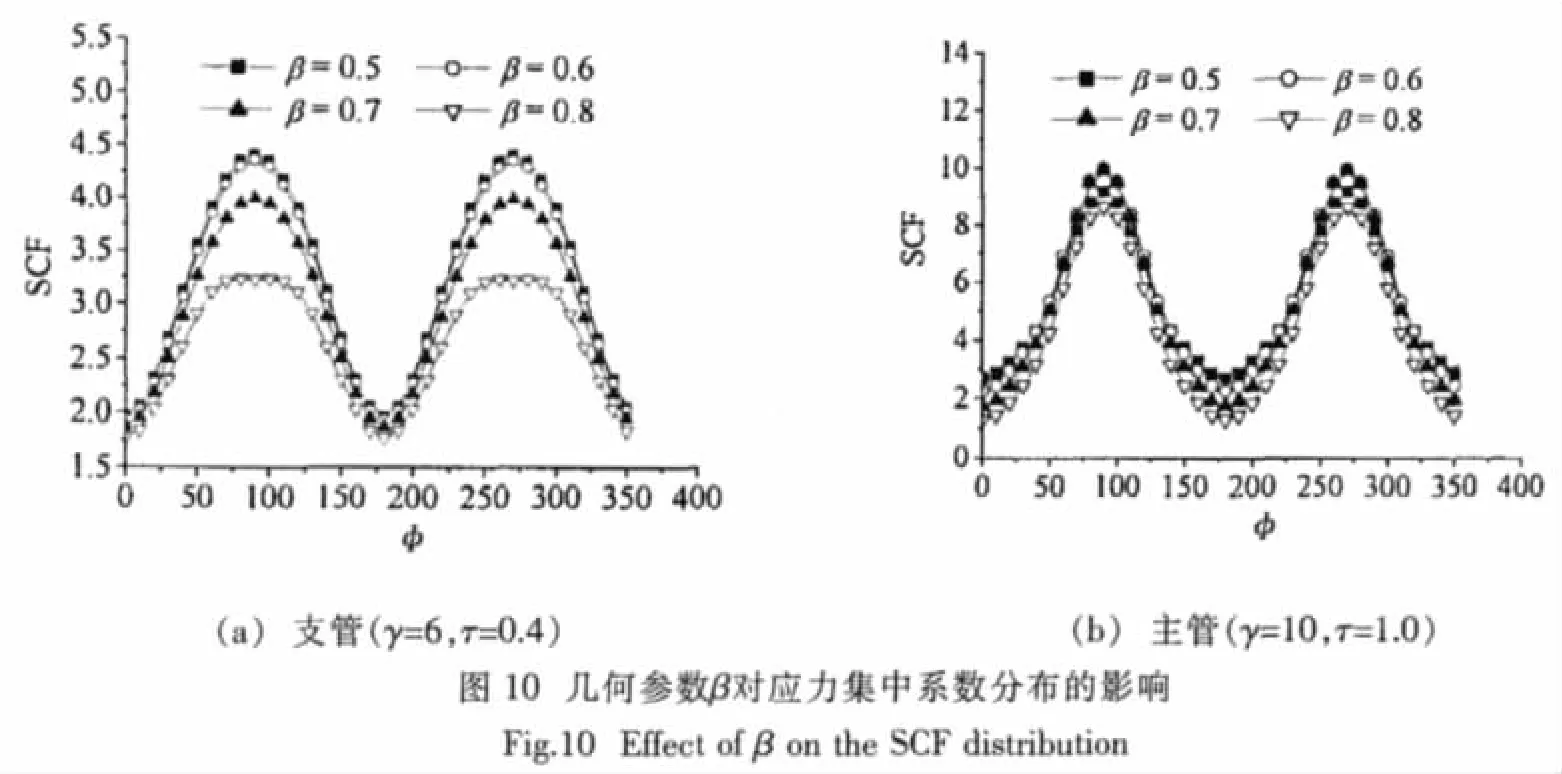
4.2 参数γ对应力分布的影响
参数γ对主管和支管上应力集中系数大小的影响是单调而有规律的。如图11a和11b所示,无论对于主管还是支管,随着参数γ的增加,应力集中系数SCF的值也随着增加,而且应力集中系数和参数γ之间的关系非常接近于线性变化。从应力集中系数随着参数γ的变化情况还可以发现:γ的变化引起应力集中系数的变化是非常显著的,这说明主管厚度大小对于应力集中系数的变化是很敏感的,它的变化对X节点疲劳寿命的影响是非常大的。
图12a和12b中显示了参数γ对于X节点焊缝周围应力分布规律的影响。参数γ的大小只对热点应力集中系数的大小有影响,但对于热点应力的位置则不起任何影响作用。在γ从6.0到24.0之间变化时,主管和支管上热点应力的位置始终位于鞍点处,而冠点处的应力集中系数值始终保持为最小。

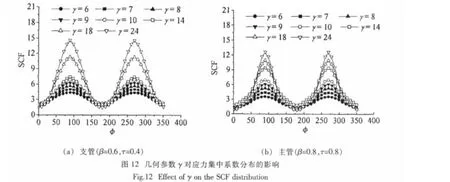
4.3 参数τ对应力分布的影响
参数τ对应力集中系数大小的影响是单调增加的,如图13a和13b所示。无论对于主管还是支管而言,参数τ的增加都将导致应力集中系数的增大。应力集中系数随着参数τ增加的幅度要受其它两个几何参数β和γ的影响。β和γ比较大的时候,应力集中系数随着参数τ增加而增加的幅度比较大;反之当β和γ比较小的时候,应力集中系数随着参数τ增加而增加的幅度比较小。

参数τ对X节点焊缝周围应力分布规律的影响如图14a和14b所示。与其它两个几何参数的影响规律相同,参数τ也只影响应力集中系数的大小而不改变热点应力的位置。无论参数τ取何值,热点应力始终位于鞍点部位,而冠点部位的应力也始终为最小值。
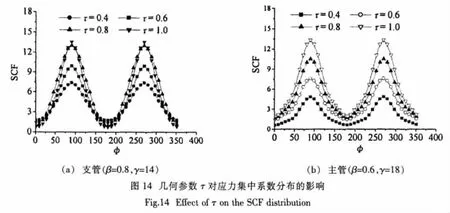
5 结 论
本文对焊接X型管节点提出了一种分区有限元网格产生方法。这种方法可以根据计算的需要在不同结构区域产生不同密度和质量的网格,从而可以有效地控制每个区域内网格中单元的大小和质量。利用提出的模型,采用有限元法分析了承受轴向拉力作用下的X节点在焊缝周围应力集中系数的大小和分布情况。
通过对112个X节点模型的有限元分析,调查了表征X节点的三个几何参数对焊缝周围热点应力大小和位置的影响情况,通过研究发现:
(1)主管厚度参数γ和支管厚度参数τ对主管和支管上的应力集中系数大小有着显著的影响,且影响规律是固定的,即随着这两个参数的增大,主管和支管上应力集中系数大小也随之增大;支管半径参数β对主管和支管上应力集中系数大小的影响规律不很明显,要受其它两个几何参数大小来决定,且β的变化对应力集中系数大小的影响并不十分显著。
(2)几何参数对轴力作用下X节点焊缝周围热点应力的位置无影响。无论三个几何参数大小如何,热点应力始终位于鞍点处,而冠点处的应力始终为最小值。这说明在轴向循环载荷作用下,疲劳裂纹将从鞍点处萌生,即破坏发生在鞍点处。
[1]陈铁云.近海钻井平台管状接头应力分析的进展[J].力学进展,1985,4(25):425-433.
[2]陈伯真.海洋平台管节点应力分析研究工作展望[J].力学进展,1987,17(3):331-336.
[3]李华明.海洋平台管节点的热点应力测量[J].振动、测试与诊断,1991,11(3):23-29.
[4]陈铁云,朱正宏.海洋平台T、Y、K及塔接K型管接头的弹塑性有限元分析[J].海洋工程,1992,10(2):8-15.
[5]Wordsworth A C,Smedley G P.Stress concentration at unstiffened tubular joints[C]//Proceedings of the European Offshore Steels Research Seminar.Cambridge,UK,Paper 26,1978.
[6]Smedley P,Fisher P.Stress concentration factors for simple tubular joints[C]//Proceedings of the 1st International Offshore and Polar Engineering Conference.International Society of Offshore and Polar Engineers,Edinburgh,UK,1991:475-483.
[7]王春光,李少甫,石永久.焊接钢管节点热点应力集中系数参数方程的适用性研究[J].工程力学,1999,16(6):44-53.
[8]Department of Energy.Offshore Installations:Guidance on Design and Construction[K].HMSO,UK,1984.
[9]van Wingerde A M,Wardenier J,Packer J A.Commentary on the draft specification for fatigue design of hollow section joints[C]//The 8th International Symposium on Tubular Structures.Singapore,1998:117-127.
[10]International Institute of Welding(IIW).Fatigue design procedure for welded hollow section joints[M].Abington Publishing,Cambridge,England,1999.
[11]Marshall P W.Design of welded tubular connections:Basis and use of AWS Code Provisions[M].Elsevier Science Publishers,Amsterdam,Netherlands,1992.
