农产品生产异常波动的预测与实证研究

罗光强，谭江林

（湖南农业大学 经济学院，长沙 410128）

农产品生产异常波动的预测与实证研究

罗光强，谭江林

（湖南农业大学 经济学院，长沙 410128）

经济市场化与供给多元化条件下农产品生产频繁波动是一个不可避免的特征事实。客观面对农产品生产的正常波动，努力防止和规避农产品生产的异常波动是一个值得研究的课题。文章首先给出了一个农产品生产异常波动的预测方法与模型，然后以湖南粮食生产为例进行了相关实证分析。

农产品生产；异常波动；预测方法

0 引言

2010年中央一号文件精神指出，要完善农产品市场调控机制，保持农产品市场稳定。这是针对当前国内外经济增长明显放缓和农产品生产波动的新形势，实施的一项保障农产品稳定增长的重大任务。因此，努力减少农产品生产波动，积极促进农产品生产稳定增长是一个值得研究的重大课题。既有的相关研究主要集中于各类农产品生产波动规律和趋势的分析，其目的是试图通过提供预期市场信号，发挥市场机制的调控功能，促进农产品生产的稳定增长。但是，由于农产品生产具有典型的弱质性特征，农产品生产存在的蛛网现象仅仅依靠市场功能是难以解决的，彻底消除或完全规避农产品生产的波动问题是不现实的。基于此，本文试图引进农产品生产异常波动的概念，并以湖南粮食生产为例展开农产品生产异常波动的预测研究，以便在客观面对农产品生产正常波动的规律条件下为防止和规避农产品生产异常波动的政府干预行为提供决策参考。

1 农产品生产异常波动的预测方法

1.1 研究方法

目前常用于预测趋势的模型大致包括以下几种：(1)回归关系类模型。这类模型的特点是被预测事物与其影响因素之间，在一定时间内保持着某种固定结构函数关系，可以通过一元或多元回归的方式来表述。(2)因果关系类模型，这类模型的特点是在被预测事物与其影响因素之间的关系是用因果形式描述的，Granger对此进行了深入研究，提出了Granger因果关系的计量经济模型。(3)投入产出测算法。该方法的主要观点是根据影响粮食生产的各种要素的投入状况来测算粮食的期望产量。(4)灰色模型。是以灰色生成函数概念为基础，以微分拟合为核心的建模方法，将杂乱无章的原始数据序列通过一定的处理方法弱化波动性，使之变为比较有规律的时间序列数据，再建立用微分方程描述的模型，该方法本质来讲也是一种时间序列模型。(5)时间序列模型。这种方法主要是通过建立预测对象与综合指数之间的时间序列相关辨识模型。该模型在预测方面的应用如今发展较快，博克斯—詹金斯方法是该领域发展比较成熟的模型，用回归移动平均模型(ARMA)、齐次非平稳模型(ARIMA)等来预测未来变化。本文将采用博克斯—詹金斯方法，以历年湖南粮食总产量为依据，通过其趋势图形拟合出与之相似的指数回归曲线，消除了原序列的长期趋势，根据对数据ADF检验后，发现其残差序列为一平稳过程，最终确定ARMA预测模型。利用ARMA模型和相关统计数据可以得到农产品生产的时间序列预测数据。然后通过预测数据的增长波动指数分析并定义异常波动指标即可判断出农产品生产异常波动的时间区域。

1.2 ARMA模型

首先，需建立自回归模型AR(p)，p阶自回归模型记作AR(p)，满足下面的方程：ut=c+φ1ut-1+φ2ut-2+…+φput-p+εt,其中：参数 c 为常数；φ1，φ2， …，φp是自回归模型系数；p 为自回归模型阶数；εt是均值为0，方差σ2为的白噪声序列。其次，建立移动平均模型MA(q)，q阶移动平均模型记作MA(q)，满足下面的方程：ut=v+εt+θ1εt-1+…θqεt-q,其中：参数 v 为常数；参数θ1,…,θq是 q 阶移动平均模型的系数；εt是均值为 0，方差 σ2为的白噪声序列，这样就可以得到ARMA(p,q)模型：ut=c+φ2ut-1+…+φput-p+εt+θ1εt-1+…θqεt-q。当然在估计 ARMA(p,q)具体的步骤估计之前要检验时间序列的平稳性，特别是要检验其是否含有单位根及所含有的单位根的个数。

2 农产品生产预测的实证分析

为了研究的方便，以下我们以湖南粮食（水稻）为例进行农产品生产预测的实证分析，其数据来源于湖南统计年鉴，文章中的计量分析软件采用Eviews5.0。

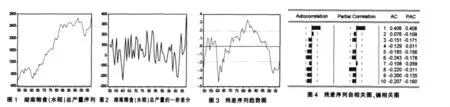
2.1 农产品产出预测模型的识别

我们首先对湖南粮食产出历年的统计数据进行时间序列分析和一阶差分分析，并将其结果描述成如图1和图2所示。由图1可以看出，湖南粮食总产出总体上呈上升的趋势，近似为一条波动向上的指数函数曲线。由图2显示其一阶差分序列，从图2可以看出湖南粮食总产出变化总体上呈现出频繁波动状态，在1997年到2008年（由于研究的起始时间为2009年，故其统计数据的选择年限为2008年）这段时间内，出现了上下振荡幅度较大，意味着湖南未来粮食产出波动有可能继续延续下去的趋势。

对于含指数趋势的时间序列来说，我们可以通过取对数来将指数趋势转化为线性趋势，即为lny，其拟合结果如下：

图3和图4为拟合结果的残差序列自动生成图形，由图3可以看出其残差序列基本上为一平稳序列。进一步从图4的偏相关分析,偏相关系数在滞后一期时明显不为0，在k＞2以后都处于95%置信区间内，说明序列的偏相关函数具有截尾性，所以P可以取1；从自相关分析可知，自相关系数在滞后一期时明显不为0，在k＞2以后都处于95%置信区间内，说明序列的自相关函数具有截尾性，所以q可以取1，因此对残差序列可以建立ARMA(1，1)模型。

2.2 农产品产出ARMA模型的建立

通过上述模型的识别,确定农产品产出ARMA(p,q)的预测模型如下：

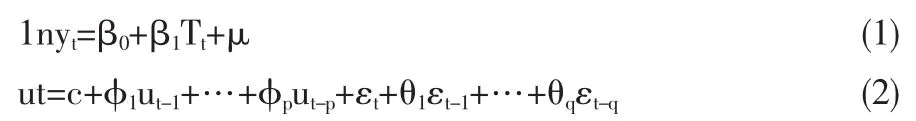
利用统计数据通过上述模型回归计算，得到估计方程为:

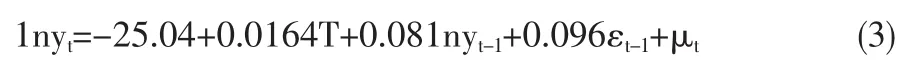
对方程进行估计后,应该对ARMA模型的适合性进行检验，即对模型的残差进行自噪声检验。如果残差序列不是白噪声序列，意味着残差序列还存在有用信息没被提取，需要进一步改进模型。通过对残差序列进行ADF检验，其残差序列如图5所示。

由图5可知，首先模型的残差序列是平稳的，说明模型通过了适应性检验，其次模型的拟合值与实际值保持大体一致，说明模型的预测结果可靠性也是很高的。说明指数回归ARMA(1,1)模型的短期预测能力是非常理想的。根据2008年湖南粮食总产出为2230万吨，这一结果与ARMA(1,1)模型的预测结果比较接近，这充分说明了ARMA(1,1)模型适用于粮食总产出中、长期预测。

2.3 农产品产出数量的预测

通过得到的回归模型（7），将对湖南未来10年间的粮食总产量进行中长期预测，得到的结果如表1所示。

3 农产品生产异常波动的预测

首先根据表1计算湖南粮食总产出趋势值的波动指数。所谓农产品生产波动指数指的是农产品实际产出增长率围绕其长期趋势上下波动的量值,它是衡量农产品生产周期波动幅度对历史增长趋势偏离程度的标准化指标,其波动指数的绝对值越大,说明农产品实际产出增长率偏离其长期趋势的程度越大,农产品的产出增长越不稳定,反之,其产出增长相对稳定。其计算公式为:V=/Y,其中,=,Y=,V为波动指数,y为实际经济增长率,Y为y的算术平均值,为标准差,n为实际值的样本数。湖南省2009～2018年粮食产出预测值的增长波动指数值如表2。

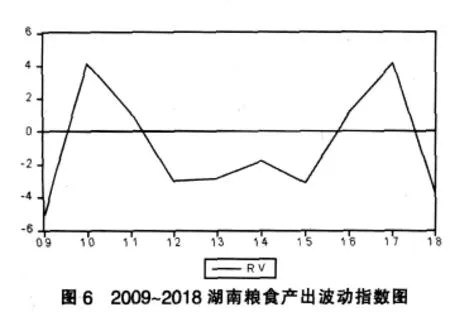
将表2描述成图形，即为农产品生产趋势增长波动轨迹，如图6所示。

表1 2009～2018年湖南粮食总产出预测值 （单位:万吨）

表2 2009～2018年湖南粮食总产出预测值的增长波动指数 （单位:万吨）

根据图6，我们发现从2009年至2018年以及其后的10年内，湖南粮食产出将总是处于不稳定状态，波动幅度大，并呈逐年增大趋势。如果将农产品生产波动指数超过3%定义为异常波动，则由表2和图6可知，如果不考虑已经过去的2009年，则预计湖南粮食产出在未来17年时间内的2010年、2012年、2015年、2017年和2018年等5年时间可能会出现异常波动状态。

4 研究结论

通过引进异常波动概念，运用预测模型可以对农产品生产波动趋势的异常状态发生的可能时间进行分析和判断，由此政府可以利用预测信息进行农产品生产异常波动的防范行为干预，例如，储备行为、期货行为和政策行为等。这样有利于促进农产品市场供求的动态均衡，有利于消除农产品生产中的“大起大落”现象，有利于降低农产品生产中蛛网现象引致的不利影响，有利于实现农产品生产的稳定增长。

[1]Mordecai Ezekiel.The Cobweb Theorem[J].The Quarterly Journal of Economics,1938,52(2).

[2]Itshak Borosh,Hovav Talpaz.Multi-Frequency Cobweb Model[J].American Journal of Agricultural Economics,1975,57(1).

[3]张淑娟，何勇.基于趋势一状态预测方法的粮食产量预测[J].浙江大学学报，2000,（4）.

[4]张素文，李晓青.湖南省粮食生产变化趋势及影响因子研究[J].国土与自然资源研，2005,(1).

[5]丁晨芳.组合模型分析方法在我国粮食产量预测中的应用[J].农业现代化研究，2007,（1）.

[6]高铁梅.计量经济分析方法与建模--Eviews应用及实例[M].北京：清华大学出版社,2006.

F201

A

1002－6487（2010）22－0082-02

国家社会科学基金项目（08BJy111）；湖南省社会科学基金项目（07DJ33）

罗光强（1963-），男，湖南湘乡人，教授，博士生导师，研究方向：产业经济。

（责任编辑/浩 天）