基于粗糙集理论的应用型本科院校英语教师科研水平评价研究
2010-12-12尹付,尹川
尹 付,尹 川
(1.常州工学院 外国语学院,江苏 常州 213002;2.四川理工学院 自动化与电子信息工程学院,四川 自贡 643000)
基于粗糙集理论的应用型本科院校英语教师科研水平评价研究
尹 付1,尹 川2
(1.常州工学院 外国语学院,江苏 常州 213002;2.四川理工学院 自动化与电子信息工程学院,四川 自贡 643000)
粗糙集理论是一种新型的处理模糊和不确定数据的数学工具,将粗糙集理论运用于应用型本科院校英语教师科研水平评价具有可操作性和准确性等特点. 利用粗糙集理论对江苏省某些应用型本科院校的 50名英语老师科研水平进行的随机调查数据表进行处理计算得出决策属性的影响度并分析其结果. 结果表明:研究结果可以为学校教学评估和教育评价以及学校教育管理提供理论支撑.
粗糙集理论;应用型本科院校;科研水平
随着信息技术的高速发展,人类产生并积累了大量的数据,然而这些数据中却存在着不确定性因素. 在这些大量的不确定数据背后隐藏着许多重要信息,充分利用这些重要信息可以很好地支持人们的决策. 当数据越来越多,数据规模急剧增长时,如何不被信息淹没,如何能够科学、合理、正确、有效地利用这些数据以产生对人们有用的信息和知识己成为当下一个非常令人关注的课题[1]. 迄今为止,一般只会利用简单而单一的概率统计方法来研究科研水平,而这种传统的方法有着很大的局限性,它只能从感性上说明问题,得到模糊、抽象的结论,并不能给人以直观的确定的结果. 随着社会的进步,这种模糊的分析方法已经不能满足人们的需求,而利用粗集理论来分析就可以弥补这样的不足[2].
本文利用粗集理论的条件属性约简方法,分别以应用性本科院校英语教师的科研申请项目数量、教材出版数量、发表论文数量、科研时间投入量、学历学位、图书拥有册数、教师职称、教师教龄、教师性别作为条件属性,以教师的科研水平作为决策属性,以江苏省不同的应用性本科院校共 50名英语教师作为研究对象,从而得出各个条件属性对结果的重要性差异,并应用粗集理论中知识的依赖性,分析出各个条件属性对目标的依赖性和重要程度,结果更为具体、量化.
1 粗集理论的概念阐释
粗糙集理论(Rough Set,又称粗集理论),是波兰数学家Z·Pawlak于1982年提出的新的数学理论. 这一方法与概率统计方法,模糊集方法和证据理论方法等其它处理不确定性问题理论的最显著区别是它无需提供问题所需处理的数据集合之外的任何先验信息. 同时,由于该理论未能包含处理不精确或不确定原始数据的机制,使得该方法与其它处理不确定性问题的理论有很强的互补性,因此对问题的处理比较客观[3].
为了更好地介绍粗集理论的应用,这里有必要先具体解释一下几个重要的基本概念.
信息系统及研究论域 信息系统的基本成分是研究对象的集合,关于这些对象的知识是通过指定对象的属性和它们的属性值来描述的. 一般来说,一个信息系统S可以表示为四元组. S= f(U ,R,V,F),其中U为论域,是对象的非空有限集合,既研究对象的集合;R是属性的非空有限集合,就是条件属性;V是属性值的集合,F: U×R→V是一个信息函数,它指定U中每一个对象x的属性值. 通常信息系统S= f(U ,R,V,F)也可简记为 S=(U, R).
离散归一化处理 在智能信息处理中,很多时候遇到对事物的描述可能是定性的说明,也可能是数据的表达,表达可能是有层次分别的,也可能是无序的某种性质. 而定性就是比较模糊的,比较不精确的,粗集理论的研究则需要一个定量的准确的数据库. 因此,就有了把定性的信息转变为定量数据表的问题,这就是离散归一化处理. 而离散归一化的方法应满足归一化后的空间维数尽量小和归一化后信息丢失尽量少这两个特点[4].
上近似,下近似,边界正域以及负域 在讨论的论域U中,存在子集X∈U,定义R为一等价关系. 当X能用R属性集确切的描述时,它可用某些R基本集合的并来表达,称X是R可定义的,否则X为R不可定义的. 假设给定知识库 K=(U, R),把U中所有一定能归入X的元素的集合称为X的R正域,既POSR(X). 用数学表达式表达就是 R_(X )={ X⊂ U:[X ]R⊂X }而当R−(X )={ X⊂ U:[X ]R∩X ≠}时,是上近似集. 此时上近似集中一定不能归入下近似集的部分就被称为X的R边界,既 BNR(X),U中一定不能归入X的集合就成为X的R负域,数学表达式为 NEGR(X).
属性简化 在实际工程应用中,系统表达中并不需要定义全部的知识,也就是说在用一系列属性来描述系统时,有一些属性是冗余的,去掉冗余的属性就可以达到简化系统的目的,而简化的这个过程就是属性简化[5].
给定知识库 K=(U, R),对于所研究的系统U,定义一个等价关系 R∈ind( K ),令R为一等价关系,则作下面的定义:
地理国情普查作为一项全面的地理空间大调查,工作作业范围广、涉及部门多、成果丰富,服务于国家发展的方方面面,经济建设的各行各业。在当前形势下,地理国情普查的成果转化与应用推广,对于测绘工作者来说既是挑战更是机遇。我们应当以地理国情普查为契机,突破传统测绘的局限性,逐渐丰富其内容覆盖的广度与深度,融合不同领域专业知识,面向政府部门、专业机构、社会公众的不同需求,创新地理信息产品,提供多样化的应用成果和技术服务,实现测绘与地理信息事业的转型升级。
如果 ind( R ) = ind( R − {r}),则r为R中可省略的,否则r为R中不可省略的. 在一些近似表达中,有一些特征没有作用,可以去掉这些特征而不影响对研究对象的表达.
核 对于任一r∈R,R不可省略,则族R是独立的;当K独立,且 ind( K) =ind( P),K⊆P为P的简化;P中所有不可省略关系的交集,称为P的核,记作core( P).
2 属性重要性的计算
上面介绍了属性简化的定义及方法,那么具体是如何来计算每个条件属性对决策属性的重要性,下面将给于比较详细的阐述.
首先令知识库 K=(U, R),且P, S∈U,那么存在的性质:(1)当 ind( P) =ind( S),知识S依赖与知识P;(2)当P→S且S→P,知识P和S是等价的,记为P≡S;(3)当不存在P→S,且不存在S→P,P,S为独立的[5].
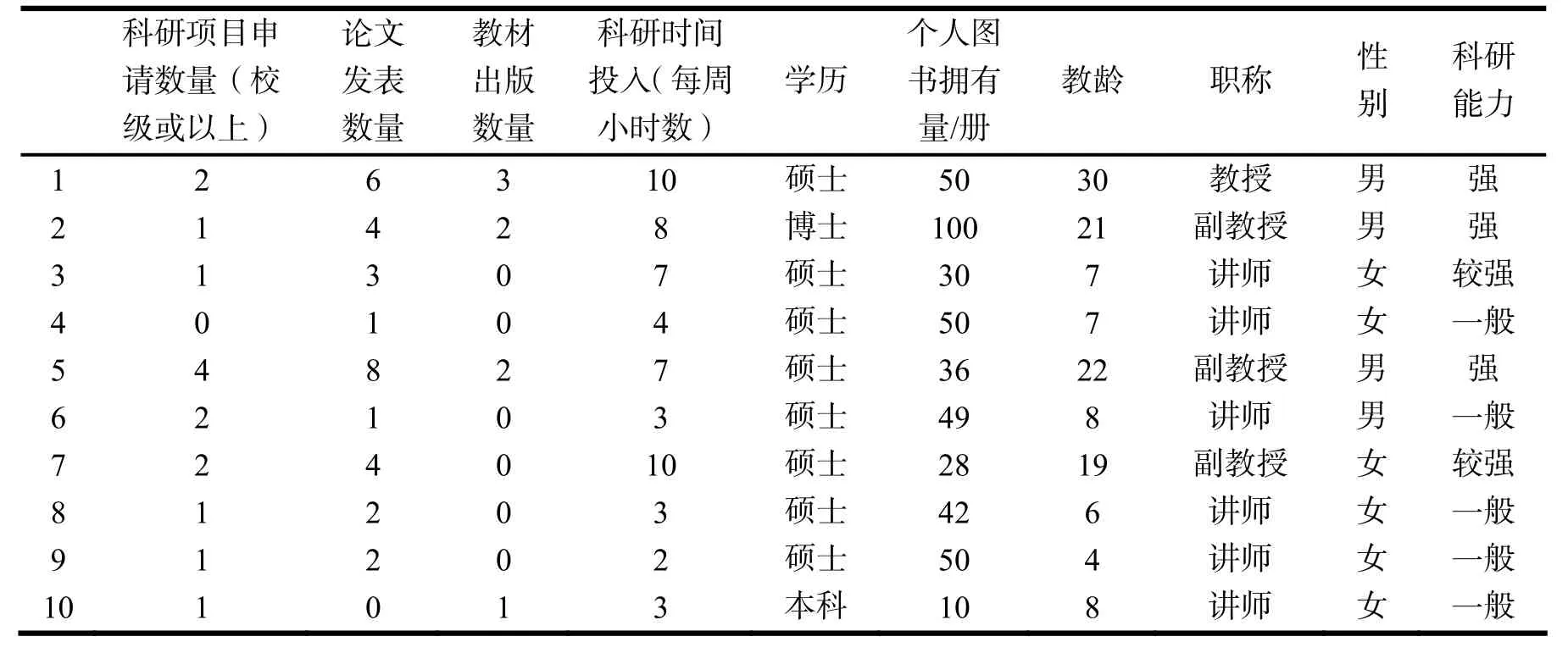
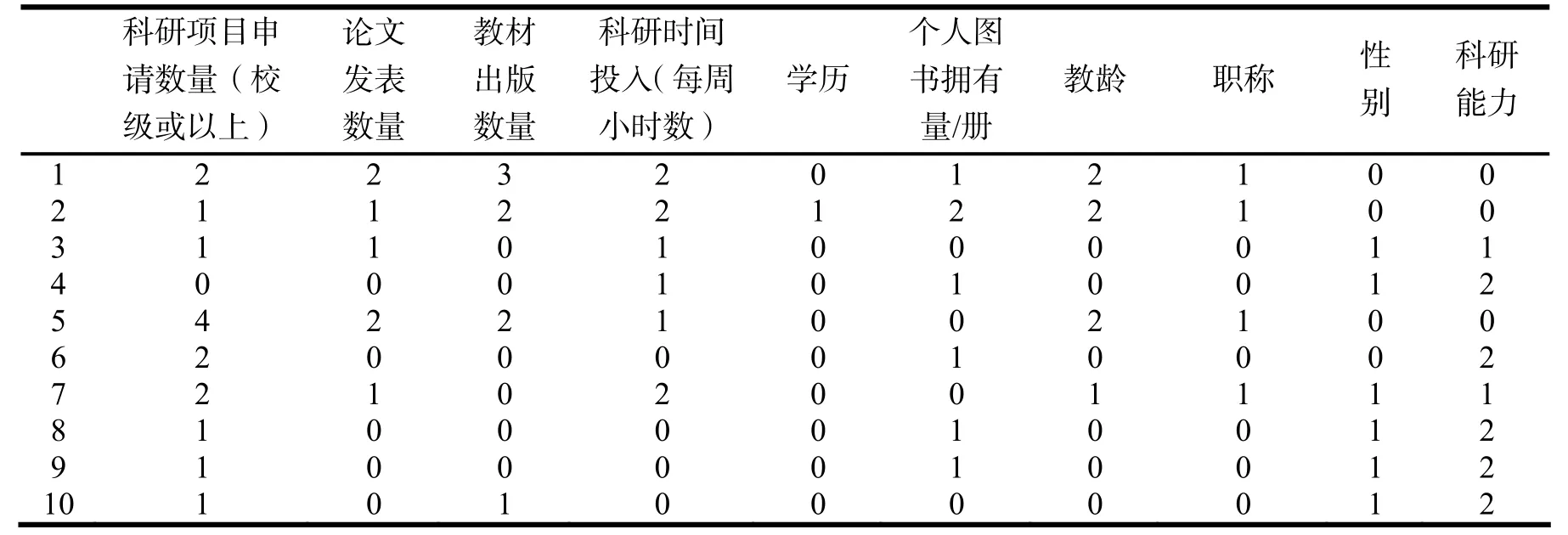
这里 card( P OSP(S ))为决策属性的个数 card( U )为条件属性的个数,当K=1时,称S是由P全可导的;当0 设(U, C ∪D, F)是一个决策表,其中C和D分别为条件属性集和决策属性集,属性子集C'∈C关于D的重要性定义为,(特别地,当C'=a时,属性a∈C关于D的重要性为: PCD(a) = rC(D ) − rC−a(D))[7]. 以上是从理论上分析条件属性对决策属性影响度的计算,下面就把它应用于目标知识系统,利用属性简约的方法对教师的各个属性进行分析. 这里是对江苏省某些应用型本科院校的50名英语老师进行的随机调查,得到的数据表如表1(只给出前10名教师的调查情况): 表1 对英语老师的随机调查表 首先对表1的原始信息进行离散归一化处理,在此之前要先对上述的条件属性进行定义,并将条件属性设置为P,则根据表1可以看出P{1}、P{2}、P{3}、P{4}、P{5}、P{6}、P{7}、P{8}、P{9}这样9个元素. 它们分别表示英语教师的科研申请项目数量、发表论文数量、教材出版数量、科研时间投入量、学历学位、图书拥有册数、教师教龄、教师职称和教师性别. 定义论文发表的数量2篇或2篇以下的为0,2篇到5篇的为1,而5篇以上的为2;科研时间投入量小于或等于3h以下为0,4h到7h为1,大于7h的为2;学历为硕士或硕士以下为0,硕士以上为1;个人图书拥有量40册以下为0,40册到80册为1,80册以上为2;教师教龄10年以下为0,10年到20年为1,20年以上为2;教师职称副教授以下为0,副教授或教授为1,定义男性为0,女性为1,教师的科研水平为决策属性,分别有强,较强,一般这样三个属性值,把它们分别定义为0、1、2这样三个数. 至此已经全部定义了上表中的所有属性,接着,把定性的属性值按照定义归一化成定量的属性值得到表2(只给出前10名教师的调查情况): 表2 归一化后的调查表 得到上面的归一化后的知识系统后,就可以进行计算分析,首先可以对上表进行属性的简约,通过检验 ind( R ) = ind( R − {r})这样的条件来确定线性无关的属性. 经过分析可以发现 ind( U ) = ind( U − P{9}),即教师的性别对他的科研能力是没有影响的. 接着对剩下的8项条件属性分别根据计算公式计算他们的重要度. Card( U)= 100,条件属性P{1,2,3,4,5,6,7,8},决策属性S{教师的科研能力}. 然后计算各个条件属性的重要性: 其余的各项也是通过上述方法来进行计算,他们分别是教材出版数量0.18,科研时间投入量0.12,教师学历0.08,个人图书拥有量0.07,教师教龄0.04,教师职称0.05. 从上面的计算结果来看,可以较为清楚地了解对应用型本科院校英语教师的科研水平进行分析的结果.此项研究结果可以为学校教学评估和教育评价以及学校教育管理提供理论支撑. 当然,不能认为这种评价就是完美无缺,它还需要教育管理部门和评估机构的尝试和验证,希冀能为应用型本科院校的英语教学目标实现和人才培养以及教师个人的科研水平提升都起到积极的作用. [1] PAWLAK Z ROUGH. Set theory and its applications to data analysis[M]. The Netherlands: Kluwer Academic Publishers,1991. [2] 曾黄麟. 粗集理论及其应用——关于数据推理的新方法[M]. 重庆: 重庆大学出版社, 1996. [3] 姚 毅. 知识发现中概率统计与粗集方法的比较[J]. 四川轻化工学院学报, 2003(2): 9-15 [4] 曾黄麟, 姚 毅. Image Recognition Using Adaptive Fuzzy Neural Network And Wavelet Transform,Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing[J]. Springer-Verlag, 2003: 635-639. [5] 尹 川, 姚 毅. 基于粗集理论的教师教学水平分析[J]. 河北软件职业技术学院学报, 2009(3):34-36. [6] 张文修, 吴伟志, 梁吉业, 等. 粗集理论与方法[M]. 北京: 科学出版社, 2001. [7] 刘 清. Rough集及Rough推理[M]. 北京: 科学出版社, 2003. [8] 石纯一. 数理逻辑与集合论[M]. 北京: 清华大学出版社, 2000. Assessment on the English Teachers’ Researching Proficiency in the Application-Oriented Colleges Based on the Theory of Rough Set YIN Fu1, YIN Chuan2 The theory of Rough set is a new mathematical tool which deals with the fuzzy and uncertain data. It has the characteristics of operability and accuracy to apply the theory of Rough set on the assessment of the English teachers’ researching proficiency in the application-oriented colleges. By means of the theory of Rough set, the investigated data at random in the table on the fifty English teachers’ researching proficiency from the application-oriented colleges in Jiang Su province has been calculated and dealt with, by which the affecting degree of decision attributes has been got and the result has been analyzed. It proves that the result of the research can provide the theoretical support for teaching assessment, education evaluation and college management. Rough set theory; Application-oriented colleges; Scientific research proficiency H0-05 A 1009-2854(2010)08-0005-04 2010-06-15 尹付(1963- ), 男, 安徽和县人,常州工学院外国语学院副教授, 上海外国语大学在读博士, 研究方向为: 英语教学法, 认知语言学. 饶 超)3 实例应用
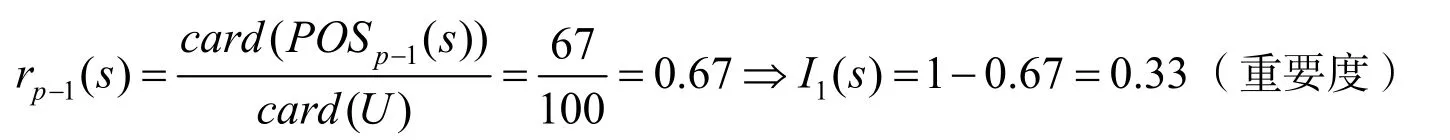
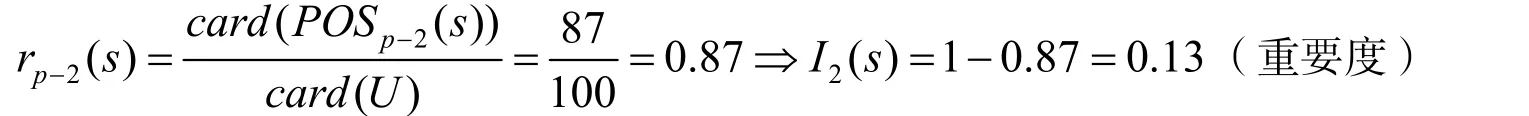
4 结语
(1.School of Foreign Language, Changzhou Institute of Technology, Changzhou 213002, China;2.School of Automation and Electronic Information Engineering, Si Chuan University of Science and Technology, Zigong 643000, China)
