蛋白质与线性DNA片断结合过程中的末端效应

2010-12-12杨晓静刘曦励娄春波欧阳颀

物理化学学报 2010年7期

杨晓静刘曦励娄春波欧阳颀

(北京大学理论生物学中心,物理学院,北京 100871)

How a protein molecule searches for short pieces of targets amid a flood of non-target sequences in the genome is a central question in molecular biology[1-5].Many in vitro techniques have been employed to investigate the DNA-protein interaction:filter binding is based on the protein′s ability to bind to nitrocellulose[6-7],while the electrophoretic mobility shift assay(EMSA)is operated on the principle that DNA-protein complexes migrate more slowly than an unbound DNA probe[8].One of the biggest differences between in vitro and in vivo experiments is that DNA fragments used for in vitro experiments are usually much shorter than genomic DNA.As a result,a significantly higher concentration of DNA ends exists in vitro than in vivo.Therefore,it is necessary to consider the potential effects caused by linear DNA ends before comparing in vitro and in vivo data.

The first potential end effect in linear DNA is the possibility that a protein has a higher probability of dissociating from end sites than from internal sites.Several investigators have addressed this issue in different systems,and the various studies have surprisingly produced contradictory results.In 1996,Surby et al.[9]showed that EcoRI methyltransferase have a higher dissociation rate from DNA ends during facilitated diffusion by simultaneously monitoring dissociation from a circularized DNA and its identical linearized form.Two years later,the opposite result was reported from a study comparing EcoRV(one kind of restriction endonucleases,an enzyme that cuts double-stranded or single-stranded DNA at specific recognition nucleotide sequences[10])cleavage rates of a biotinylated DNA fragment with approximately 500 bp(base pair)long in the absence and presence of avidin[11].In this report,a similar cleavage rate led to the conclusion that proteins do not exhibit an increased dissociation rate at DNA ends.However,both studies failed to control for multiple factors other than end effects,such as super-helix formation by closed-circular DNA in the Surby experiments[9]and the potential effect of negatively charged biotin on the chargecharge interaction between DNA and the protein in the EcoRV experiment.These multiple variables complicate interpretation of the results,so the issue of end effects remains uncertain.

Motivated by the open questions,we conducted a series of realtime experiments examining the binding of transcription factors (TFs)to DNA.To simplify the issue of the end effect,we employed nonspecific DNA fragments of different lengths,where each fragment could be considered to have comparable number of potential binding sites.In order to monitor both the association and dissociation processes in real time,especially for cases of nonspecific binding,we used surface plasmon resonance (SPR).In order to maintain the ends of the DNA fragments in a free state,we immobilized the protein on the chip surface.In order to investigate effects of the location of the binding sites on the fragment,we measured the binding affinities between protein and DNA fragments that contained a defined binding site at various positions.In order to be able to evaluate the effects of DNA sequence and to avoid nonspecific binding to secondary sites,we employed the Mnt repressor,which has an established specific binding energy matrix that can be used to evaluate sequence specificity[12-14].

The Mnt repressor is a DNA-binding protein that acts as a transcription inhibitor in the Salmonella phage P22.It has a ribbonhelix-helix structure and exists as a tetramer in solution,with each dimer binding to one half of a nearly symmetric 21 bp operator:ATAGGTCCACGGTGGACCTGT.Only the 17 bp underlined sequence in the center contributes significantly to binding[12-13,15].For all of our experiments,the reported concentrations of Mnt repressor refer to concentrations of the tetramer.

1 Materials and methods

1.1 Protein expression and purification

The gene encoding wild-type Mnt repressor was generated by PCR from the genome of Salmonella phage P22 and subsequently cloned into the NdeI/XhoI site of pET-21a(+)(Novagen), which contains a T7-promoter and His6tag at the C-terminus. The protein was expressed in Escherichia coli strain BL21 and purified under denaturing conditions by chromatography on ProBond resin(Invitrogen),with 100 mmol·L-1imidazole in the elution buffer.The purified protein was dialyzed against 2 L buffer containing 50 mmol·L-1Tris-Cl,pH 7.5,100 mmol·L-1KCl,0.1 mmol·L-1EDTA,and 50 g·L-1glycerol,and stored at -80℃.Purity of the protein was found to be at least 95%by SDS-PAGE and Coomassie blue staining.Protein concentration was determined using the Bradford method[16],with spectrophotometric analysis at 595 nm.

1.2 Oligonucleotide design and synthesis

A 71-nt(units of nucleotides)DNA fragment containing a natural Mnt repressor binding site was synthesized by Sango(China) or Takara(Japan).Following the manufacturer′s instructions, plasmid pQO2 was constructed by inserting the 71 bp DNA fragment into the pMD 18-T vector(Takara Bio,Japan),whereas pQO1 was constructed directly by ligating the two ends of the pMD 18-T vector.Different linear DNA fragments for SPR experiments were generated by PCR using different primers under the following conditions:94℃for 5 min,1 cycle;94℃for 30 s,60℃for 30 s,72℃for 30 s,25 cycles;72℃for 7 min,1 cycle.Table 1 lists the primers used for each fragment.Products were electrophoresed on 10-20 g·L-1agarose gels,and the bands of appropriate size were removed and purified with the QIAquick gel extraction kit(QIAGEN).The DNA concentrations were measured by calculating the difference between absorption at 260 nm and 320 nm(A260-A320).A schematic view of the experimental design is shown in Fig.1.

To ensure that the Mnt repressor could bind to the DNA fragments only at the natural Mnt repressor binding site,all fragments used in the interaction experiments were scanned using a specific binding energy matrix[14].We obtained a mean relative energy value of~21kBT,except for one potential binding site, which received a maximum score of~6.8kBT.The binding energy difference between specific and nonspecific binding is~7kBT in the DNA Mnt repressor system under our experimental conditions[17].Thus our calculations indicate that secondary binding to sites other than the canonical Mnt repressor site is highly unlikely and can be ignored in our discussion.

1.3 Surface plasmon resonance

The kinetics and equilibrium constants of the protein-DNA interactions were measured by surface plasmon resonance(SPR) using the BIAcoreTM3000(BIAcore AB)at 25℃.The NTA sensor chip surface was initially equilibrated with binding buffer (30 mmol·L-1Tris-Cl,pH 7.5,100 mmol·L-1KCl,0.1 mmol·L-1EDTA,50 g·L-1glycerol,0.005%Tween-20)at a flow rate of 5 μL·min-1.Ni2+was loaded onto the sensor chip surface by injection of 10 μL of 100 mmol·L-1NiCl2in binding buffer.The His6-tagged Mnt-repressor was subsequently immobilized on the chip in binding buffer.To prevent DNA fragments from binding to more than one protein,we applied a very low density of protein(~200 Response Unit(RU))on the chip.DNA dissolved in binding buffer at concentrations from 2.5 to 100 nmol·L-1were injected at a flow rate of 30 μL·min-1.Elution was achieved with buffer containing the same components as the binding buffer,but with a pH of 9.0.

Table 1 Primers used in this study

In order to increase the nonspecific binding and thus obtain a better resolution on nonspecific binding measurement,we decreased the salt concentration to 100 mmol·L-1K+,which is much lower than the estimated intracellular salt concentration of~160 mmol·L-1K+and 5-10 mmol·L-1Mg2+in E.coli[3].

1.4 Kinetic analysis

Kinetic analysis was performed using BIA evaluation 4.1 software(BIAcore AB)according to the manufacturer′s instructions. The results reported here were obtained using the one-step biomolecular association reaction model(1∶1 Langmuir mode), which is described by the equation A+B⇌AB,where A and B represent the DNA fragments and the surface-bound Mnt repressor,respectively.Assuming pseudo-first order interaction kinetics,the rate of complex formation during sample injection is given by d[AB]/dt=ka[A][B]-kd[AB],which is expressed in terms of the SPR signal as dR/dt=kaCRmax-(kaC+kd)R,where dR/ dt is the rate of change of the SPR signal,C is the DNA concentration,Rmaxis the maximum protein binding capacity in RU, and R is the SPR signal in RU at time t,kais the association rate constent,kdis the dissociation rate constant.The dissociation phase is described by dR/dt=-kdR.

2 Results and discussion

The interactions between the Mnt repressor and a variety of DNA fragments were monitored in real time using SPR.All measurements were repeated at least four times for each of the different DNA fragments at different concentrations.

Fig.1 Schematic of the experimental design

2.1 The higher dissociation rate near the end of linear DNA fragments

2.1.1 Experimental results

To investigate whether proteins have a high dissociation rate at the end of linear DNA,we monitored both the association and dissociation of the Mnt repressor with a series of nonspecific DNA fragments of different lengths,ranging from 103 to 503 bp. Our results show that kais linearly proportional to the length of the DNA fragment,kddecreases nonlinearly with DNA length, and the binding equilibrium constant(KA)is linearly proportional to the length of the DNA fragment(Fig.2).

2.1.2 Theoretical analysis

Because Mnt binds a 17-base target sequence,any continuous stretch of 17 bases can theoretically act as a binding target for the Mnt repressor.Since the association rate(or dissociation rate) ofagivenDNAfragmentto(orfrom)theMntrepressoristhesum of all association(or dissociation)probabilities at each position along the DNA,the association rate kaand the dissociation rate kdof a DNA fragment can be expressed as follows:

where konjand koffjdenote the microscopic association and dissociation rates at a given position j,respectively.Ponjand Poffjare the probabilities of efficient collisions and of residence at position j,respectively.N is the number of potential binding sites on the DNA fragment.

(A)If one assumes that the structure of the end has no effect on protein binding,then each position will be equivalent in any one nonspecific DNA fragment,ka,kd,and KAcan be expressed as follows:

where konnonspecificand koffnonspecificare the microscopic association and dissociation rates for one nonspecific binding site,respectively. As for the kd,since the sum of the residence probabilities at each position of a DNA fragmentis always equal to 1,equation (4)will be

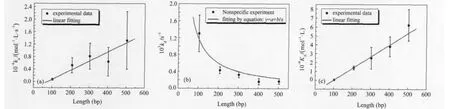
Fig.2 Experimental results with nonspecific DNA fragments(a)length dependence of association rate constant,(b)length dependence of dissociation rate constant,(c)length dependence of equilibrium constant

As a result,

If this is the case,both kaand KAwill be proportional to the number of potential binding sites(the length of the DNA fragment),and kdwill be independent of the length of DNA fragment(Fig.3a).

However,in our experiments,the kdclearly correlated with the DNA fragment length.Therefore,each position should not be equivalent in one nonspecific DNA fragment,and the end structure has some effect on protein binding.

(B)If the structure of the end has some effect on the protein binding at the ends,then there are energetic possibilities.

(a)The end structure influences the activation energy of protein binding at the DNA ends.In this case,the activation energy of the binding reaction at the end position of the DNA fragment will be different from that at internal positions(koninternal≠konend; koffinternal≠koffend),but the free energies of the protein-DNA complex will be the same at different positions(koninternal/koffinternal=konend/koffend). Here koninternaland konendare the microscopic association rate constants for internal and end positions,respectively;whereas koffinternaland koffendare the microscopic dissociation rate constants from internal and end positions,respectively.In order to simplify the analysis,we assume that only the potential binding site closest to the end will be influenced by the end structure.In this case,kaand kdcan be expressed as:

Since the free energy of the binding state at each position is the same in this case,the corresponding residence probability at each position is also the same(1/N).Therefore,equation(7)can be written as:

As a result,

If this is the case,kawill be proportional to the number of po-tential binding sites(the length of the DNA fragment),kdwill be proportional to the reciprocal of the length(1/N),and whether increases or decreases with the length will depend on whether protein dissociation from the end is faster or slower than from internal positions.In addition,KAwill also be proportional to the length of DNA(Fig.3b).

(b)The DNA structure influences the free energy of the DNA-protein complex when the protein is bound at the end.In this case,not only will the konand koffat the end position be different from those at internal positions,but the energy of DNA-protein complex when the protein is bound at the end will also be different from that at internal positions.(koninternal≠konend;koffinternal≠koffend; (koninternal/koffinternal)/(konend/koffend)=eI/eS,where S and I are relative energy differences of protein binding at the end position and at internal positions,respectively.)In this case,ka,kdand KAcan be expressed as follows:

Fig.3 Theoretical changes of ka,kd,and KAas a function of length(a)calculations assume that each position is equivalent for a given nonspecific DNA fragment, (b)calculations assume that the structure influences the activation energy of dissociation from the DNA end position, (c)calculations assume that the structure influences the free energy of the protein-DNA complex when the protein is at the end of the DNA.

If this is the case,kawill be proportional to the number of potential binding sites(the length of the DNA fragment),kdwill be proportional to a function of lengthand whether kdincreases or decreases with the length will depend on whether protein dissociation from the end is faster or slower than from the other positions.In addition,KAwill be proportional to the length of DNA(Fig.3c).

By comparing the theoretical results with experimental measurements,we found that both cases shown in Fig.3b(koffend> koffinternal)and Fig.3c(koffend>koffinternal)agree reasonably well with experiment.Unfortunately,since the difference between the cases shown in Fig.3(b,c)depends on eI-S,which is very difficult to measure,we cannot rule out either of these two possibilities. However,koffend>koffinternalis required for both cases.Therefore,we conclude that end positions are thermodynamically different from internal positions of the DNA fragment during Mnt repressor binding,and the dissociation rate from the end is larger than from internal positions(koffend>koffinternal).

It has been proposed that DNA phosphates located at the ends of DNA fragments bind counterions less effectively than those in the middle of a long DNA strand,and thus experience less counterion displacement upon protein binding[18].This may explain the change in the activation energy or free energy of the binding state at the end position.

In addition,the intersection of the linear fit curve with the xaxis is greater than zero in Fig.2(a,c),suggesting that a minimum DNA length is required for binding by the Mnt repressor.This has also been found in structural studies of the Mnt repressor[19].

2.2 The structure of the ends and the specific binding to the Mnt repressor

To further address whether the structure of the end affects sequence-specific protein binding to a linear DNA fragment even when the binding site is not located at the very end,we measured the binding constant of the Mnt repressor interacting with a variety of DNA fragments containing the specific binding site at either middle or side positions.

First,the equilibrium constant correlated with the length of DNA fragments,as expected,in both Specific-Middle and Specific-Side cases.Nevertheless,for all five different fragments lengths,KAdiffered appreciably between the Specific-Middle case and the Specific-Side case.This strongly suggests that protein bind-ing to DNA is affected by the position of the binding site along the linear DNA fragment(Fig.4(a-c)).

To understand the cause of the position effect,we conducted further theoretical analysis on the DNA binding process.As in equation(11),the binding equilibrium constant of a DNA fragment containing a specific binding site can be expressed as

whereeΔGnonspecificandeΔGspecificnote the relative free energy changes of the nonspecific and specific binding reactions,respectively. Combined with the KAresults from Nonspecific DNA fragments, we obtained an eΔGspecific~(1.5±0.7)×1010/~(5.4±1.1)×109(Specific-Side/Specific-Middle),and an eΔGnonspecific~(1.54±0.78)×107.Here we ignore the end effect,since the difference between specific and nonspecific binding is much larger than the difference between nonspecific bindings at different positions.)

Since eΔGspecificis much larger than eΔGnonspecific,we assume that mostproteinbindsSpecific-Middle/Specific-Side DNA fragments at the specific binding site instead of at the other positions.Then, in principle,the binding process of a Mnt repressor to Specific-Middle/Specific-Side can be divided into two steps:first,the Mnt repressor binds nonspecifically to DNA at any position;second,the Mnt repressor translocates to the specific binding site. Then,the equilibrium binding constant can be expressed as

where KA1middleand KA2middleare the equilibrium constants of the first and second steps for Specific-Middle cases,respectively, KA1sideand KA2sideare the equilibrium constants of the first and second steps for Specific-Side DNA cases,respectively.Since the first step is independent of the specific binding site,KA1middleshould be equal to KA1side.Therefore,the difference between KAmiddleand KAsidereflects the difference between KA2middleand KA2side,indicating a difference in the free energy change of sequence-specific proteinbindingbetweentheSpecific-MiddleandSpecific-Sidecases:

where ΔGmiddleand ΔGsideare the relative free energy changes of the specific binding reaction for the specific-middle and specificside cases,respectively.

To further investigate the length range across which the position effect occurs,we analyzed the differences between Specific-Middle and Specific-Side for five different fragment lengths. Our results show that the differences in free energy change reach a plateau around 300 bp(Fig.4d).As for DNA fragments with the same length,the difference between specific-middle and specificside comes from both ends.The plateau of the difference indicates that the difference at both ends reaches a plateau.Therefore,the position effect ranges from approximately 1-150 bp in our experimental system.

It has been proposed that the binding between the Mnt repressor and the operator can be divided into three steps:(1)bimolecular binding of one dimeric DNA-binding domain to a single operator half-site;(2)intramolecular docking of the second dim-eric DNA-binding domain to the adjacent operator half site;and (3)formation of cooperative contacts between DNA-binding domains[20].The third step relates to DNA bending.This suggests that a likely explanation for the position effect on protein binding to linear DNA is that the lack of rigid structure at the ends of linear DNA may influence the bending of DNA induced during protein binding.

Fig.4 Experimental data for Specific-Middle and Specific-Side DNA fragments(a)length dependence of equilibrium constant,(b)length dependence of dissociation rate constant,(c)length dependence of equilibrium constant, (d)length dependence of the ratio between the equilibrium constants of Specific-Middle and Specific-Side DNA fragments

2.3 The contribution of nonspecific binding sites on equilibrium constants of DNA fragments

From equations(5)and(10),we determined that the difference in KAbetween nonspecific and specific DNA is always given byIn our case,the difference between the Nonspecific case and corresponding Specific-Side case is~(1.5±0.7)×1010mol-1·L,and the difference between the Nonspecific case and corresponding Specific-Middle cases is~(5.4± 1.1)×109mol-1·L.Although the difference is independent of the DNA fragment length,the influence on KAof having a specific binding site on a DNA fragment decreases with the increase in length,as shown in Fig.5.This is because the contribution of nonspecific binding sites will mask the effect of increasing length.

In practice,since the lack of rigid structure at the ends may influence the binding affinity to transcription factors,we should exercise caution when comparing the binding affinities to DNA fragments of different lengths,or to DNA fragments that contain a specific binding site at different positions,especially when one of the DNA fragments contains a binding site near the end.

In some SPR experiments,control channels were loaded with nonspecific DNA fragments of the same length as the experimental fragments.This control binding curve was subtracted from the binding curve for the corresponding experimental DNA fragment in order to calculate the final specific binding curve for further analysis.Given the complexity of nonspecific binding observed in our protein-DNA system,this direct subtraction procedure may not be ideal for isolating sequence-specific binding.

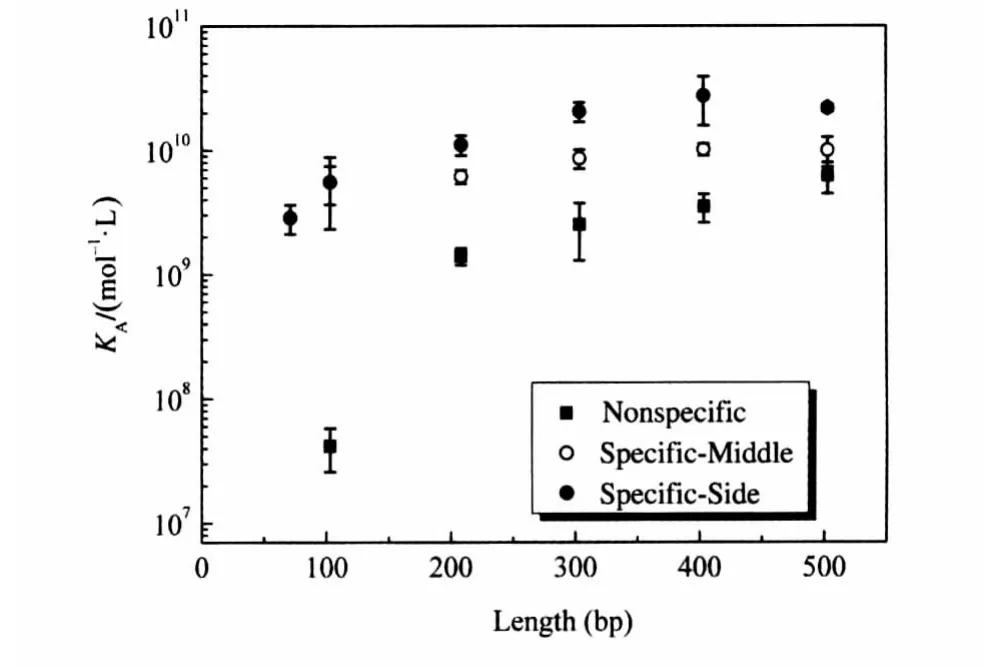
Fig.5 Binding equilibrium constants for Mnt repressor to DNA fragments

3 Conclusions

Using SPR,we monitored both the association and dissociation process of Mnt-repressor with a series of nonspecific DNA fragments.Combined with further theoretical analysis,we clearly conclude that Mnt-repressor dissociation from DNA at the end position is faster than from other positions.In addition, we found that the end can directly influence the protein specific binding when the binding site is too close to the end.

1 von Hippel,P.H.;Rees,W.A.;Rippe,K.;Wilson,K.S.Biophys. Chem.,1996,59:231

2 Halford,S.E.;Szczekun,M.D.Eur.Biophys.J.,2002,31:257

3 von Hippel,P.H.Annu.Rev.Biophys.Biomol.Struct.,2007,36: 79

4 Blainey,P.C.;van Oijen,A.M.;Banerjee,A.;Verdine,G.L.;Xie, X.S.Proc.Natl.Acad.Sci.U.S.A.,2006,103:5752

5 Elf,J.;Li,G.W.;Xie,X.S.Science,2007,316:1191

6 Winter,R.B.;Berg,O.G.;von Hippel,P.H.Biochemistry,1981, 20:6961

7 Winter,R.B.;von Hippel,P.H.Biochemistry,1981,20:6948

8 Vossen,K.M.;Fried,M.G.Anal.Biochem.,1997,245:85

9 Surby,M.A.;Reich,N.O.Biochemistry,1996,35:2209

10 Roberts,R.J.CRC Crit.Rev.Biochem.,1976,4(2):123

11 Jeltsch,A.;Pingoud,A.Biochemistry,1998,37:2160

12 Knight,K.L.;Sauer,R.T.J.Biol.Chem.,1989,264:13706