14族杂环戊二烯分子(硅、锗、锡)的电子结构与光谱性质

邓春梅 牛英利 彭 谦,* 帅志刚,2,*

(1中国科学院化学研究所,北京分子科学国家实验室,有机固体院重点实验室,北京 100190; 2清华大学化学系,北京 100084)

14族杂环戊二烯分子(硅、锗、锡)的电子结构与光谱性质

邓春梅1牛英利1彭 谦1,*帅志刚1,2,*

(1中国科学院化学研究所,北京分子科学国家实验室,有机固体院重点实验室,北京 100190;2清华大学化学系,北京 100084)

14族杂原子取代的杂环戊二烯分子具有独特的光谱性质,成为发光材料的明星分子.为了更深层次地理解硅、锗、锡杂环戊二烯分子的光谱性质,本文从理论上计算了它们的电子结构及其吸收和发射光谱.分别采用密度泛函理论(DFT)和含时密度泛函理论(TD-DFT),优化了硅、锗、锡杂环戊二烯分子基态和第一激发态的平衡构型,计算了电子结构和振动性质.在此基础上,运用振动关联函数公式计算了吸收光谱和发射光谱.得到的吸收光谱和发射光谱,特别是发射光谱的半峰宽与现有的实验值吻合很好.通过分析结构和光谱性质的关系,指出光谱的性质主要取决于苯环转动对应的低频振动模式和中心环C—C键的伸缩振动对应的高频振动模式.

密度泛函理论;14族杂环戊二烯;振动关联函数;光吸收;光发射

Since the discovery of organic light-emitting device(OLED) by Tang and VanSlyke[1],there has been increasing interest in developing highly efficient OLED devices because of their great potential efficient in display,solid-state lighting,and other applications.One of the major current subjects in this field is the development of efficient light-emitting materials.

Group-14 metalloles,silicon-,germanium-,or tin-containing metallacyclopentadienes were first synthesized by Leavitt[2-3]and Braye[4]et al.in 1959-1961.The general structure is of the following form:

where R1and R2could be alkyl,aryl,halides,a second ring,or one or both may be missing.They are so called metalloles due to the metallic nature of the elements M=Si,Ge,Sn.Recently, much attention has been paid to these systems because of their unusual electronic structure[5-6]and exotic aggregation induced emission photophysical characteristics[7]that have made them intriguing candidates for OLEDs.

In general,aggregation quenches luminescence because of either charge transfer or energy transfer or Davydov splitting where dark state becomes the lowest-lying excited state.In contrast,siloles exhibit aggregation enhanced luminescence.Siloles have a quite low-lying LUMO(the lowest unoccupied molecular orbital)level,which is ascribed to the σ*-π*conjugation in the ring,that is,the orbital interaction between the σ*orbital of the two exocyclic σ bonds on the silicon atom and the π*orbital of the butadiene structure[8-9].Siloles exhibit high electron affinity and large electron mobility,which has been employed both as electron-transporting and light-emitting layers for organic electronics[10-11].A recent study showed that the electron mobility of a silole based compound was as much as 100 times higher than that of tris(8-hydroxyquinolinato)aluminum(Alq3),which is widely used as an electron-transport material in OLED[12].Since the intriguing phenomenon,the aggregation-induced emission (AIE),was reported by Tang et al.in 2001[13],a series of silole molecules have been found to exhibit the exotic phenomena and used as excellent light-emitting materials for OLED[14].Recently, germoles and stannoles become subjects of great interest since they display the very similar unusual optical properties as the siloles[5-7].

We have first attempted to understand the AIE phenomena by investigatingtheexcitedstatevibroniccoupling[15-16].Wefoundthe couplings arising from low-frequency nuclear motion contribute the most to the non-radiative decay process.We then developed a fully analytic vibration-correlation function formalism for the internal conversion rate process by considering the multimode mixing(Duschinsky rotation effects).And we further went beyond the“promoting mode”approximation by presenting a formalism which includes all the vibrational modes in the electronic couplings prefactor[17].Eventually,we found that the vibrationcorrelation function formalism can give a comprehensive description for both the radiative and non-radiative decay rates as well as for the optical absorption and emission spectra.

In this work,we present a computational study on the optical absorption and emission spectra for three metalloles,namely, siloles,germoles,and stannoles by using density functional theory(DFT)[18]and time-dependent density functional theory(TDDFT)[19-21]to generate essential electronic and vibrational structures which are eventually coupled with the vibration-correlation function formalism for the optical spectra.For simplicity,these group-14 hexaphenylmetalloles will be referred to the group-14 elements and the substituents:MPh6(M=Si,Ge,Sn).Finally,we will compare the first-principles results with the experiments.

1 Methodology

The absorption spectrum,defined as the rate of energy absorption by a single molecule per unit radiant energy flux,is given by the expression

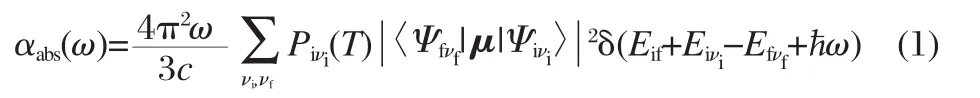
The emission spectrum in photon counting experiments,defined as the differential rate of photon emission due to a single molecule,is

where,Ψiνiand Ψfνfare the molecular wave functions and μ is the electric dipole moment.is the Boltzmann distribution function for the initial state vibronic manifold.c represents the velocity of light and ω represents the vibration frequency.Eif=Ei-Efis the energy difference between the initial and final electronic states.andare the total vibrational energy of the molecule in the initial and final electronic states,respectively.

In the Born-Oppenheimer adiabatic approximation,the wave function of each state can be expressed as a product of the electronic wave function and the wave function for nuclear motion.

μfi=〈Φf|μ|Φi〉,is the electric transition dipole moment,and can be expanded in a Taylor series in the normal coordinates.

For the strongly allowed transitions,the emission is usually dominated by the zero-order term,i.e.,the first term of Eq.(4). While for the weakly allowed or dipole-forbidden transitions, the Herzberg-Teller approximation corresponding to the second term should also be considered.In this paper,we will just consider the zero-order term because the transition between the ground state and the lowest excited state is strongly allowed for all the metalloles,even though our formalism is general.

Applying Fourier transformation,δ(ω)=Then Eqs. (1-2)can be written asis a vibration correlation function of absorption spectrum.(t,T)has the same form as(t,T)with only different initial and final electronic states.

In order to get the fully analytic formalism of Eqs.(5-6),the path integral formula of harmonic oscillator is adopted to derive the Franck-Condon integrals[22-23].Then the final analytic solution of the correlation function could be obtained as

where ai,af,and E are N×N matrices,K is 2N×2N matrix,andare N×1 and 2N×1 matrices,respectively.The details of the correlation function are derived in Ref.[24].

2 Computational details

The molecular equilibrium geometries for the ground state (S0)were optimized at the level of DFT.And the TD-DFT was applied to optimize the first singlet excited state(S1)of the compounds.The B3LYP functional[25]and def2-SV(P)basis set[26]were used,and the effective core potential(ECP)was employed for Sn atom,in particular.There was no symmetric constrain on the geometric optimization.At the equilibrium geometries,the vibration frequencies and the normal modes of S0electronic states were calculated by analytic second derivative calculations,and the ones for S1electronic states were obtained by numerical differentiation of analytic energy gradients.These electronic structure calculations were carried out by using TURBOMOLE 6.0 program package[18,27].Based on the electronic structure information,considering the displaced and distortion of potential energy surface,the absorption and emission spectra of MPh6(M=Si,Ge, Sn)were investigated by means of a home-made program which is described in the Methodology section.

Fig.1 General structure of the group-14 metalloles MPh6 (M=Si,Ge,Sn)

3 Results and discussion

3.1 Ground and excited state geometries

The molecular equilibrium geometries for the S0based on the geometries obtained from the X-ray crystal data[7]were optimized at the level of DFT.The molecular structure is depicted in Fig.1.The selected bond lengths,bond angels,and dihedral anglesofbothS0andS1inMPh6(M=Si,Ge,Sn)arelistedinTable1.

From Table 1,we can find that all three compounds havesimilar conformations in ground state.The three metalloles all have planar central metallol moieties.As for the geometries of the central metallole rings,the heavier metalloles have the longer M—C bond lengths,accompanied with the smaller C2MC5 angles,apparently due to the larger atomic radii of the heavier central group-14 elements.The angles between the phenyl substituents on the diene and the central metallol plane vary from 36.4°to 61.5°,which indicate the two adjacent phenyl rings could not be coplanar with the metallol rings because of the steric hindrance.The substituent phenyl rings give the molecule a propeller-like shape.

Table 1 Selected important bond lengths,bond angles,and dihedral angles of MPh6(M=Si,Ge,Sn)in the ground state and the first singlet excited state

When going from the ground state S0to the first singlet excited state S1,two important geometric modifications should be noted: (1)the bonds C2—C3,C4—C5 are elongated,whereas bonds C3—C4,C2—C20,C5—C50,M—C2,and M—C5 are shortened;(2)the dihedral angles of the phenyl rings at 2 and 5 positions to the central metallole ring dramatically decrease.For these phenomena,the detailed explanation will be given in the next section.

3.2 Molecular orbital calculations

In order to characterize the optical and electronic properties,it is useful to examine the highest occupied molecular orbital (HOMO),the lowest unoccupied molecular orbital(LUMO), and the energy gaps between HOMO and LUMO(Egap).To gain insight into the influence of the heteroatoms in the group-14 metallols on the molecular orbitals,the plots of HOMO and LUMO for group-14 metallols are showed in Fig.2.The calculated HOMO and LUMO energies and the energy gaps are given in Table 2.

As shown in Fig.2,the HOMO and LUMO for all the three compounds displayed qualitatively similar iso-surfaces.The HOMO orbitals resemble the HOMO for cis-butadiene,with some additional contributions from the local HOMO of 2,5-phenyl groups and a lesser extent 3,4-phenyl groups.The LUMO orbitals are similar to the LUMO of butadiene with additional in-phase contributions from a M-Ph σ*orbital and from the local LUMO of the 2,3,4,5-pheneyl groups.Based on the orbitals distribution,we could presume that HOMO levels for these three molecules will be insensitive to the heteroatom while the LUMOlevels will have relations with the heteroatom.The computed data(Table 2)have confirmed this guess.There are slightly increases in the order of SiPh6＜GePh6＜SnPh6both for the LUMO level and the HOMO-LUMO energy gap.The adiabatic excited energy(Ea)between the ground state and the first singlet excited state are also listed in Table 2,and display the same trend as Egap.

Table 2Calculated HOMO and LUMO energies,HOMOLUMO energy gaps(Egap),and the adiabatic excited energy (Ea)for MPh6(M=Si,Ge,Sn)

In general,the HOMO orbitals exhibit bonding character and the LUMO orbitals antibonding character.Since the first singlet excited state corresponds almost exclusively to the excitation from the HOMO to the LUMO in all the studied compounds,we could predict the differences of the bond lengths between the S0and S1from MO nodal patterns.For example,the HOMO orbitals of the studied molecules are bonding across the C2—C3, and C4—C5 bonds,whereas the LUMO orbitals have nodes in these regions.The calculated results in Table 1 are in agreement with this anticipated elongation of these bonds.On the contrary, the HOMO orbitals have nodes across the C3—C4,C2—C20, C5—C50,M—C2,and M—C5 bonds,while the LUMO orbitals are bonding in these regions.Therefore,the bond lengths of these bonds become considerably shorter in the excited state as discussed in the previous section.

3.3 Absorption and emission spectra

Based on the electronic structure information,the absorption from S0to S1and emission from S1to S0spectra for the three compounds are calculated and depicted in Fig.3(a,b).And the comparison between the calculated absorption and emission spectra and the experimental ones[10]of SiPh6are shown in Fig.4. In addition,the maximum absorption and emission peak positions,the full width at the half maximum(FWHM),and the available corresponding experimental data of each molecule are listed in Table 3.

Fig.2 Calculated HOMO and LUMO for the group-14 metalloles MPh6(M=Si,Ge,Sn)

Compared with the experimental data,lower excited energies are always obtained by using TD-DFT method due to the limitation of inherent electron self-interaction in DFT methodologies. Furthermore,the experimental data are detected in the acetonitrile solution,while the computed data are obtained in gas phase by employing a single molecule.Therefore,when compared with the experimental data,both the absorption and emission spectra exhibit red shifts(seen in Table 3).And in Fig.4,in order to compare the lineshape of the calculated spectra with the experimental ones[10],we move the calculated spectra to the higher energy scale(3102 cm-1in absorption spectra and 1883 cm-1in emimission spectra)to make sure the maximum peaks overlap. From Fig.4,it can be seen that the lineshapes of the calculated spectra,which stem from the coupling between electronic excited state and the vibration mode,agree excellently with the experimental ones.These indicate that our thermal vibration correlation function method works well for the MPh6molecules. For the absorption spectrum,it is need to note that the transition only from S0to S1is calculated,while in the experimental measure the absorption spectrum includes the transition not only from S0to S1but also from S0to the second singlet excited state S2.

Fig.3 Absorption(a)and emission(b)spectra of the group-14 metalloles MPh6(M=Si,Ge,Sn)

Fig.4 Comparisons of the calculated absorption(a)and emission(b)spectra of SiPh6with the experimental ones

Table 3 The maximum peaks(λ)and full widths at the half maximum(FWHM)of absorption and emission spectra

Due to the distortion effect of harmonic potential energy surface,i.e.,different frequencies for the ground and the first singlet excited states,a mirror image relation does not appear between the absorption and emission spectra.For absorption spectra,we find that these three molecules have similar lineshapes,and the FWHM of the absorption spectra have a slight increase in the order of SiPh6＜GePh6＜SnPh6.For emission spectra,the emission maximum wavelength of GePh6is the shortest(529 nm)while thoseofSiPh6andSnPh6arecomparableto each other(547 vs 549 nm),this trend agrees well with the experimental results[76],and the FWHM of the emission spectra also have a slight increase in the order of SiPh6＜GePh6＜SnPh6.For SiPh6,the FWHM of the calculated emission spectra is in excellent agreement with the experimental one[10](3861 vs 3847 cm-1).

From the schematic descriptions of displaced and distortion potential energy surfaces of two electronic states in Fig.5,it is very easy to understand that the characteristics of absorption or emission spectra are determined completely by the adiabatic excited energy between two electronic states(discussed in the last section),molecular reorganization energy of the finial state,and the photon distribution(ni=1/(eħωi/kT-1))of the initial state.Here the temperature effect is not discussed and all the spectra are calculated at 300 K,so we will focus on the analysis of the molecular reorganization energies in the following.

Fig.5 Schematic description of displaced and distortion potential energy surfaceEv1and Ev2represents the vertical excited energy under the geometry structure of the first singlet excited state and that of ground state,respectively.Ereorg.1and Ereorg.2are the reorganization energy of the ground state and the first excited state, respectively.

For a normal mode i,its reorganization energy Ereorg.iis the productofthe Huang-Rhys factorof the normal mode and the corresponding vibration energyand thetotalreorganizationenergyisthesumof

Table 4 and Table 5 give the selected vibration frequencies (cm-1)with important reorganization energies of these three molecules in the first excited and the ground states.For the absorption spectra,the data in Table 4 tell us that for the three compounds the main contributors to the reorganization energies with large values always appear in the high frequency modes(with frequencies 1240－1550 cm-1)and the low frequency ones(with frequencies ca 60 and 90 cm-1).And for emission spectra,as shown in Table 5,the modes with the high frequency(ca 1519 and1565cm-1)andlowfrequency(≤70 cm-1)contribute the most to the reorganization energies for these three molecules.To both absorptionand emission spectra,the former(high frequency modes)are assigned to the single-bond and double-bond stretching vibrations of carbon-carbon related to the central metallole ring, and the latter(low frequency modes)belong to the rotation motions of free phenyl rings at 2 and 5 positions of central metallole ring.

We further project the reorganization energies onto the internal coordinates of the molecules.In general,the potential energy surface can be expanded with internal coordinates around the equilibrium geometry.

where V0is the potential energy at the equilibrium geometry,siand sjrepresent the variation of redundant internal coordinates from the equilibrium geometry,and Fi,jis expansion coefficient. Let′s set V0=0 as the zero point of the potential energy surface. Then,

where,

It should be noted that Viincludes the contribution,fromthei-thinternalcoordinateandthecouplingterm,from the i-th and j-th internal coordinates.

Table 4 Selected vibration frequencies(ωe)of the first excited state and the reorganization energies(Ereorg.2)of the group-14 metalloles MPh6(M=Si,Ge,Sn)

Table 5 Selected vibration frequencies(ωg)of the ground state and reorganization energies(Ereorg.1)of the group-14 metalloles MPh6(M=Si,Ge,Sn)

Table 6 Component of reorganization energy in the selected internal coordinate representation

Selected internal coordinates with large component of reorganization energy are listed in Table 6.The data in Table 6 tells us that it is very obvious that the contribution to the reorganization energy mainly come from the stretching vibration of these bonds (C2—C3,C3—C4,C4—C5,C2—C20,C5—C50)and the rotation motions of the free aromatic rings at the 2 and 5 positions of central ring,which is fully consistent with the structure change from the ground to the excited state,discussed in Section 3.1. Nevertheless,all the data demonstrates that there are no noticeable contribution to the optical properties directly coming from the heavy elements Si,Ge,and Sn.

4 Conclusions

The electronic structures and spectra properties of a series of group-14 metalloles,from silole to stannole,have been studied with vibration correlation functions method coupled with DFT and TD-DFT computations.The HOMO′s and LUMO′s for all the three compounds are found to dominate the electronic excited state and to possess qualitatively similar isosurfaces.The three molecules have similarly optical lineshapes,while the full width at the half maximum(FWHM)of both the absorption and emission spectra have slightly increases in the order SiPh6＜GePh6＜SnPh6.Both the lineshapes of the calculated optical absorption and emission spectra,especially the FWHM for all the compounds at room temperature,were in good agreement with the available experiments.The excited state vibronic couplings are revealed by projecting the reorganization energies into both normal mode and internal coordinate components.Both the lowfrequency modes assigned to rotation motion of the free aromatic rings and the high-frequency modes from carboncarbon stretching motions are found to contribute importantly to the optical spectra features such as the bandwidth broadening.

Acknowledgment:Itisourgreathonorwiththisworktocelebrate the 100th anniversary of College of Chemistry and Molecular Engineering,Peking University,the 100 years full with glory.Fruitful discussions with Professors Eli Pollak(Department of Chemical Physics,The Weizmann Institute of Science),Jiushu Shao(Department of Chemistry,Beijing Normal University),and Qiang Shi(Institute of Chemistry,Chinese Academy of Sciences)are greatly acknowledged.

1 Tang,C.W.;VanSlyke,S.A.Appl.Phys.Lett.,1987,51:913

2 Leavitt,F.C.;Manuel,T.A.;Johnson,F.J.Am.Chem.Soc.,1959, 81:3163

3 Leavitt,F.C.;Manuel,T.A.;Johnson,F.;Matternas,L.U.; Lehman,D.S.J.Am.Chem.Soc.,1960,82:5099

4 Braye,E.H.;Hubel,W.;Caplier,I.J.Am.Chem.Soc.,1961,83: 4406

5 Yamaguchi,S.;Itami,Y.;Tamao,K.Organometallics,1998,17: 4910

6 Yamaguchi,S.;Endo,T.;Uchida,M.;Izumizawa,T.;Furukawa, K.;Tamao,K.Chem.Eur.J.,2000,6:1683

7 (a)Ferman,J.;Kakareka,J.P.;Klooster,W.T.;Mullin,J.L.; Quattrucci,J.;Ricci,J.S.;Tracy,H.J.;Vining,W.J.;Wallace,S. Inorg.Chem.,1999,38:2464 (b)Tracy,H.J.;Mullin,J.L.;Klooster,W.T.;Martin,J.A.;Haug, J.;Wallace,S.;Rudloe,I.;Watts,K.Inorg.Chem.,2005,44:2003 (c)Mullin,J.L.;Tracy,H.J.;Ford,J.R.;Keenan,S.R.;Fridman, F.J.Inorg.Organomet.Polym.Mater.,2007,17:201

8 Khabashesku,V.N.;Balaji,V.;Boganov,S.E.;Nefedov,O.M.; Michl,J.J.Am.Chem.Soc.,1994,116:320

9 Tamao,K.;Yamaguchi,S.Pure Appl.Chem.,1996,68:139

10 Zhan,X.;Risko,C.;Amy,F.;Chan,C.;Zhao,W.;Barlow,S.; Kahn,A.;Bredas,J.L.;Marder,S.J.Am.Chem.Soc.,2005,127: 9021

11 Chen,J.;Law,C.C.W.;Lam,J.W.Y.;Dong,Y.;Lo,S.M.F.; Williams,I.D.;Zhu,D.;Tang,B.Z.Chem.Mater.,2003,15: 1535

12 Murata,H.;Malliaras,G.G.;Uchida,M.;Shen,Y.;Kafafi,Z.H. Chem.Phys.Lett.,2001,339:161

13 Luo,J.D.;Xie,Z.L.;Lam,J.W.Y.;Cheng,L.;Chen,H.Y.;Qiu, C.F.;Kwok,H.S.;Zhan,X.W.;Liu,Y.Q.;Zhu,D.B.;Tang,B. Z.Chem.Commun.,2001:1740

14 Hong,Y.;Lam,J.W.Y.;Tang,B.Z.Chem.Commum.,2009: 4332

15 Yu,G.;Yin,S.W.;Liu,Y.Q.;Chen,J.S.;Xu,X.J.;Sun,X.B.; Ma,D.G.;Zhan,X.W.;Peng,Q.;Shuai,Z.G.;Tang,B.Z.;Zhu, D.B.;Fang,W.H.;Luo,Y.J.Am.Chem.Soc.,2005,127:6335

16 Yin,S.W.;Peng,Q.;Shuai,Z.G.;Fang,W.H.;Wang,Y.H.;Luo, Y.Phys.Rev.B,2006,73:205409

17 Niu,Y.;Peng,Q.;Shuai,Z.G.Sci.China Ser.B-Chem.,2008,51: 1153

18 Treutler,O.;Ahlrichs,R.J.Chem.Phys.,1995,102:346

19 Bauernschmitt,R.;Ahlrichs,R.Chem.Phys.Lett.,1996,256:454

20 Bauernschmitt,R.;Häser,M.;Treutler,O.;Ahlrichs,R.Chem. Phys.Lett.,1997,264:573

21 Grimme,S.;Furche,F.;Ahlrichs,R.Chem.Phys.Lett.,2002,361: 321

22 (a)He,Y.;Pollak,E.J.Phys.Chem.A,2001,105:10961 (b)He,Y.;Pollak,E.J.Chem.Phys.,2002,116:6088

23 (a)Ianconescu,R.;Pollak,E.J.Phys.Chem.A,2004,108:7778 (b)Tatchen,J.;Pollak,E.J.Chem.Phys.,2008,128:164303

24 Peng,Q.;Niu,Y.L.;Deng,C.M.;Shuai,Z.G.Chem.Phys.,2010, accepted

25 Becke,A.D.J.Chem.Phys.,1993,98:1372

26 (a)Schafer,A.;Horn,H.;Ahlrichs,R.J.Chem.Phys.,1992,97: 2571 (b)Weigend,F.;Ahlrichs,R.Phys.Chem.Chem.Phys.,2005,7: 3297

27 Ahlrichs,R.;Baer,M.;Haeser,M.;Horn,H.;Koelmel,C.Chem. Phys.Lett.,1989,162:165

December 16,2009;Revised:January 25,2010;Published on Web:February 25,2010.

Electronic Structures and Spectroscopic Properties of Group-14 Metalloles MPh6(M=Si,Ge,Sn)

DENG Chun-Mei1NIU Ying-Li1PENG Qian1,*SHUAI Zhi-Gang1,2,*
(1Key Laboratory of Organic Solids,Beijing National Laboratory for Molecular Sciences,Institute of Chemistry,Chinese Academy of Sciences,Beijing 100190,P.R.China;2Department of Chemistry,Tsinghua University,Beijing 100084,P.R.China)

Group-14 metalloles possess interesting optical properties and are promising molecules for light-emitting materials.We present a theoretical study of the electronic structures and the optical spectra from silole to stannole to gain insight into their optical properties.The optimized equilibrium geometries and the electronic and vibrational structures for the ground state(S0)and the first singlet excited state(S1)were calculated using density functional theory (DFT)andtime-dependentdensity functional theory(TD-DFT),respectively.The optical absorption and emission spectra were calculated using the thermal vibration correlation function formalism.The lineshapes of the calculated optical absorption and emission spectra,especially the full width at half maximum for all the compounds at room temperature, were found to be in good agreement with the available experimental data.Low-frequency modes that are assigned to the rotation motion of free aromatic rings and the high-frequency modes related to the stretching vibration of carboncarbon bonds contribute greatly to the optical features such as the bandwidth of the optical line-shapes.

Density functional theory; Group-14 metalloles; Vibration correlation function; Optical absorption; Light emission

*Corresponding authors.Email:qpeng@iccas.ac.cn,zgshuai@tsinghua.edu.cn;Tel/Fax:+86-10-62797689.

The project was supported by the National Natural Science Foundation of China(90921007)and National Key Basic Research Program of China(973) (2009CB623600).

国家自然科学基金重大项目(90921007)和国家重点基础研究发展计划项目(973)(2009CB623600)资助

帅志刚,北京大学化学与分子工程学院兼职教授.

O641