提高采样频率实现随机共振用于高频信号检测

张良斌

(襄樊学院 机械与汽车工程学院，湖北 襄樊 441053)

提高采样频率实现随机共振用于高频信号检测

张良斌

(襄樊学院 机械与汽车工程学院，湖北 襄樊 441053)

针对随机共振仅适合于低频信号的约束，对随机共振技术运用于强噪声背景下的高频信号检测进行研究，提出提高采样频率的方法，使高频信号变换成低频信号. 数值仿真表明，此方法检测单频信号效果显著，检测调幅信号是有效的.

随机共振；采样信号；采样频率；调幅信号

近20年来，在许多自然科学领域，随机共振的理论和实验成果得到了广泛的应用. 在机械工程中，可以应用随机共振来检测机械故障[1-5]. 但随机共振已有的理论仅适用于低频率、低噪声的小参数信号. 为了利用随机共振实现较高频率微弱信号的检测，文献[6, 7]提出了调制随机共振方法，通过振幅调制和频率调制产生易发生随机共振的低频分量，通过双稳系统产生随机共振；文献[8]提出尺度变换方法、文献[9]提出二次采样方法，将较高频率信号变换为较低频率信号从而实现利用随机共振检测高频信号的目的. 本文研究用提高采样频率的方法实现将高频信号变换为低频信号，通过双稳系统产生随机共振.

1 提高采样频率实现随机共振的原理

非线性双稳系统在单频信号 a sin(2π ft)和高斯白噪声ζ(t)作用下的动力学方程为

式(1)中，a是被检测微弱周期信号的振幅；f是被检测弱周期信号的频率；ζ(t)是背景噪声，统计性质为ζ(t) =0， ζ( t )ζ(t ′)= 2D1δ(t). 由于式(1)的复杂性，目前没有分析解，只能用微分方程数值解法，通常采用四阶Runge-Kutta算法对式(1)进行数值计算，如下式

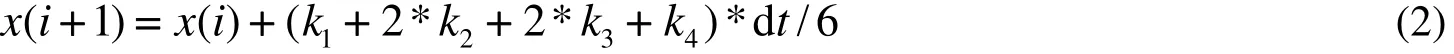
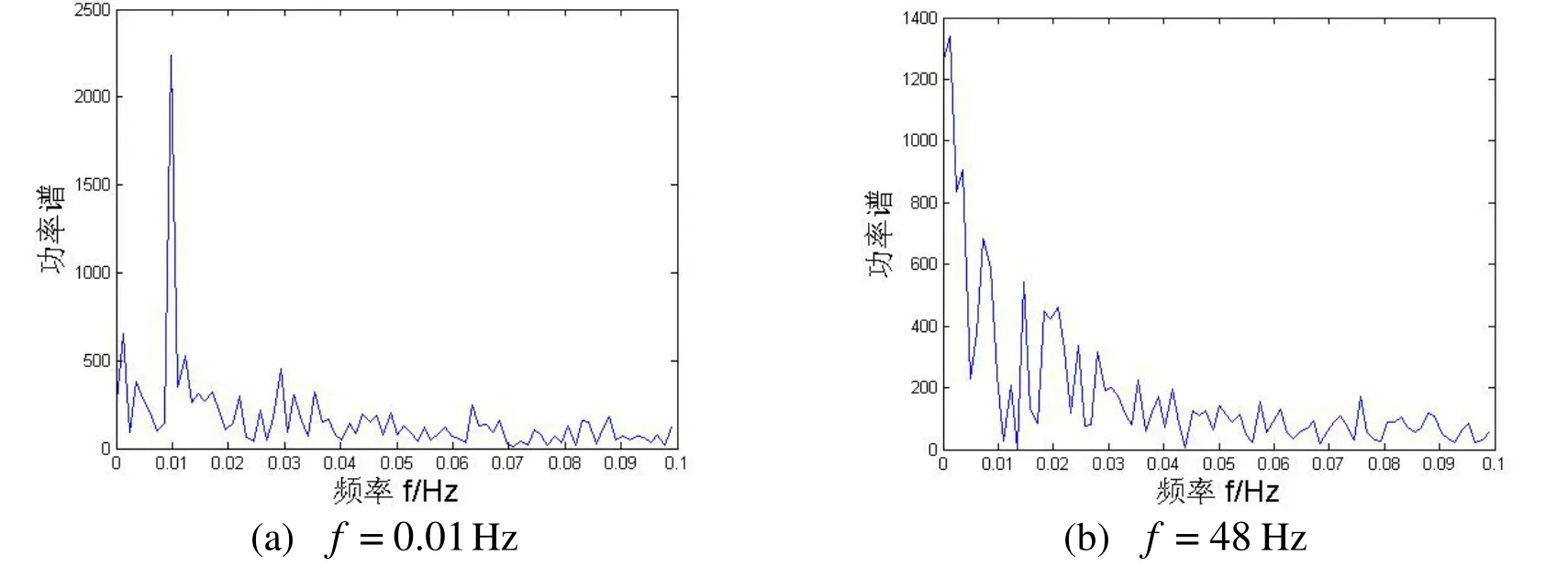
图1 式(2)的输出频谱图 μ=1, a= 0.3, D1=0.5

事实上，在实际检测中首先对有背景噪声的被测信号 s( t) =a sin(2π ft) + ζ采集数据，输入双稳系统的是离散时间信号，被测信号可以由它的采样信号精确恢复. 对周期信号 a sin(2π ft)采样的结果是把连续时间信号变成离散时间信号，如果信号频率f=48Hz，对其进行采样的采样频率 fos=n⋅ f= 24000，采样周期是采样点数取4096的信号曲线如图2(a)所示. 如果采集的4096个采样值不变，把采样周期增大到迭代步长采样值间距增大了倍，信号曲线如图2(b) 所示.从图2(a)和图2(b)直观地看出，采样点数和采样值都不变，采样值间距增大n′倍，周期信号频率缩小n′倍，从48Hz缩小到0.01Hz.

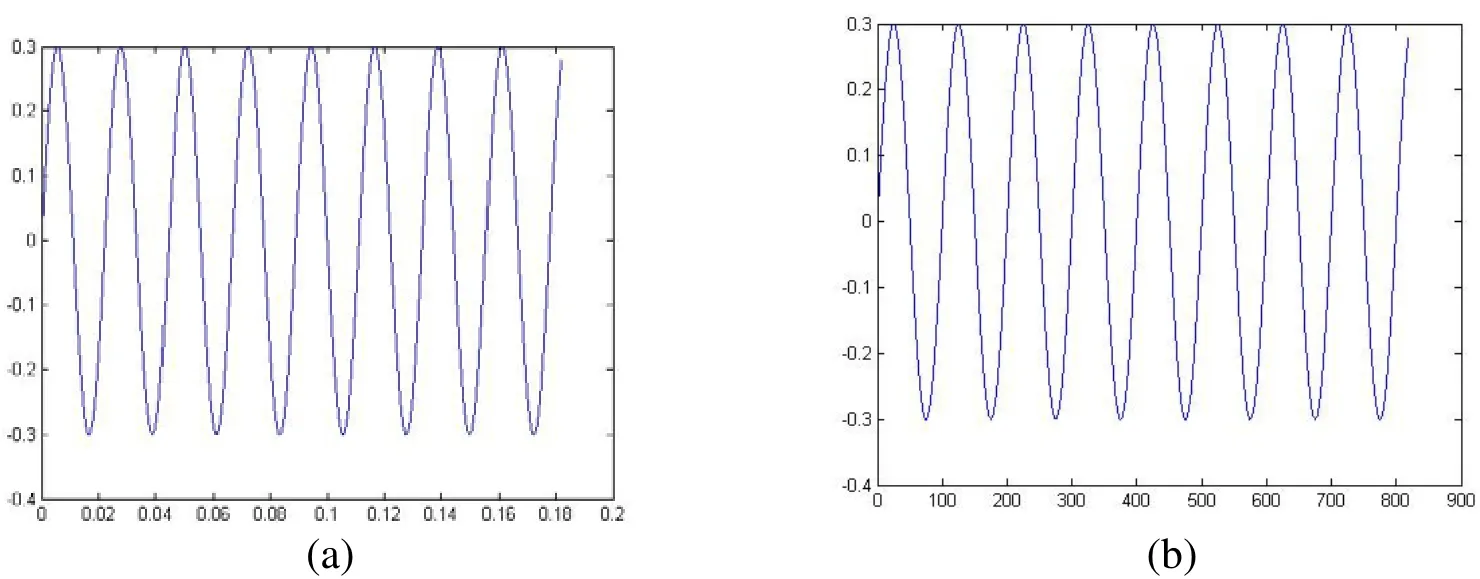
图2 不同采样值间距的信号

受此启发，可以利用这种频率变换方法把高频信号换成低频信号后输入双稳系统，以便产生适合于随机共振的低频信号.

2 数值仿真

设被测信号频率f=50Hz，由采样频率计算公式得到fos=n⋅ f=25000，将4096个采样数据输入双稳系统进行数值计算时应在式(2)前加采样信号：

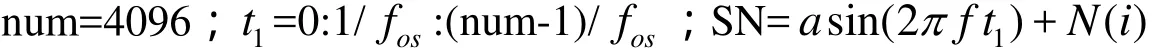
式(2)中的 a *sin(2* PI* f*(t + dt/ 2)) + N( i )换成 SN，迭代步长不变. 采样值间距增大了n′= dt ⋅fos=5000倍，输出频谱图如图3所示，从图3看出D1=0.5时在频率0.01处出现明显的谱峰，D1大于和小于0.5峰值都减小. 实际频率可以按比例还原， f = 0.01 × n′= 50Hz.

在实际中常遇到被检测信号与其他频率的信号产生调制的现象，设被检测微弱信号 a sin(2π f2)的振幅被一固有信号调制后成为调幅信号 a cos(2π f1t ) i cos(2π f2)，把此调幅信号和背景噪声直接输入双稳系统的动力学方程为

其中， sn( t) =a cos(2π f1t ) i cos(2π f2t)+ζ，a是被检测微弱信号的振幅，f2是被检测信号的频率，f1是被检测信号的调制频率，ζ(t)是被测信号的背景噪声. 例如f1=70，f2=20，调幅信号可展开成

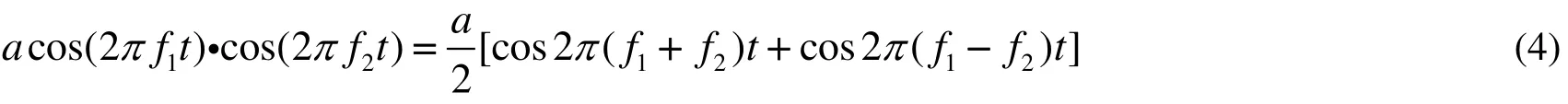
其中，f1+f2= 90，f1−f2= 50.

对 sn( t)采集数据，采样频率 fos= 500 × 50=25000，把SN换成调幅信号后数值计算的输出频谱图如图4所示. 从图4看到有两个明显峰值，大峰值按比例还原实际频率是0.01× n′=50Hz，小峰值按比例还原实际频率是0.018 × n′=90Hz，由式(4)可以得出f1和f2的频率. 如果被测信号是两个单频信号相加的混合信号，也可用此法测频率.

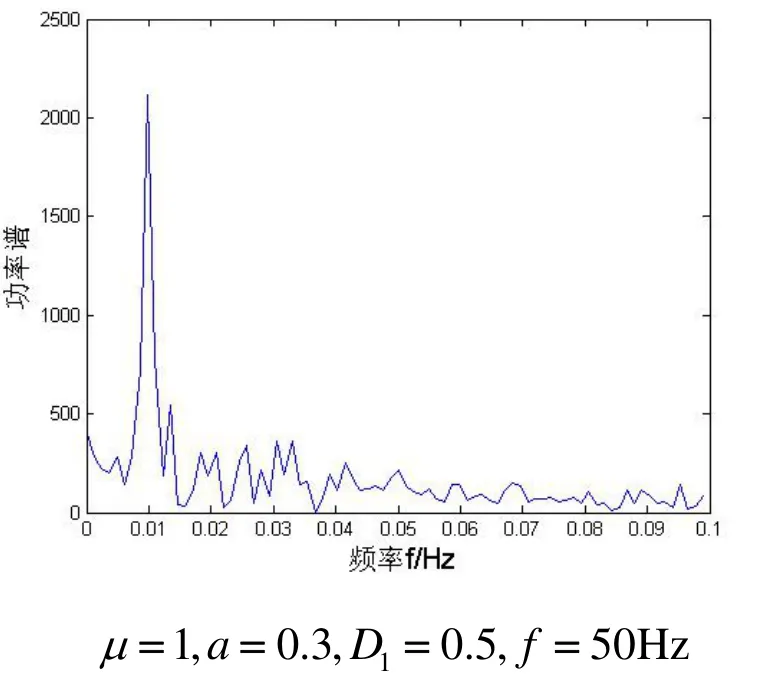
图3 采样信号的输出频谱图

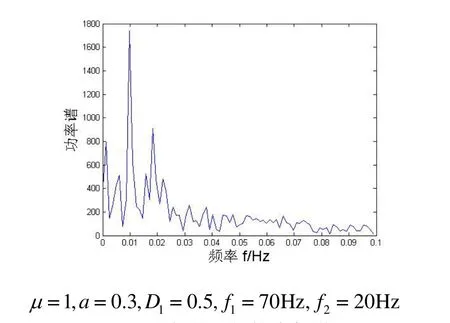
图4 调幅信号的输出频谱图

3 结语

本文分析了采样信号的采样频率和被测信号频率之间的关系，针对随机共振仅适合于低频信号的约束，提出了用提高采样频率的方法实现高频信号随机共振. 通过数值仿真表明，此方法在检测高频微弱信号方面具有有效性和优越性，也可检测调幅信号和混合信号，为微弱信号检测问题提供了良好的解决途径.

[1] ZHANG LIANGYING, CAO LI, WU DAJIN, et al. Stochastic resonance in linear regime of a single-mode laser[J]. Chinese Physics Letters, 2003, 20 (1): 25-27.

[2] BERDICHEVSKY V, GITTERMAN M. Stochastic resonance in linear systems subject to multiplicative and additive noise[J]. Physical Review, 1999, 60(2):1494-1499.

[3] 肖方红, 闫桂荣, 韩雨航. 双稳随机动力系统信号调制噪声效应的数值分析[J]. 物理学报, 2004, 53(2): 0396-0400.

[4] 祝恒江, 李 蓉, 温孝东. 利用随机共振在强噪声下提取信息信号[J]. 物理学报, 2003, 52 (10): 2404-2408.

[5] 扬定新, 胡茑庆. 随机共振在微弱信号检测中的数值仿真[J]. 国防科技大学学报, 2003, 25 (6): 91-94.

[6] 林 敏, 黄咏梅. 基于调制随机共振的转子故障早期检测[J]. 中国电机工程学报, 2006, 26 (8): 128-131.

[7] 张良斌, 张良英. 基于频率调制随机共振的弱周期信号检测[J]. 噪声与振动控制, 2008, 28 (3): 17-20.

[8] 范胜波, 王太勇, 冷永刚, 等. 基于变尺度随机共振的弱周期性冲击信号的检测[J]. 中国机械工程, 2006, 17(4): 387-390.

[9] 冷永刚, 王太勇. 二次采样用于随机共振从强噪声中提取弱信号的数值研究[J]. 物理学报, 2003, 52(10): 2432-2437.

(责任编辑：饶 超)

To Detect High-frequency Signals with Stochastic Resonance by Improving Sampling Frequency

ZHANG Liang-bin
(School of Mechanical and Automotive Engineering, Xiangfan University, Xiangfan 441053, China)

High-frequency signal detection under heavy noise background by using random resonance technology was studied. Random resonance technology only applied to detect very low-frequency signals, the method of increasing the frequency of sampling was proposed, which could turn high-frequency signals into low-frequency signals. The numerical simulation shows that this method not only detects single-frequency signals well, also detects AM signals well.

Stochastic resonance; Sampling signal; Sampling frequency; AM signal

TM307

A

1009-2854(2010)02-0039-03

2010-01-10；

2010-01-29

湖北省教育厅重点科研基金项目(D200725001)

张良斌(1959— ), 男, 湖北襄樊人, 襄樊学院机械与汽车工程学院讲师.