基于数字形态学的角点检测算法研究

方 磊 ，杨建强

(襄樊学院 数学与计算机科学学院，湖北 襄樊441053)

基于数字形态学的角点检测算法研究

方 磊 ，杨建强

(襄樊学院 数学与计算机科学学院，湖北 襄樊441053)

给出了一种利用数学形态学来提取数字图像中的角点且能够区分凸角中角点和凹角中角点的方法. 此方法与Harris角点方法通过实验比较，形态学角点算法不会依赖于要找角点数量的给定值，并且可以分别找出凹角上的点、凸角上的点这两类不同的角点，深化了对图像的描述和理解.

数学形态学；图像角点；凸角点；凹角点

角特征是数字图像的一种重要局部特征，它在图像匹配、目标描述与识别等领域都有重要应用[1]. 现有的检测方法分为两类：1)根据图像边缘特征，用轮廓点来计算边缘曲率或夹角来判定角点；2)直接利用灰度信息进行角点检测. 但是，这些方法要么依赖于前期对图像分割处理的结果，要么对噪声敏感，精度较低.

1 常用的角点检测方法

常用的角点检测有SUSAN角点检测[2]. 用圆形模板在图像上移动，若模板内像素的灰度与模板中心像素灰度的差值小于一定阈值，则认为该点与中心像素具有相同或相近的灰度，由满足这样条件的像素组成的区域称为“USAN”( Univalue Segment Assimilating Nucleus). 当圆形模板在图像上移动时，“USAN”区域面积不断变化，角越尖锐面积越小. 如果以一种特定的面积为阈值，那么可以得到不同尖锐程度的角点. 该方法依赖于阈值的选择，不能描述图像的角点是凹角上点还是凸角上的点.

Harris角点检测[3]是常用角点检测方法之一，但也存在测算出的角点太多，包含不具有较强特征点的问题，同样也不能描述和区分凹角上点，凸角上的点. Harris角点检测中灰度图像I( x, y)在点(x, y)处的梯度

M矩阵是二阶实对称矩阵，因此，必然存在2个特征值α、β，当点(x, y)的评价函数R值大于某一阈值时，这个点就是一个角点，一般取值为0.04~0.06.

Harris方法确定的角点的评价函数为

2 数学形态学的凸区域中角点和凹区域中角点的提取算法

2.1 数学形态学算子[4-6]

数学形态学的语言是集合论，数学形态学的基本运算为腐蚀和膨胀，它们是一对对偶运算. 因此可以说，数学形态学的基本运算只有一个，即腐蚀或膨胀. 开运算、闭运算是通过腐蚀或膨胀来定义的.

对于二值图像，设集合A为二值图像，集合B为结构元素. 膨胀运算为A⊕B，腐蚀运算为AΘB.

2) 闭运算： A• B = (A ⊕ B )Θ B 闭运算也能平滑图像，它能去掉原图像中的小洞，填补轮廓上的小缝隙并能融合图像上狭窄的缺口. 由于膨胀和腐蚀的对偶性，开运算和闭运算也可得到相应对偶性.

对于灰度图像，设灰度图像为函数f，结构元素为函数k，那么灰度图像的膨胀和腐蚀表示如下.

这里Df、Dk分别是f，k的定义域，平移参数x−i，y−j必须在f的定义域内.

2.2 基于形态学方法对图像特征区域的定位设灰度图像为函数f，结构元素为函数k.

尖峰提取算子(1)可检测图像中的波峰. 由于开运算可以平滑图像轮廓，除去图像中细小突出、图像中的某些狭长部分或两个对象之间连接的小桥，所以尖峰提取算子能提取出图像的凸区域. 低谷提取算子(2)是(1)的对偶算子，可检测图像中的波谷. 由于闭运算能平滑图像，可去掉原图像中的小洞，填补轮廓上的小缝隙并能融合图像上狭窄的缺口，所以低谷提取算子能提取出图像中的凹特征区域. 尖峰和低谷提取算子(3)可同时检测到图像的波峰和低谷.

由以上三个算子提取的区域是图像灰度发生剧烈变化的区域，而角点也是出现在图像灰度剧烈变化的区域，所以图像的角点一定会出现在特征区域中. 因此先提取特征区域可以减少角点的提取范围，提高提取角点的精度，减少计算量.

2.3 凸角点和凹角点提取算法

通过2.1和2.2的分析，结合SUSAN角点检测方法，给出凸角点和凹角点具体提取算法如下：

算法1，凸角点的提取.

Step 1：对图像用形态学算子(1)提取波峰图像I，定位图像的凸区域；

Step 2：对Step 1得到的图像I，找出它的灰度的动态范围 T= fmax− fmin，t=0.3*T；

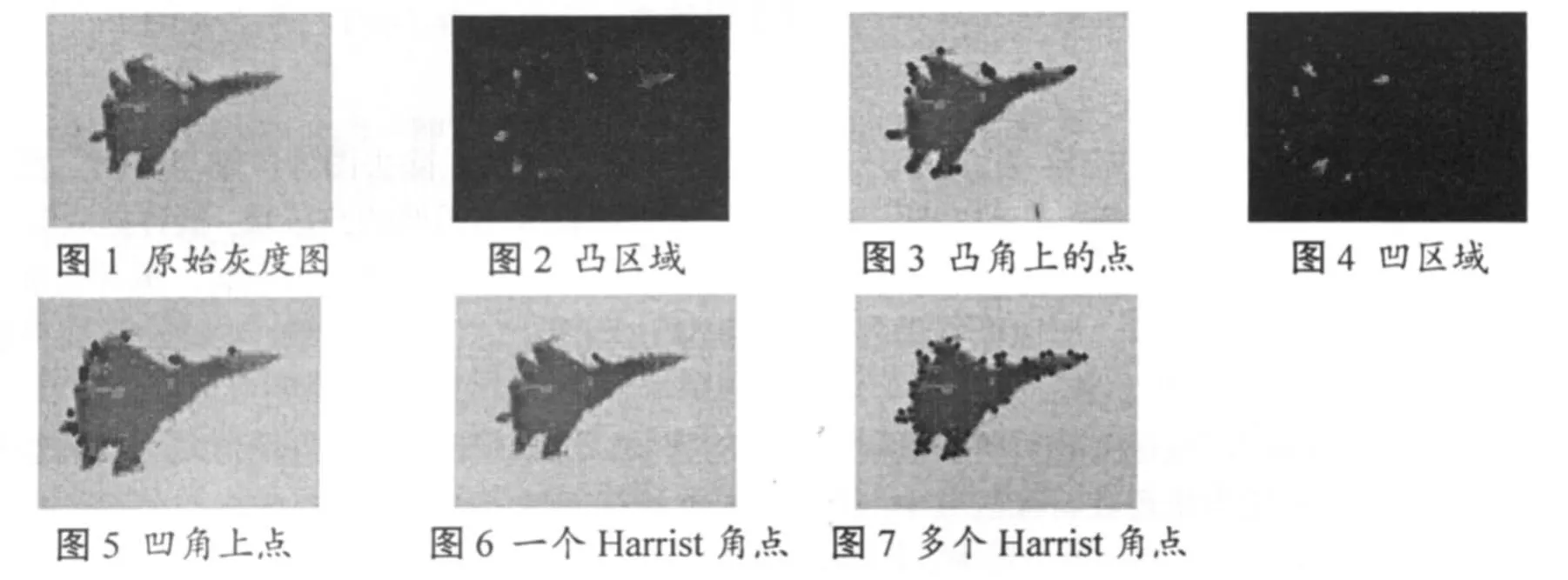
Step3：对图像I上每个点(x, y)，统计它的邻域模板M(p,q)中满足不等式|I( i, j) − I( x, y) |

Step 4：对N进行判断，若 N=(p* q )/2，则说明点(x, y)在边缘直线上，若 N<(p* q )/2，则说明点(x, y)处于一个角上，提取该点，并且当N越小，该角越尖锐. 根据应用需求给定一个表示角的尖锐程度的判别值λ， λ< (p* q)/2. 当 N<λ，点 (x, y)即是尖锐程度为λ时的一个角点.

算法2，凹角点的提取.

Step 1：对图像用形态学算子(2)提取波谷图像I，定位图像的凹区域；

Step 2：对Step 1得到的图像I，找出它的灰度的动态范围 T= fmax− fmin，t=0.3*T；

Step 3：对图像I上每个点(x, y)，统计它的邻域模板M( p, q)中满足不等式 |I(i ,j)−I(x,y )|

Step 4：对N进行判断，若 N= (p* q )/2，则说明点(x, y)在边缘直线上，若 N<(p* q )/2，则说明点(x, y)处于一个角上，提取该点，并且当N越小，该角越尖锐. 根据应用需求给定一个表示角的尖锐程度的判别值λ， λ< (p* q)/2. 当 N<λ，点 (x, y)即是尖锐程度为λ时的一个角点.

算法1与算法2的不同之处在Step 1中，两者的特征区域提取公式不同.

3 实验分析

图1 为待处理的原始灰度图像，图2是使用算法1中形态学算子对图1处理后得到的凸区域，定位了凸区域就使角点的搜索限制在更小的范围之内，并且确定的角点的位置特性只会在凸区域中搜索，而不会在凹区域上搜索. 使用算法1对图1进行处理最终得到图3. 图3中点是提取到的角点. 可以看出在图3中提取了图像上主要的凸角上的点，而没有凹角上的点.

图4是使用算法2中形态学算子对图1处理后得到的凹区域，定位了凹区域就使角点的搜索限制在更小的范围之内，并且确定的角点的位置特性只会在凹区域中搜索，而不会在凸区域上搜索. 使用算法2对图1进行处理最终得到图5. 图5中的点是提取到的角点. 可以看出在图5中提取图像上主要的凹角上的点，而没有凸角上的点.

使用Harrist 角点方法对图1进行处理，当指定提取一个角点时得到图6，当指定提取40个角点时得到图7，由此可见Harrist角点方法依赖于提取点数的选择. 存在的问题是在提出取角点之前，一般并不知道会有多少个角点. 在图5中，尖锐的点找出来了，比较平滑部位不很尖锐的点也提取出来，并且不能区分是凹角上的点还是凸角上的点.

4 结语

由上述的实验结果可以发现：1)数学形态学方法可以分别找出凹角上的点，凸角上的点. 对图像的性质给了一个更详细的描述，而在现有的其它角点方法中，均达不到它的简单、定性的效果. 2)Harris 方法提取角点，依赖于给定一个指定的点数，如果这个指定的点数不切合实际情况，则会把没有明显特征的点也找出来. 与Harris 方法相比，形态学算子不会依赖于要找点数的给定值，因此基于数学形态学的角点提取算法具有独特的优越性.

[1] 张坤华, 王敬儒, 张启衡. 多特征复合的角点提取方法[J]. 中国图像图形报: A版, 2002, 7(4): 319-324.

[2] SMITH S M, BRADY J M. 一种新的对低灰度级图像处理的苏姗方法[R]//Delence Research Agency. Internal Technical Report TR95SMSI. Chobham Lane hertsey Surry, UK, 1995.

[3] HARRIS C, STEPHENS M. 一种角点和边缘检测方法[C]// 4thAlvey Vision Conference. Plessey, UK: [出版者不详], 1988: 147-151.

[4] 龚 炜, 石青云, 程明德. 数字空间中的数学形态学: 理论及应用[M]. 北京: 科学出版社, 1997.

[5] 崔 屹. 图像处理与分析: 数学形态学方法及应用[M]. 北京: 科学出版社, 2000.

[6] 吴敏金. 图像形态学[M]. 上海: 上海科学技术文献出版社, 1991.

(责任编辑：陈 丹)

Research on Corner Detection Algorithm Based on Mathematical Morphology

FANG Lei, YANG Jian-qiang
(School of Mathematical & Computer Sciences, Xiangfan University, Xiangfan 441053, China)

A method with which corner in digital image can be obtained and convex corner and concave corner can be distinguished from each other. Compared with Harris corner algorithm, this method do not depend on the given corner number and can find convex corner and concave corner respectively, deepening the description and understanding to the image.

Mathematical morphology; Corner in image; Convex corner; Concave corner

TP391.41

A

1009-2854(2010)02-0032-03

2010-01-05;

2010-01-26

方 磊(1970— )，女，湖北通山人，襄樊学院数学与计算机科学学院讲师.