多小波基多尺度多传感器数据融合
2010-12-07任亚飞柯熙政
任亚飞,柯熙政
(西安理工大学自动化与信息工程学院,陕西西安710048)
0 引言
众所周知,傅里叶分析中的基函数e±iω是唯一的,而小波变换的基函数却不是唯一的,满足一定条件的函数均可作为小波基函数。小波分析方法的一个突出优点在于小波基的多样性,不同的小波基往往具有不同的时频特性,能够有效地表示一个信号的不同部分或不同特征。信号和噪声经过小波分解后,各尺度的系数分布情况会影响到去噪结果,而小波基的选取又在一定程度上影响着分解后的小波系数分布。因而,小波基选取的好坏直接影响到信息去噪的效果。
小波变换本身固有的特性使得它在数据处理中有着其他方法难以比拟的优势,小波变换已被越来越多的学者们应用到多传感器的数据融合中。尽管利用小波变换融合效果比较好,但在融合的过程中仍存在2个问题,即小波基函数的选择和最佳小波分解层数的选取。在融合规则相对固定的情况下,选择合适的小波基将是改善数据融合效果的有效途径。通过对小波基时频特性的分析比较并结合数据融合的实例,从数据融合结果的统计特性出发,得出了选择合适小波基的方法。有关最佳小波基的选取问题,一直是小波分析应用中的一个难题,目前还没有形成一个统一的标准。现有的小波去噪方法一般都是选用单个的小波基,很难兼顾实际信号中存在的不同类型噪声。鉴于此,本文提出了一种新的基于多个小波基的多尺度多传感器数据融合方法。
1 MEMS噪声描述
1.1 MEMS 噪声
MEMS信号具有高稳定频率源的特点,经过研究表明其相对频率偏差量的随机起伏,主要包含5种独立噪声的线性组合,这些独立的噪声频率谱密度可如下表示

式中α=-2,-1,0,1,2;0<f<fh;hα为常数,随测量设备的不同而存在差异;fh为测量系统的高端截止频率;α根据取值的不同,分别代表5种不同的噪声:α=-2为频率随机游走噪声,α=-1为调频闪烁噪声,α=0为调频白噪声,α=1为调相闪烁噪声;α=2为调相白噪声。在MEMS中这5种噪声分别表现为量化误差、角随机游走、角速率随机游走、零偏不稳定性和速率斜坡。
MEMS陀螺仪的零偏稳定性是表征陀螺仪性能的重要参数,是角速率数据中的低频零偏波动,主要体现在f-1噪声上,该类噪声属于“闪烁调频噪声”,其来源主要是MEMS中的电路组件和环境噪声,还有其他可能产生随机闪烁的部件。其存在使得频率源的随机起伏过程并不平稳,也就是说,它的概率分布是随时间的延续而改变的。在闪烁调频噪声存在的情况下,源信号序列发散,此时的标准方差也随每组量测次数的增加而增大。另外,若使用标准方差来表示零偏稳定性,首先需要假定MEMS信号源的频率随机起伏是一种平稳的随机过程,其概率分布呈正态分布,这才可以用标准方差来表征该信号源的频率稳定度,但这种假设在f-1噪声存在的情况下是不成立的。对于MEMS来说,如何快捷可靠地测得其零偏稳定性,是它走向市场需要解决的问题。目前利用传统的标准方差来测试的方法,由于需要长时间反复的测试,对于测试的惯性转台来说不可能连续几天或者更长的转动,一方面会引入热噪声;另一方面,也会给测试周期带来不利的延迟。
1.2 Allan 方差
David Allan于1966年提出了Allan方差,最初该方法是用于分析振荡器的相位和频率不稳定性。由于陀螺等惯性传感器本身也具有振荡器的特征,因此,该方法随后被广泛应用于各种惯性传感器的随机误差辨识中。Allan方差的基本原理如下:
设系统采样周期为τ0,连续采样N个数据点y(i),i=1,2,…,N。对任意的时间 τ =mτ0,m=1,2,…,N/2,由式(2)求取该族时间内各点的均值序列Y(k),由式(3)求取差值序列D(K),即

普通Allan方差的定义如式(4)

其中,〈〉表示取均值,p=1,2,…,Round((N/m)-1)
Allan方差反映了相邻2个采样段内平均频率差的起伏。它的最大优点在于对各类噪声的幂律谱项都是收敛的;此外,每组测量N=2,大大缩短了测量的时间。本文采用Allan方差对MEMS的误差进行分析和建模,MEMS陀螺随机漂移的Allan均方差分布如图1。
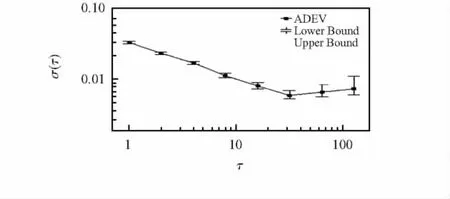
图1 MEMS陀螺随机漂移Allan方差Fig 1 Allan variance of MEMSgyro random drift
2 小波域数据融合
2.1 多尺度分解
小波多尺度模型的主要优点:1)细尺度上的细节信号对应的方差比较大,这说明由此模型产生的随机信号在细尺度上的细节信息的不确定性较高,因此,在进行信号的状态估计或重构的过程中,在给定的误差范围内,可以不考虑相关细尺度上的小波系数。2)同尺度上的小波系数是独立同分布的,不同尺度上的小波系数的分布是相似的。因此,由该模型建立起的随机过程具有自相似性,即分形特征,而自然界的许多现象或过程大都具有分形特征,所以,利用模型将能很好地刻画这些现象或过程。3)多尺度先验模型既可以正则化病态逆问题,同时又可以把先验信息综合到目标信号的估计中。常用的融合规则有很多种,实验中在每个层上基于各只传感器的小波熵进行局部最优的融合估计,最后得到基于全局信号的融合估计值。基于小波变换的多尺度多传感器融合方法如图2,图3所示。
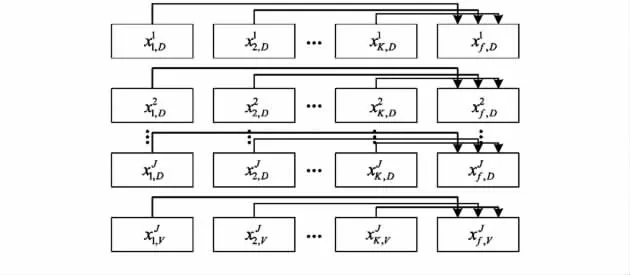
图2 分层数据融合Fig 2 Data fusion on scale

图3 小波逆变换得到融合结果Fig 3 Fusion results obtained by wavelet inverse transform
2.2 多小波基融合
在小波分解中,目前的小波基函数主要分为正交小波、半正交小波、双正交小波等几类。不同的小波基主要具有紧支撑、对称正则度、消失矩等不同的性质。在小波的应用中,小波基的选取可以从一般性原则和具体对象两方面进行考虑。一般性原则有:正交性源于数学分析的简单和工程应用中的便于理解操作;紧支集可以保证有优良的时频局部特性,也有利于算法的实现;对称性则关系到小波的滤波特性是否具有线性相位,这与失真问题密切相关;平滑性则关系到频率分辨率的高低。
另外,考虑使用对象,对于MEMS传感器的信号,要实际问题实际分析。根据上面分析的MEMS的噪声描述,企图用单个小波基把它很好地表示出来是很困难的。本文提出了一个简单但非常有效的基于多个小波基的融合去噪方法,其算法具体流程如图4。
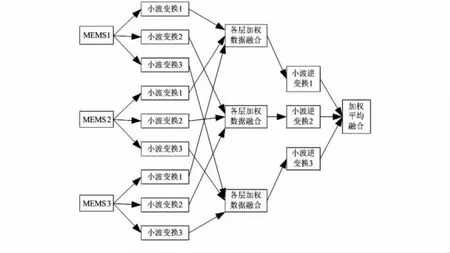
图4 基于多小波基分解的融合过程Fig 4 Fusion based on multi-wavelet base decomposition
基于小波多尺度分解,以2只传感器的融合为例,对于多小波基多传感器的融合方法可由此类推,融合的基本步骤如下:
1)先选择n个具有不同性质的小波基,分别对含有噪声的传感器原始数据进行多尺度小波分解,将问题放到多尺度空间中处理;
2)基于各个传感器的观测信息,在不同尺度上得到目标信号分解到该尺度上的小波系数和最粗尺度上的尺度系数的估计值;
3)对各分解层分别进行多传感器的融合处理时,各分解层上的不同频率分量,即每个尺度上的目标信号的小波系数和最粗尺度上的尺度系数,可采用相同或不同的融合规则进行融合处理,最终得到融合后各层上的小波系数;
4)融合规则选择,考虑MEMS的噪声情况,利用Allan方差作为权值进行加权融合;
5)最后对各层上融合后的小波系数进行小波逆变换,在最细尺度上所得到的重构数据,为基于不同小波基的多尺度多传感器融合结果;
6)再将这些结果做简单的加权平均处理,即为融合后的目标信号。
选取的小波基的数目n一般来说,数目越多,去噪效果越好,但计算量也随之增大,不利于工程实现。
3 实验
实验中,选择对MEMS陀螺仪的零偏稳定性进行研究,目的是利用多个MEMS陀螺仪的数据在小波域进行数据融合,希望提高融合后输出结果的零偏稳定性。由于MEMS陀螺仪零偏稳定性是对零输入下输出结果的均方差表述,各传感器的均值是MEMS陀螺仪零偏稳定性的平均值,反映MEMS陀螺仪的性能。若标准差大,则传感器数据分布分散,MEMS陀螺仪的零偏稳定性弱;标准差小,MEMS陀螺仪的零偏稳定性强。
各种小波基数据融合结果如表1,可以看出:haar,bior,coif小波基都对MEMS有相对较好的处理效果,本文选择这3种小波基对三路MEMS的原始信号进行多小波基多尺度多传感器的数据融合实验,如图5。实验结果表明:融合后不但使零偏数据在零附近具有很高的概率,而且还相对集中,零偏稳定性得到了较大的提高。
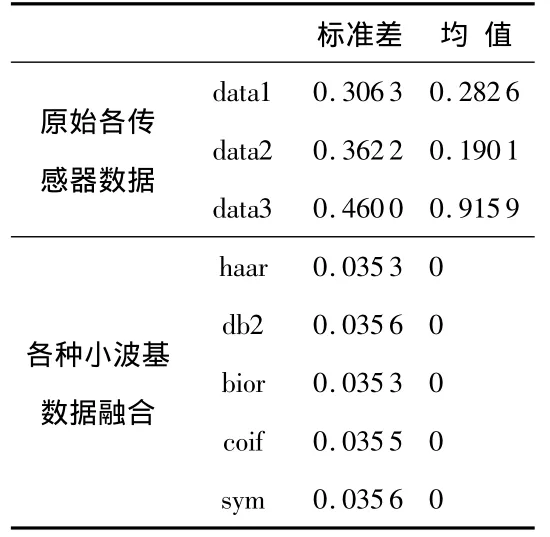
表1 各种小波基数据融合结果Tab 1 Data fusion results of multi-wavelet base
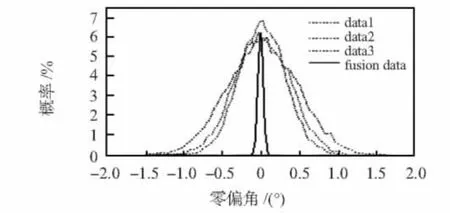
图5 概率分布图Fig 5 Probability distribution diagram
4 结论
小波已经广泛地应用在数据处理的各个领域,但由于小波基函数的选取目前还没有形成统一的标准和原则,在实际应用中,可以采用多小波基数据融合的方法来处理问题。实验证明:结合多尺度多传感器数据融合技术,多小波基数据融合这种方法不仅简单易行,而且能达到很好的效果。
[1]程 坚,王敬东.李 鹏.SAR与可见光图像融合中小波基选择的研究[J].红外技术,2008,1(3):158-163.
[2]龚昌来.多个小波基联合的多聚焦图像融合方法[J].激光与红外,2008,38(11):1156-1160.
[3]申晓华,艾 宝,王 婷.多聚焦图像融合中小波基函数选取的研究[J].弹箭与制导学报,2007,27(3):231-235.
[4]徐国荣,刘金涛.基于多小波基的医学图像融合[J].图像分析,计算机应用与技术,2009(8):112-115.
[5]秦定宇,王敬东,李 鹏.图像融合中小波基的选择分析[J].光电子技术,2006,26(3):203-208.
[6]李庆武,倪 雪,石 丹.一种采用多个小波基的图像融合去噪方法[J].光电工程,2007,34(11):103-108.
[7]柯熙政,任亚飞.多尺度多传感器融合算法在微机电陀螺数据处理中的应用[J].兵工学报,2009,30(7):994-998.
[8]任亚飞,柯熙政.基于阿伦方差的微机电陀螺误差建模及其粒子滤波[J].中国计量学院学报,2009,20(2):102-106.
