杂质不完全离化对MISiC气体传感器的影响*

王 巍，代作海，王晓磊，唐政维，徐 洋，王 平

(1.重庆邮电大学 光电工程学院，重庆400065;2.重庆邮电大学自动化学院，重庆400065)

0 引言

金属—绝缘体—碳化硅(metal-insulator-SiC，MISiC)结构的气体传感器具有耐高温、易于集成、响应速度快等特点，在汽车电子、军事工业以及航空航天等领域都具有广泛的应用前景［1～3］。而SiC材料中杂质离化能较大，因而，杂质离化程度受温度的影响较大，在常温条件下，SiC器件中的杂质元素不能完全离化。而杂质的离化程度又与器件的电学特性有着密切的关系。因此，杂质不完全离化现象对MISiC传感器的性能有很大的影响。

许多学者对SiC中杂质不完全离化对器件影响进行了研究。Lades M等人［4］的研究表明:杂质不完全离化现象会明显地影响SiC器件的瞬态开关特性。Raynaud C等人［5］的研究表明:杂质不完全离化会引起SiC MOS结构的C-V曲线移动和Kink效应的出现。一般情况下，对于SiC的不完全离化问题的处理是基于半导体中的准中性条件，其中杂质的离化能取为恒定值。这种方法在解决SiC内中性区杂质的不完全离化问题时是准确的。当有电场存在时，电场会造成杂质离化能的降低，就无法利用常规方法对SiC空间电荷区中的杂质离化进行分析。

本文在全面考虑影响SiC中杂质离化因素的基础上，对6H-SiC中杂质的不完全离化进行了分析，研究了电场对杂质离化的影响，在MISiC空间电荷区运用电中性条件，对泊松方程进行数值计算，得到了MISiC器件的I-V和C-V特性。

1 SiC中杂质的不完全离化现象

SiC中杂质的离化能可以在较大范围内变化。杂质元素占据的晶格(六方或立方)替位格点不同，所具有离化能也各不同。为了计算电离杂质的浓度，对于施主杂质，可用下式表示离化杂质和掺杂浓度之间的关系［7］

式中 Nd为掺杂的施主浓度，N+d为离化的施主浓度，gd为施主杂质能级的基态简并因子，对于施主型杂质，取gd=2;n为电子浓度，k为玻尔兹曼常数，T为温度，Nc为导带有效状态密度，定义为

由于杂质在SiC中可能占据不同格点，其对应的离化能也不同，以n型6H—SiC为例，则式(1)应改写为

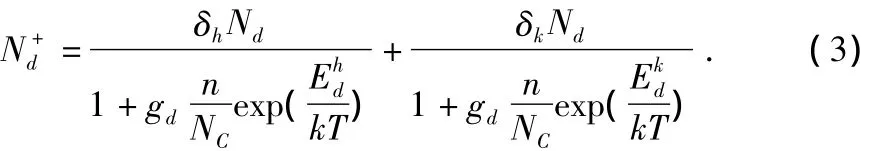
式(3)是关于载流子浓度的超越方程，使用数值方法可以得到杂质电离浓度与掺杂浓度之间的关系，如图1所示。

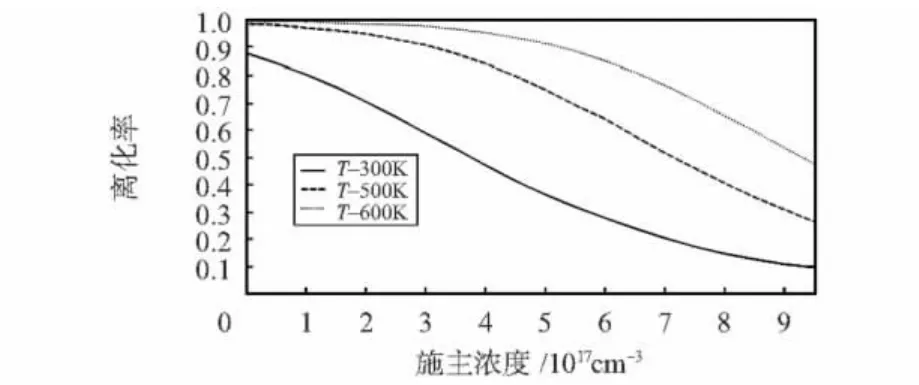
图1 不同温度下杂质离化率和掺杂浓度关系图Fig 1 Relation diagram of dopant ionization ratio vs doping content at different temperature

由图1可知，室温下杂质并未完全离化，在相同温度条件下，掺杂浓度越大，则离化率越小。在同样的掺杂浓度条件下，随着温度的升高，杂质离化率也随之增大，当掺杂浓度≤3×1017cm－3，温度上升到600 K时，杂质才几乎完全离化。但较高的掺杂浓度需在更高温度下才能完全离化。

2 外加电场对杂质离化的影响

由于受Poole-Frenkel效应的影响，杂质离化能一般会降低［8］。如果忽略外加电场对杂质离化能的影响，则可以得到离化能降低量ΔE的表达式为

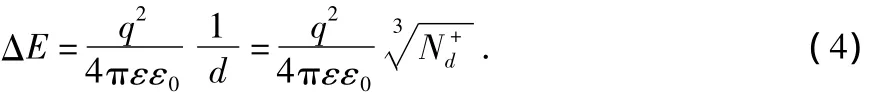
当有外加电场时，杂质离化能的降低量ΔE为［9］

其中，E0为外加电场。

由式(5)可以得知，杂质离化能的降低量与外加电场有关。外加电场增大将导致杂质离化能的降低，从而使得杂质离化率增加。在外加电场作用下，6H-SiC中施主离子的离化能变为

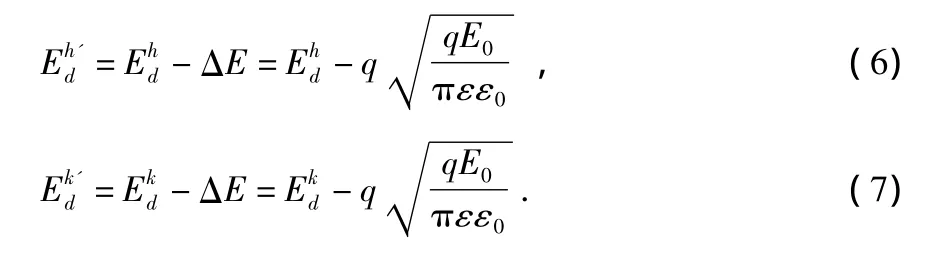
将式(6)和式(7)代入式(3)中，可以求出不同电场下n型6H-SiC离化率和温度的关系，以及不同掺杂浓度下MISiC空间电荷区杂质的离化浓度随位置变化关系，如图2和图3所示。

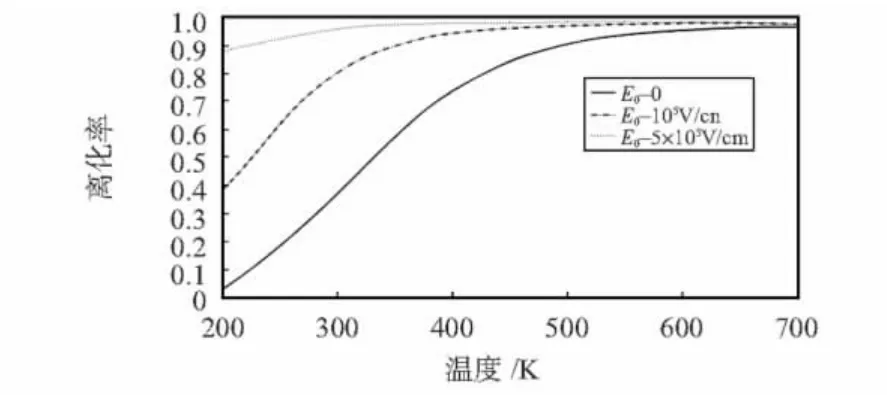
图2 电场对SiC杂质离化率的影响Fig 2 Influence of electric field on dopant ionization

由图2可知，电场会使杂质的离化能降低，从而引起杂质的离化率增强。同时可以看出:在其他条件相同的情况下，随着温度的升高，杂质的离化率逐渐增大，与图1得出的结论一致。

图3所示为在室温时，在电场作用下的空间电荷区杂质离化分布图。由图可知，当掺杂浓度较高时，电场对杂质离化的影响要比在掺杂浓度低时大得多。也就是说在高掺杂情况下，电场对MISiC器件的杂质离化影响将增大。而空间电荷区电场只会使杂质离化能降低，降低杂质的不完全离化效应，但不能完全消除不完全离化效应。

以下对MISiC器件的电势分布进行分析。假定衬底为n型半导体，则空间电荷区的泊松方程为

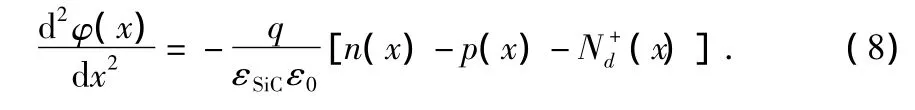
根据玻尔兹曼分布，空间电荷区的载流子浓度如下式

考虑到空间电荷区电场的影响，杂质的离化能会减小，则式(3)应该改为

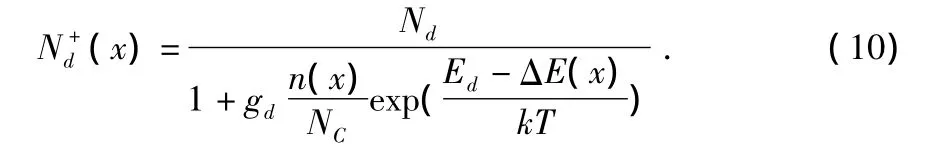
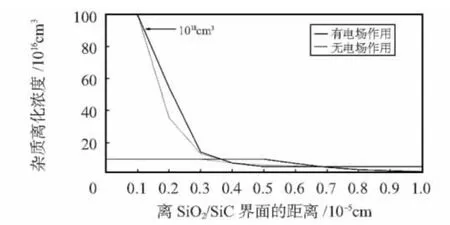
图3 空间电荷区杂质离化分布Fig 3 Dopant ionization distribution in space charge region

其中，ΔE(x)为电场作用下杂质电离能的降低量，由式(5)可得

对处于室温下的MISiC器件来说，由于低温时本征载流子浓度少子无法在短时间内产生，因此，可以忽略不计算，因此，泊松方程变为

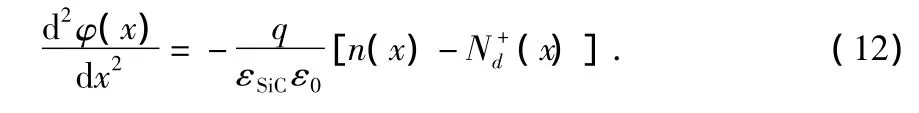
为了对空间电荷区的电势分布做进一步的分析，需要求解泊松方程式。可采取数值方法对其进行求解［5］。首先将划分n个等效网格，并设第i个网格点的坐标为Xi，网格间距为hx，利用二阶求导公式有

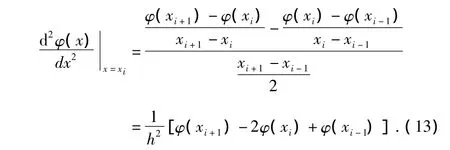
结合式(12)和式(13)，则有

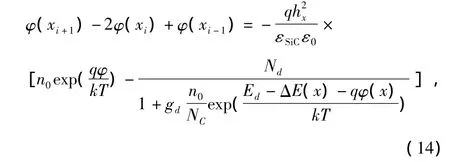
式中 i=1～n。

使用叠代法对式(14)进行求解，可以得到空间电荷区电势φ的分布。图4中所用到的条件为:表面势为0.5 V，掺杂浓度为1.0×1018cm－3，温度为室温。从图中可以看到，在杂质完全离化的情况下，耗尽区宽度变窄，而SiC中杂质的不完全离化使得电势在SiC中的变化放慢，使耗尽区加长，这相当于在杂质完全离化的情况下，掺杂浓度变小。外加电场的存在使得杂质的离化率增大，电势分布曲线由于电场的存在而向杂质完全离化的方向靠近。尚也淳等人的结果还表明:在表面势较低和掺杂浓度较高时，电场的影响更明显，电场最终还会导致C-V曲线的移动［10］。

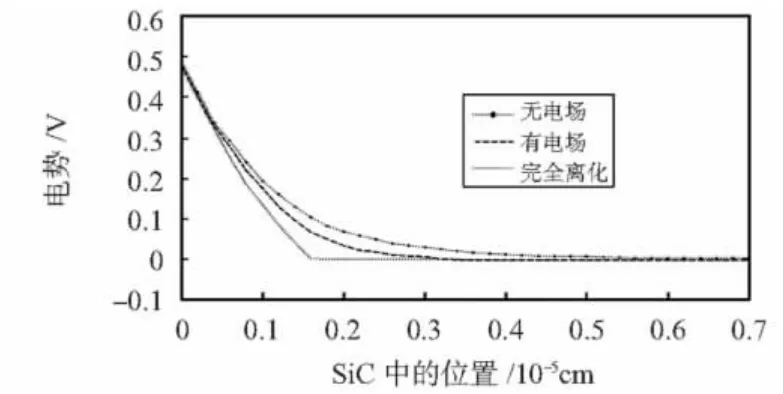
图4 空间电荷区的电势分布Fig 4 Potential distribution in space charge region

3 杂质离化对传感器特性的影响

利用文献［9］提供的参数，得到杂质离化率，进而可以得到如图5所示的电流密度随电压变化关系曲线。可以看到，在低温时，杂质不完全离化对器件的影响比较显著，因为在低温下，杂质中有部分载流子被冻结，杂质离化率很低。而只有在温度大于600 K左右时，杂质已基本全部离化，才不需要考虑杂质离化对器件性能的影响。这说明了在低温下常规半导体器件模型不再适用于SiC器件，这与图2仿真结果相吻合。

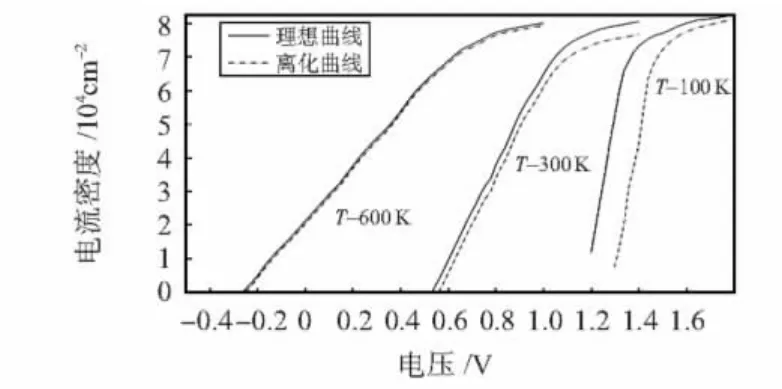
图5 MISiC器件电流密度随电压的变化关系图Fig 5 Relation diagram of current density vs voltage

MISiC器件的C-V特性曲线如图6所示。仿真条件为:温度为300 K，杂质浓度取1017cm－3，不考虑界面态的影响。结果表明:空间电荷区中电场的作用会引起器件C-V特性的移动，使得其电容值较无电场时略微增大。这是因为在电场作用下，杂质的离化率会增大，使得越来越多的离化杂质离子聚集在空间电荷区。同时可以看出:电场离化作用使得器件电容在电压3V处，向下弯曲形成一个小尖，并且，电容随后随着栅压的增大而成递增趋势。Raynaud C［5］称其为KinK效应，是由SiC器件中杂质的不完全离化现象所引起的。

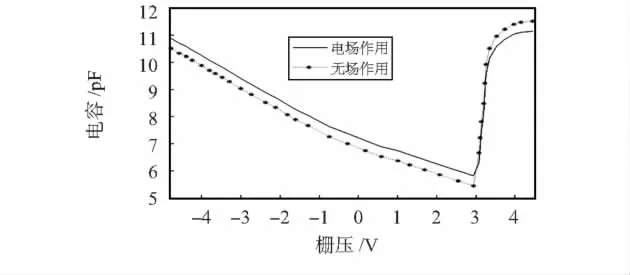
图6 MISiC器件的低频C-V曲线图Fig 6 Curve of capacity vs voltage at low frequency

4 结束语

本文从杂质不完全离化和外加电场两方面入手，建立了MISiC空间电荷区泊松方程。通过对电中性和泊松方程的数值求解，研究了MISiC电特性。仿真结果表明:室温下SiC中部分载流子被冻结，杂质不完全离化，随着温度的升高，杂质离化率增大。在外加电场的作用下，杂质的离化率增大，电势分布曲线向杂质完全离化的方向靠近。导致MISiC器件I-V与C-V曲线的移动，从而使得MISiC气体传感器的灵敏度发生变化。

［1］Kim C K，Lee JH，Choi SM，et al.，Pd and Pt-SiC Schottky diodes for detection of H2and CH4at high temperature［J］.Sensor and Actuator B，2001，77(1):455－462.

［2］Gurbuz Y，Kang W P，Davidson JL.Analyzing the mechanism of hydrogen adsorption effects on diamond based MiShydrogen sensor［J］.Sensors and Actuators B，1996，35(1－3):68－72.

［3］Casady J B，Johnson R W.Status of silicon carbide(SiC)as a wide-band gap semiconductor for high temperature applications:A review［J］.Solid State Electronics，1996，39(10):1409－1422.

［4］Lades M，Kaindl W，Kaminski N，et al.Dynamics of incomplete ionized dopants and their impact on 4H/6H SiC devices［J］.IEEE Trans.Electron devices，1999，46(3):598－604.

［5］Raynaud C，Autran J L.Theoretical investigation of incomplete ionization of dopants in 6H-SiCmetal oxide semiconductor capacitors［J］.J Appl Phy，1999，86(4):2232－2236.

［6］郝 越，彭 军.杨银堂.碳化硅宽带隙半导体技术［M］.北京:科学出版社，2000.

［7］刘恩科，朱秉升，罗晋生.半导体物理学［M］.4版.北京:国防工业出版社，1997.

［8］Yeargan J R，Taylor H L.The Poole-Frenkel effect with compensation present［J］.J Appl Phys，1968，39(12):5600－5604.

［9］Gautier J，Guegan G，Guerin M，et al.Operation of short-channel depletion-mode MOSdevices at liquid-nitrogen temperature［J］.IEEE Trans Electron Devices，1991，38(8):1832－1839.

［10］尚也淳，张义门，张玉明.杂质不完全离化对SiC MOSFET的影响［J］.半导体学报，2001，22(7):888－891.