基于虚拟网格的无线传感器网络数据融合算法

甄志军，鲁士文

(中国科学院研究生院，北京100049)

0 引言

无线传感器网络是当前信息科学的热点研究领域，在环境监测、安全监控、科研实验等方面应用广泛［1］。数量众多的传感器节点产生大量的数据，而无线传感器网络的能量供给、存储能力和通信带宽等资源相对有限，不适合传送大数据量。为了减少传输的数据量，一般需要在网络内部对原始采集的数据进行适当的融合和压缩处理。目前已有较多利用时间和空间相关性来进行数据融合和压缩的算法和研究。DIDAS方案［2］是在各一跳节点来对二跳节点采集的数据进行一维离散余弦变换(discrete cosine transform，DCT)来去除数据间的空间冗余度，一跳节点再将压缩后的数据传输至簇头节点。然而，该方案没有考虑时间冗余度，并且仅仅利用属于相同一跳节点分支的各二跳节点之间的一维空间冗余度，而没有将其应用于簇内所有节点之间。基于环模型的分布式时空小波数据压缩算法［3］基于虚拟网格构建环模型，将传感器网络中的数据抽象为一个矩阵，将时间相关性与空间相关性分别映射为该矩阵的小波列变换与行变换，从而利用二维小波变换来去除时间和空间冗余度。然而，虽然小波变换压缩性能较好，但该算法将二维网格区域内的节点构建为一维的环模型，数据之间的二维空间相关性难以充分得到利用。

针对该问题，本文提出一种基于虚拟网格和DCT变换的数据融合算法(virtual-grid and DCT based data aggregation，VDDA)，该算法基于虚拟网格来构建采集数据矩阵，并分别利用时域差分与二维DCT变换来去除时间和空间冗余，从而降低节点能耗和提高网络使用寿命。

1 基于虚拟网格的数据融合算法

本文提出的基于二维DCT变换的数据融合算法VDDA通过将节点分布不均匀的传感器簇划分为多个虚拟网格来去除部分密集节点间的冗余，并便于将其采集的数据组织为二维数据矩阵，连续2个时间点的数据矩阵进行差分以去除时间上的冗余，对该矩阵进行DCT变换和非均匀量化以去除空间上的冗余，最后进行编码以去除码间的冗余，其主要步骤如图1所示。

图1 VDDA算法的处理步骤Fig 1 Processing steps of VDDA algorithm

1.1 传感器簇C划分为虚拟网格G mn

为了有效地进行数据处理，研究中常将传感器网络分为多个簇(cluster)，并假定簇内节点间可以直接通信。每个簇选举一个节点作为簇头节点(cluster head)，簇头节点收集簇内各成员节点采集到的数据。然而，由于传感器网络部署的随机性(如飞机随机投放)等原因，簇内的各成员节点分布并不均匀，某些区域的节点分布密度可能较大，因而存在着一定的冗余节点。如果不作去冗余处理，这些节点将因侦听、发射和接收等处理而给网络带来额外的能量消耗。为此，将包含传感器簇C的矩形区域G划分为M×N个小区域Gmn，每个小区域称为一个虚拟网格(virtual grid)。Gmn表示区域G中第m行第n列个虚拟网格，其中，m∈［9，M］，n∈［0，N］。行列数M，N 的取值由簇的大小、节点相关程度等因素决定，以保证每个网格中平均包含2～4个传感器节点比较合适。在保证可覆盖探测区域的前提下，设定每个虚拟网格内同时工作的节点数量为1，该节点称为工作节点，其他节点处于休眠状态。虚拟网格中某个休眠节点将在合适的时刻被唤醒，以代替因能量耗尽或其他原因而失效的工作节点，以保证整个网络正常工作，达到延长网络生存时间的目的［4］。

1.2 构建采集数据矩阵D

设虚拟网格Gmn中包含fmn个传感器节点，其中的工作节点在某一特定的时间点采集的数据为Dmn，则Dmn即作为虚拟网格Gmn的采集数据，其由工作节点传送至传感器簇的簇头节点H。如果某个虚拟网格Gmn中不包含有任何传感器节点，即fmn=0，则可以根据其邻域多个虚拟网格的采集数据来估计该虚拟网格的采集数据值Dmn，比如选取左右2个相邻的虚拟网格的采集数据的算术平均值。

由此，在某一特定的时间点M×N个虚拟网格所采集的数据在簇头节点H中构成一个M×N的二维采集数据矩阵D

1.3 构建待变换数据矩阵X(i)

簇头节点H构建某一时间点的采集数据矩阵D，并进行后续的数据压缩处理。设D(i)表示第i个时间点的采集数据矩阵，则虚拟网格在第i个时间点与第i－1个时间点的采集数据矩阵差值构成时域差分矩阵

由于时间间隔较短的前后2个时间点采集的数据具有较高的相关性，构建差分矩阵可以有效地去除时间方面的冗余。因此，为了提高压缩效率，对于首个时间点，可对其原始采集数据进行压缩处理，而对其他各时间点，则对差分矩阵来进行相应的压缩处理。然而，如果长时间持续对差分数据进行编码，则容易导致解码端的误码扩散现象。为了均衡解码失真和压缩效率之间的矛盾，可以周期性地在某些时间点对原始采集数据来进行压缩编码，其余时间点则对其差分数据进行压缩编码。设待变换数据矩阵表示为X(i)，则

其中，T表示时间点周期，n为自然数。

1.4 DCT 变换

DCT拥有良好的解相关性能，常用于数据压缩［5］。簇头节点H对待变换数据矩阵X(i)进行二维DCT变换，得到正交变换后的数据矩阵Y(i)

其中，算子F［X］表示对输入矩阵X进行二维DCT变换。由于DCT变换属于正交变换，其能量集中特性使得包含较多能量的低频分量集中至矩阵的左上角区域，而能量较低的高频分量则集中至右下角，该性能有利于后续的非均匀量化。

1.5 量化和编码

对DCT变换后的矩阵进行非均匀量化的各个量化门限即构成量化表，可以通过选择不同的判决门限来调整数据的压缩率。低频分量可选择较低的量化门限以减少数据失真，高频分量则选择较高的量化门限以提高压缩效率。由于待变换矩阵X(i)中差分矩阵数值远小于原始数据矩阵，可以选择不同的量化表来对该2种矩阵分别量化。设Z(i)表示选取量化表QB对变换后矩阵Y(i)量化后得到的数据矩阵，即

然后，簇头节点H对数据向量V(i)进行无损变长编码VLC，得到AC部分的压缩码流

DC部分压缩码流S(i)DC和AC部分压缩码流S(i)AC组成总的压缩码流S(i)，即

簇头节点H将该码流传输至远端的服务器。

1.6 服务器的数据处理

服务器接收到簇头节点H传输来的压缩码流S(i)后，对其进行相应的解码处理。该处理为本地簇头节点H进行数据融合的逆过程，对压缩码流进行相应的解码、反量化、DCT逆变换等处理，即可得到恢复后的采集数据矩阵

2 算法仿真

为了验证算法的性能，利用Matlab来进行仿真。首先构建仿真数据模型以产生具有时间和空间相关性的模拟采集数据，然后利用VDDA算法对其进行压缩，得到压缩码流，最后仿真服务器来对压缩码流进行解压等逆处理，得到还原后的数据，并根据该些数据来计算数据压缩率和失真等指标以评估算法的压缩性能。

2.1 构建仿真数据模型

在仿真中，在一块8m×8 m大小的区域内按高斯分布随机地撒入150个温度传感器节点，该些节点构成传感器簇C。将该传感器簇C划分为8×8的区域G，即M=N=8，每个虚拟网格Gmn中平均包含大约2～4个传感器节点。

为了模拟温度传感器节点在某一特定时间点(如i=1时)检测到的温度数据，需考虑临近节点采集数据之间的空间相关性。据研究，空间距离为d的2个节点所采集到的数据之间的相关系数f(d)正比于d－a，其中，α为大于0的参数［6］。假设每个节点的采集数据(信源)是独立同分布的高斯随机变量，其数值服从高斯分布N(μ，σ2)，其方差σ2与相关系数f(d)成正比。仿真中设α为2，σ2=d－2。

如图2所示，为了简便地模拟各个节点采集的具有空间相关性的温度数据，在区域G中以中心点为基点均匀选取4个一级参考点，再以各一级参考点为基点分别均匀地选取4个二级参考点。假设区域G的中心点采集到的温度为T0=25℃，各个传感器节点在某一时间点(如i=1时)的模拟数据产生步骤为:

1)根据T0产生各一级参考点的温度数据T1i:T1i～N(T0，1/8)，i∈［1，4］;

2)根据T1i得到各二级参考点的温度数据T2ij:T2ij～N(T1i，1/24)，i，j∈［1，4］;

3)根据T2ij产生各个临近工作节点的温度数据Dmn:Dmn～ N(T2m'n'，1/d2)，其中，T2m'n'表示与虚拟网格 Gmn的工作节点最近的二级参考点的温度，d表示该工作节点与该二级参考点之间的距离。

为了模拟其他时间点(如，i=2～5时)，需产生具有时间相关性的随机数据。假设各节点的温度值D(i)服从高斯分布N(μ，σ2)，其期望μ随时间而线性变化，方差与时间间隔的负二次方成正比，即 μ =D(i－1)+kΔt，σ2=(Δt)－2。仿真中可设 k=1，Δt=2，周期 T=5。

图2 仿真数据的产生过程示意图Fig 2 Schematic diagram of the simulation data’s generating process

2.2 仿真参数的选择

1)DCT变换选择目前较常用的快速算法FDCT，以优化计算速度和资源消耗;

2)量化表QB0，QB1需要根据Y(i)的数值范围和期望数据压缩率来进行选择，即选择各个频率分量的阈值门限。该仿真中，选择JPEG压缩标准中的亮度量化表Q进行适当缩放来构成，即 QB0=Q/Qgain，QB1=Q/(Qgain×100)，其中，Qgain为可变量化缩放系数;

3)对量化后矩阵Z(i)的AC分量进行Zigzag扫描后进行常用的霍夫曼编码。

3 性能分析

3.1 数据压缩率和量化缩放系数之间的关系

通过数据融合过程的数据压缩率Ratio来评估数据融合算法的压缩效率

其中，L表示所有节点采集数据的比特长度之和，Length(S(i))为压缩码流的数据长度。量化缩放系数Qgain可以控制变换后矩阵各个频率分量的量化门限的大小，进而调整数据的压缩率Ratio，如图3所示。当Qgain越大，则量化门限矩阵(量化表)QB0，QB1越小，丢弃的数据量越少，数据压缩率Ratio相应地越小。

图3 Ratio和Qgain之间的关系Fig 3 Relation between Ratio and Qgain

从图3中可以看出:Ratio随着Qgain增加而增加，当Qgain达到20左右时逐渐趋于某个稳定值;由于量化表QB0，QB1的选择较合适，原始数据矩阵和差分矩阵的压缩率相近。

3.2 均方误差和量化缩放系数之间的关系

根据所有节点采集的温度数据Dmn和还原后的数据来计算数据融合过程的均方误差(MSE)，以此来评估该算法的数据失真情况

量化缩放系数Qgain同样可以通过控制变化后矩阵各个频率分量的量化门限的大小来调整数据融合过程的MSE。当Qgain越大，则量化门限矩阵(量化表)QB0，QB1越小，丢弃的数据量越少，还原后的数据则更接近原始采集数据，即其MSE越小，MSE与Qgain的关系如图4。

图4 MSE和Qgain之间的关系Fig 4 Relation between MSE and Qgain

从图4中可以看出:随着Qgain的增大而减小，当Qgain足够大时，MSE趋近于零;由于量化表QB1数值较小，差分矩阵压缩后的MSE接近于零。

3.3 数据压缩率和综合评价指数之间的关系

量化缩放系数Qgain与数据压缩率Ratio正相关，而与MSE负相关。为衡量压缩率和失真度的综合效果，定义一个折衷的综合评价指数S

该指数越小，则表明相应方案的效果越好。由于差分矩阵压缩时(i≠nT+1)的MSE明显较小，其综合评价指数S较小，此节仅针对原始数据矩阵压缩时(i=nT+1)。综合评价系数S和Ratio的关系如图5。

从图5可以看出:提出的VDDA算法的综合评价指数显著小于DIDAS算法，因而其综合压缩性能更好。其原因主要在于:1)实现去冗余处理的相关节点范围更广，包括整个传感器簇内的节点，而不限于属于相同一跳节点的二跳节点;2)采用二维DCT变换以充分利用二维空间的相关性，而不是一维DCT变换;3)量化采用非均匀量化方式，即根据各个频率分量的重要程度不同而选择不同的量化门限，而不是采用同一门限的均匀量化。

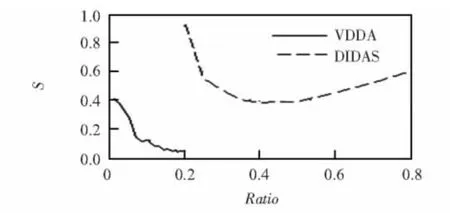
图5 综合评价系数S和Ratio之间的关系Fig 5 Relation between S and Ratio

4 结论

节点数量众多且分布稠密的传感器网络内部产生巨大的数据量，如何有效地对其进行融合和压缩以适应传感器网络资源受限的现状，是传感器网络研究中一项具有挑战性的课题。本文提出的数据融合算法VDDA基于虚拟网格来构建采集数据矩阵，并对该数据矩阵或前后2个时间采集数据的差分矩阵进行二维DCT变换来去除时间和空间冗余度。仿真实验和理论分析表明:该算法具有良好的压缩性能，从而降低网络能耗和提高网络使用寿命。由于小波变换的压缩性能更加优越，利用3D小波变换来去除传感器网络采集数据的时空相关性是今后的研究方向。

［1］Akyildiz I F，Weilian S，Sankarasubramaniam Y，et al.A survey on sensor networks［J］.IEEE Communications Magazine，2002，40:102－114.

［2］曹 萌，陈莘萌.一种基于DCT变换的传感网簇内数据融合方案［J］.计算机工程与应用，2008，44(2):152－154，176.

［3］周四望，林亚平，张建明，等.传感器网中基于环模型的小波数据压缩算法［J］.软件学报，2007，18(3):669－680.

［4］Xu Y，Heidemann J，Estrin D.Geography-informed energy conservation for Ad Hoc routing［C］∥Proc of the Annual Int'l Conf on Mobile Computing and Networking.New York:ACM Press，2001:70－84.

［5］Subhasis Saha.Image compression-from DCT to wavelets:A review［C］∥Spring 2000，2000:12－21.

［6］Apoorva Jindal，Konstantinos Psounis.Modeling spatially-correlated sensor network data［C］∥2004 First Annual IEEE communications Society Conference on Sensor and Ad Hoc Communications and Networks2004，IEEE SECON 2004，2004:162－171.