基于TVAR-HMM 的滚动轴承故障诊断
2010-12-06王国锋李玉波秦旭达李启铭
王国锋,李玉波,秦旭达,喻 秀,李启铭
(天津大学机械工程学院,天津 300072)
机械故障诊断在现代工业生产中起着越来越重要的作用.对反映机械设备状况的振动信号进行信号分析及特征提取,然后利用数学模型进行故障识别是目前故障诊断的主要方法.
滚动轴承是机械设备中故障常发部件,多变的工况条件以及设备自身的非线性,使反映轴承故障的动态信号表现出较强的非平稳特性.目前信号主要的时频分析方法有短时傅里叶变换、Wigner-Ville 分布、小波尺度分析等.这些方法的时频分辨率都要受到不确定性原理的限制,因此无法同时在时域和频域均得到很好的分辨率[1].
故障识别模型以神经网络模型应用最广,但利用神经网络模型进行故障识别需要大量的训练样本,在有限的训练样本情况下,泛化能力差,且优化过程存在陷入局部极值的可能[2];另外,大部分神经网络模型处理的是静态模式分类问题,而旋转机械的故障行为是一个动态变化的过程.
为此,笔者提出了应用时变自回归(time-varying autoregressive ,TVAR) 和 隐 马 尔 科 夫 模 型 (hidden Markov model,HMM)的滚动轴承故障诊断方法.时变自回归模型是一种基于参数模型的时频分析方法.它是在 AR(autoregressive)建模的基础上发展起来的,TVAR 方法得出的时频谱图具有分辨率高、无交叉干扰项以及计算速度快等优点,非常适合处理非平稳信号,已在故障诊断领域有所应用[3-5].隐马尔科夫模型是信号动态时间序列统计模型,能够对一个时间跨度上的信息进行统计建模和分类,具有严谨的数据结构和可靠的计算性能.它能通过较少的样本训练出可靠的模型,并按模式匹配原理,寻找与未知信号最相似的模式作为识别结果,现已成为语音识别的主流技术[6].传统故障诊断方法一直停留在静态分析基础上,忽略了故障变化发展的动态信息,而 HMM 用于故障诊断,可对故障变化的动态信息进行统计分析,能够尽早地发现故障发展的迹象.与神经网络相比,保留了更多训练数据的统计信息,具有更高的识别率和鲁棒性[7].
笔者结合了两种模型的优点,研究了非平稳信号的时变参数建模以及隐马尔科夫建模故障识别过程,并通过实验验证该方法在滚动轴承故障诊断中的可靠性.
1 时变自回归模型
{x(t),t=1,2,…,N }是一非平稳时间序列,TVAR是利用先前值 x (t − i)来估计现在值 x(t),可写成
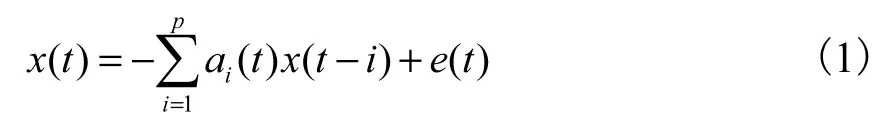
式中:x (t)为信号的采集值;ai(t)(i=1,2,…,p)为时变参数;p 为模型阶数;e(t)为模型残差,服从零均值正态分布.
将时变参数{ai(t),i=1,2,…,p}作为一组基时间函数 gj(t )的线性组合,即

式中:m 为扩展维数;aij为组合的时不变权值.
将式(2)代入式(1),得

式中

这样模型时变参数的估计问题就变成常参数 aij的估计,从而把一个线性非平稳问题转化为一个线性时不变问题.
文献[8]阐述了利用最小二乘法估计模型参数 A的过程,在估计出参数 A 之后就可以根据式(2)计算出时变参数 ai(t)(i =1,2,…,p),继而求解模型方差,即
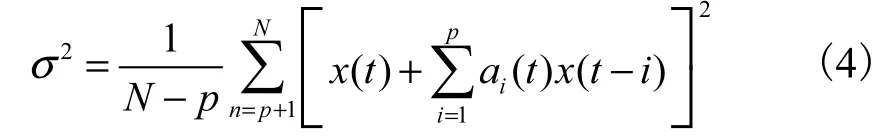
瞬时频率能够通过 TVAR 参数 ai(t )提取.用各个时刻的参数依次计算出每个时刻的参数谱图,叠加在一起就可以构造一个三维时频谱图,因此TVAR 谱函数定义为
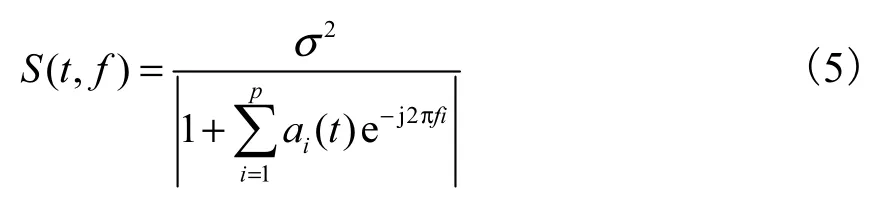
2 隐马尔科夫模型
HMM 是一个双内嵌式随机过程,即 HMM 由两个随机过程组成:一是隐状态转移序列,它对应一个单纯的 Markov 过程;二是与隐状态有关的观测序列.其中隐状态转移序列是不可观测的,只能通过另一个随机过程的输出观测序列进行推断,所以称之为隐马尔科夫模型[9].
HMM 可以记为 λ={Nλ,Mλ,πλ,Aλ,Bλ}或简写为λ={πλ,Aλ,Bλ}.其中 Nλ为模型中 Markov 链的状态数目;Mλ为每个状态对应的可能的观测值数目;πλ为初始概率分布矢量;Aλ为状态转移概率矩阵;Bλ为观测值概率矩阵,对于连续的 HMM,Bλ是一组观测值概率函数.
图1为1 个三状态的离散HMM 的例子,由图可以看出,1 个HMM 可以由1 组状态转移概率以及与每一个状态有关的观测分布概率来定义.
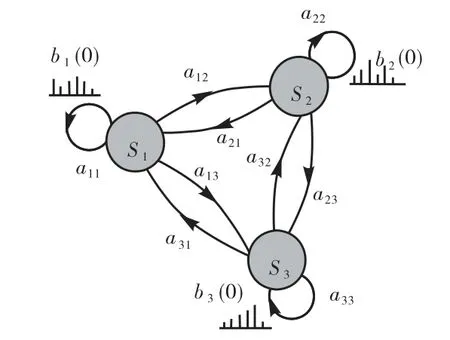
图1 三状态HMM示意Fig.1 Diagram of three-state HMM
一个标准的HMM 模型需要解决概率计算、模型训练和隐状态估计3 个基本问题.
(1)概率计算.给定模型参数 λ={πλ,Aλ,Bλ}、观测序列 O={o1,o2,…,ot},计算观测序列 O 在给定模型下的概率,即计算似然 P(O︱λ)或者对数似然ln,P(O︱λ),它表示参数 λ 拟合数据 O 的准确程度.可通过前向-后向算法对HMM 进行遍历实现.
(2)模型训练,即模型参数估计问题.也就是说,对于初始模型和给定用于训练的观测序列 O={o1,o2,…,ot},如何调整模型 λ={πλ,Aλ,Bλ}的参数,使其能够最好地拟合观测数据 ˆ argmaxλ=f (O⋮)λ,这可以通过EM 算法或Baum-Welch 算法实现.
(3)隐状态估计.给定模型参数 λ={πλ,Aλ,Bλ}和观测序列 O={o1,o2,…,ot},基于某种最优准则估计最可能的隐状态序列 Q={q1,q2,…,qt},即估计产生观测序列的最可能经过路径,这可以通过 Viterbi 算法估计实现.
3 TVAR-HMM故障诊断步骤
图2所示为利用 TVAR-HMM 进行故障诊断的主要步骤.

图2 TVAR-HMM故障诊断流程Fig.2 Flow chart of fault diagnosis based on TVAR-HMM
(1)对不同故障类型的振动信号进行 TVAR 建模,得到时频谱图.建模过程中,需要选定基函数gj(t)、模型阶数 p 和扩展维数m ,文献[10]详细介绍了它们的选择方法.
(2)基于能量法提取故障特征.对信号 TVAR 建模后,故障信息完全体现在时频谱图上.用能量法提取故障特征可以更加有效地提取时频图上的故障信息.文献[11]已研究了这种方法的有效性.其主要过程是:将时频空间划分为若干区域,分别计算其时频局部能量,将时频局部能量作为元素,组成特征向量.
(3)用特征向量训练 HMM 模型.特征向量为HMM 模型的观测序列,故障类型为隐状态,1 种故障类型训练1 个HMM 模型.
(4)利用训练好的模型对测试样本进行识别,即对于未知的观测序列,分别计算在各个模型下的输出概率,然后进行比较,选取输出概率最大的模型,即代表识别出的故障类型.
4 实验研究
为了验证本文方法在实际故障诊断中的应用情况,笔者进行了实验分析.实验在一个故障模拟平台上进行,包括驱动电机、轴承座、扭矩加载器和采集设备,见图 3.通过更换正常轴承和故障轴承进行故障诊断实验.实验测试的轴承是深沟球轴承,型号为6205-2RS,品牌为SKF,其内圈直径为 25,mm,外圈直径为52,mm,滚子直径为7.94,mm.轴承故障用电火花加工而成,故障直径分别为 0.177,8,mm、0.355,6,mm、0.533,4,mm,3 个等级,深度都为 0.279,4,mm.电机转速为 1,797,r/min.振动信号由加速度传感器拾取,分别采集安装无故障轴承、外圈故障轴承、内圈故障轴承、滚子故障轴承时的振动信号,各测得数据 50 组,每组2,048 点,采样频率为12,000,Hz.

图3 实验装置Fig.3 Experimental device
4.1 TVAR建模与特征提取
对无故障、内圈故障、外圈故障、滚子故障4 种状态信号 TVAR 建模时,参照文献[10]中的论述,基函数选择傅里叶函数,采用AIC准则确定模型阶数p.在确定模型阶数前必须先确定扩展维数 m,为了保证信号时频谱的高分辨率和计算速度,一般模型的扩展维数取为 8~12.本次实验选取扩展维数 m=10,依据AIC 准则确定轴承无故障、内圈故障、外圈故障、滚子故障状态下模型阶数 p 分别为 11、15、15、12.
4 种类型的振动信号TVAR 建模后,可以得到相应的时频谱,如图 4(a)~(d)所示.由时频谱中可以看出,不同故障类型轴承的振动信号的频率成分是不同的,并且轴承存在故障时,时频谱中存在时变性与冲击性.图 4(e)为轴承外圈故障信号时域波形,图4(f)为轴承外圈故障信号经傅里叶变换后得到的频谱.通过图4(d)~(f)的比较可以明显看出图4(d)与4(f)中信号的频率成分保持一致,图 4(d)与 4(e)中频率成分发生冲击的时间及时间间隔基本一致.这说明经 TVAR 建模得到的时频谱具有较高的时频分辨率.
基于能量法对时频图进行特征提取时,考虑到速度与精度双重因素,经过多次实验分析,选择将时频谱分为16 部分(过多会影响HMM 训练速度;过少会影响测试的准确度),求每一部分能量的均值,将均值序列归一化作为特征向量.通过特征提取,每种状态得到 50 组 16 维的特征向量,4 种状态共得到 4×50组特征向量.
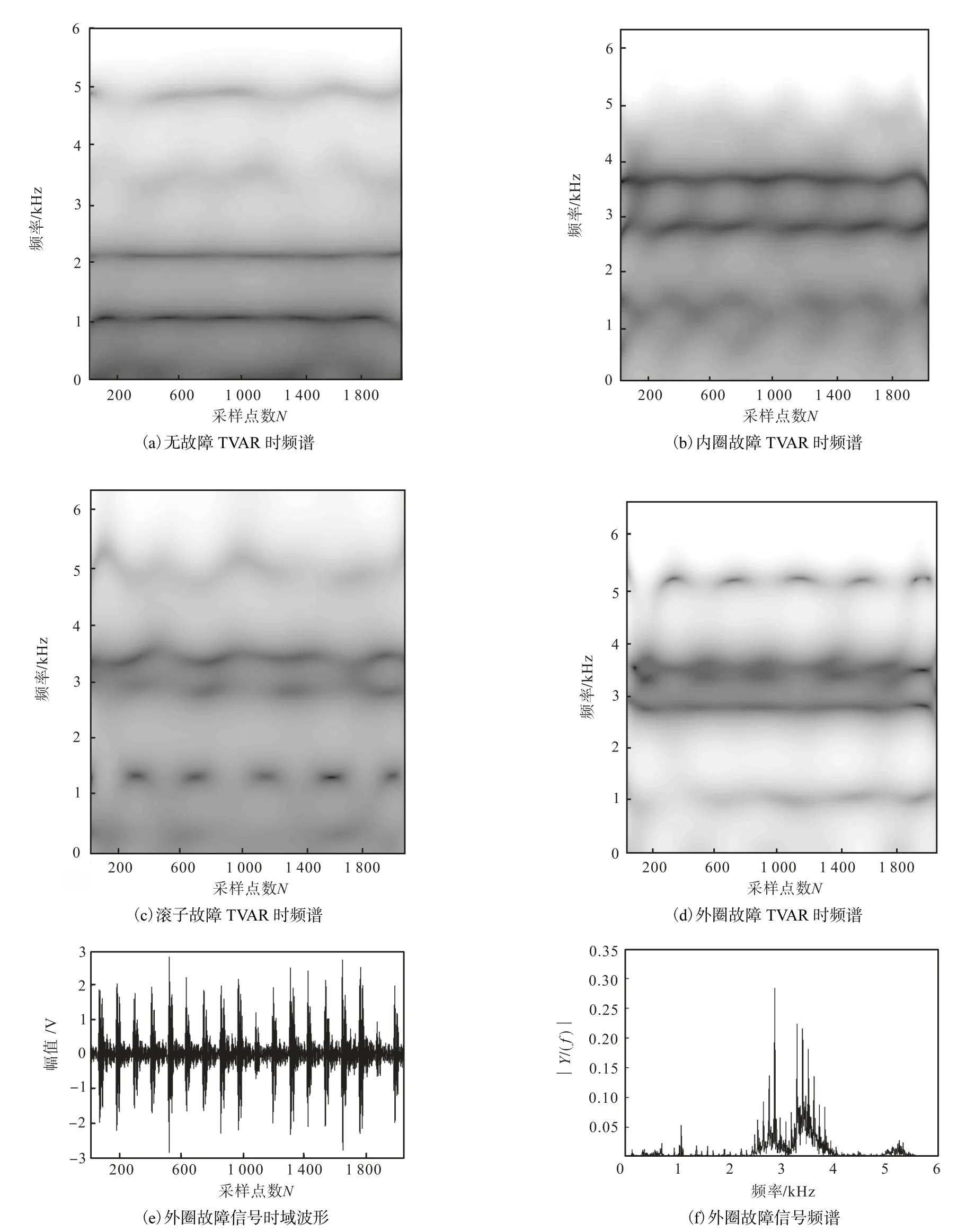
图4 4种状态的时频谱Fig.4 Time-frequency spectra of four states
4.2 HMM建模与故障识别
建模时,采用 4 个隐状态代表无故障轴承、内圈故障轴承、外圈故障轴承和滚子故障轴承,分别记作λ1、λ2、λ3、λ4.模型的观测序列是 TVAR 建模后得到的 16 维特征向量.初始概率分布矢量、初始状态转移概率矩阵和初始观测值概率矩阵均由 Matlab 中rand 函数随机取得,然后归一化.
选用120 组特征向量(每种状态30 组)作为训练样本,训练前需使用Lloyd 算法对特征向量进行标量量化.训练算法为Baum-Welch 算法. HMM 的训练过程中,随着迭代次数的增加,最大对数似然估计值也在不断增加,直到达到收敛误差为止.训练结束后,得到4 个隐状态对应的4 个HMM 识别模型.图5 给出了4 种状态的HMM 训练曲线,所有状态在迭代次数20 都达到了收敛,收敛速度快.
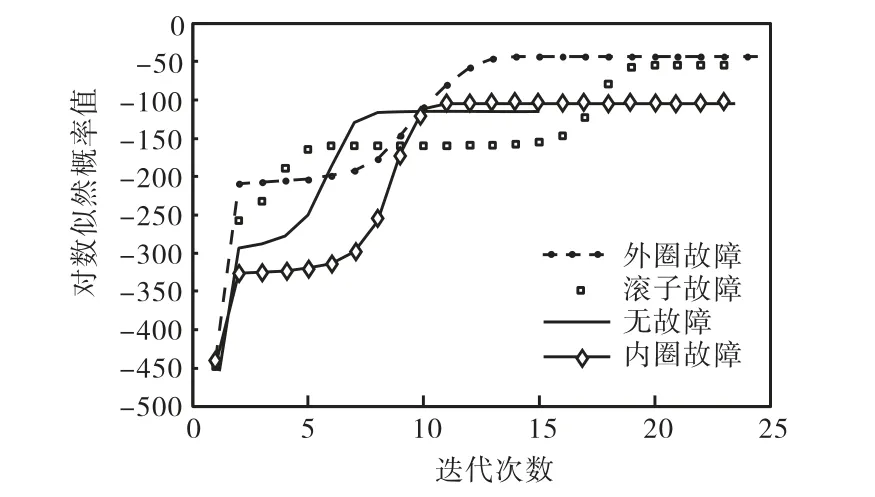
图5 HMM训练曲线Fig.5 HMM training curves
在训练好各状态 HMM 以后,将剩余的 80 组特征向量(每种状态20 组)作为测试样本输入到各状态HMM 模型中(测试前需使用 Lloyd 算法对特征向量进行标量量化编码),在各个模型下能够各自输出 1个对数似然概率值.对数似然概率值反映了特征向量与各 HMM 的相似程度,对数似然概率值越大,特征向量越接近该状态 HMM,特征向量属于使输出对数似然概率值最大的模型所对应的故障类型.识别算法选用 Viterbi 算法.表 1 给出了部分测试样本的测试结果,通过得到的对数似然概率值,可以准确识别出轴承的故障类型;对于同一种故障类型,故障程度越高,得到的对数似然概率值越大.
为了比较基于HMM 和基于BP 网络、RBF 网络故障诊断模型的识别效果,将本实验的数据分别用BP 网络、RBF 网络故障诊断模型来识别.网络的层数设置为3 层,输入层神经元个数为16 个,输出层神经元个数为 4 个.采用与基于 HMM 故障诊断模型同样的训练数据和测试数据分别训练和测试 BP 网络和RBF 网络,得出诊断结果.
图6为本次实验中 3 种模型的故障识别正确率比较.由图6 可见,基于 HMM 故障诊断模型的有效识别率明显好于基于 BP 网络或 RBF 网络故障诊断模型.实验结果表明,基于 HMM 故障诊断模型可以成功地诊断旋转机械的轴承故障,识别率较高,稳定性好.

表1 部分测试结果Tab.1 Some testing results
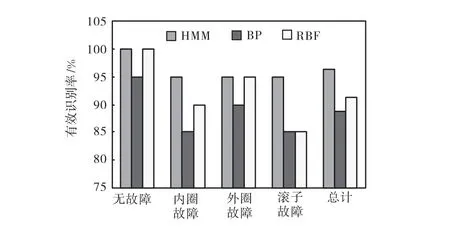
图6 HMM、BP、RBF识别有效性比较Fig.6 Diagnosis accuracies of HMM、BP、RBF
5 结 论
(1)TVAR 模型非常适合非平稳信号的处理,时变参数体现了信号频率的时变性和冲击性.TVAR 建模分析得到的信号时频谱的分辨率高,且无交叉项的干扰,计算速度快.
(2)HMM 模型可以成功地对旋转机械的轴承故障进行诊断,识别率高.由于其为动态时间序列统计模型,非常适合识别信息量大、非平稳性强、特征重复再现性不佳的故障信号,在旋转机械故障诊断中有很好的应用前景.
[1]李 强. 非平稳信号特征提取新方法和实用诊断技术的研究[D]. 天津:天津大学机械工程学院,2003.Li Qiang. Research on New Method of Non-Stationary Signal Feature Extraction and Practical Diagnostic Techniques[D]. Tianjin:School of Mechanical Engineering,Tianjin University,2003(in Chinese).
[2]王奉涛. 非平稳信号故障特征提取与智能诊断方法的研究与应用[D]. 大连:大连理工大学机械工程学院,2003.Wang Fengtao. Research on Non-Stationary Signal Feature Extraction and Intelligent Diagnostic Method[D].Dalian:School of Mechanical Engineering,Dalian University of Technology,2003(in Chinese).
[3]陈 慧,张 龙,李 嶷. 基于 TVAR 的非平稳工况转子故障诊断技术研究[J]. 华东交通大学学报,2006,23(5):116-118.Chen Hui,Zhang Long,Li Yi. TVAR based fault diagnosis for rotation machine under non-stationary condition[J]. Journal of East China Jiaotong University,2006,23(5):116-118(in Chinese).
[4]Wang Guofeng,Luo Zhigao. Fault identification and classification of rolling element bearing based on timevarying autoregressive spectrum [J]. Mechanical Systems and Signal Progressing,2008,22(4):934-947.
[5]张 龙,熊国良,柳和生,等. 基于时变自回归模型与支持向量机的旋转机械故障诊断方法[J]. 中国电机工程学报,2007,27(9):99-103.Zhang Long,Xiong Guoliang,Liu Hesheng,et al. TVAR and SVM based fault diagnosis method for rotation machine [J]. Proceedings of the CSEE,2007,27(9):99-103(in Chinese).
[6]Abramovich Y I,Spencer N K,Turley M D E. Timevarying autoregressive(TVAR)models for multiple radar observations [J]. IEEE Transactions on Signal Processing,2007,55(4):1298-1311.
[7]Tai A H,Ching Wai-Ki,Chan L Y. Detection of machine failure:Hidden Markov model approach[J]. Computers& Industrial Engineering,2009,57(2):608-619.
[8]Hall M G,Oppenheim A V,Willsky A S. Time varying parametric modeling of speech [J]. Signal Processing,1983,5(3):267-285.
[9]Ocak H,Loparo K A. A new bearing fault detection and diagnosis scheme based on hidden Markov modeling of vibration signals [C]//IEEE International Conference on Acoustics,Speech,and Signal Processing. Salt Lake City,USA,2001,5:3141-3144.
[10]Zhan Y M,Jardine A K S. Adaptive autoregressive modeling of non-stationary vibration signals under distinct gear states(Part 1):Modeling [J]. Journal of Sound and Vibration,2005,286:429-450.
[11]刘 伟. 基于能量的时频特征提取研究[J]. 红外与激光工程,2004,33(3):296-299.Liu Wei. Research on the time-frequency feature extraction based on energy[J]. Infrared and Laser Project,2004,33(3):296-299(in Chinese).
