基于轨迹灵敏度的暂态稳定预防控制方法

孙 闻，房大中，袁世强，薛振宇

(天津大学电力系统仿真控制教育部重点实验室，天津 300072)

随着电力市场化改革的不断深入，为了追求更大的经济效益，市场参与者可能将系统运行点推向稳定边界；此外，电网规模的不断扩大以及负荷的加重，也使得电力系统运行的安全问题变得更加突出．近年来，世界各地不断出现大规模停电事故[1-2]，造成了难以估计的损失，如何保证电力系统的安全、稳定和经济运行是重大而迫切需要解决的问题[3]．

电力系统可能发生各种对正常运行造成危害的故障或扰动，为提高系统的稳定性，应采取必要的预防控制措施．预防控制是在危及电力系统安全稳定的扰动发生之前采取的措施，其目的是消除系统运行风险，具体措施包括改变电网结构、调整发电机有功输出等．在传统的垂直管理模式下，预防控制措施由调度中心制定，其主要目的是确保系统的安全运行．而在电力市场环境下，预防控制措施不但要考虑技术的可行性，还应兼顾市场参与者的经济利益．因此，预防控制问题变为在确保系统安全性的前提下实现经济性最优的优化问题．文献[4-5]提出了结合能量函数方法的动态安全调度算法．文献[6]假设故障持续时间内系统各发电机保持相同转速，通过调节发电机的有功输出提高系统的暂态稳定性．文献[7-9]利用灵敏度方法计算发电机有功输出的调整量．文献[10-11]引入最优控制原理用于计算暂态稳定性能指标对控制量的梯度．文献[12]报道的是与紧急控制结合的综合控制方法．

调整发电机的有功输出在技术上可行性较强，通常作为预防控制的主要措施，其难点在于确定调整量．针对这一问题，笔者首先引入电力系统角半径的概念，在此基础上定义了暂态稳定性能指标，通过轨迹灵敏度仿真计算可得到性能指标对发电机有功出力的梯度，该梯度信息可用于指导发电机有功输出的调整．而且，笔者提出了以调整成本最小为目标的最优控制方法，并通过在 10 机典型新英格兰电力系统上的算例验证了新算法的有效性和合理性．

1 暂态稳定控制目标

1.1 电力系统角半径

对包含n 台发电机的电力系统，定义δi和θi=δi−δCOI为第i 台发电机转子相对于系统同步转速和系统惯性中心(COI)的角度，其中是系统惯性中心的角度，Mi为第i 台发电机的惯性时间常数．发电机相对系统惯性中心的功角构成一个以惯性中心为坐标原点的 n 维θ-角度空间．电力系统动态中，系统状态轨迹可映射为各发电机功角对应的相点 (θ1,θ2,… ,θn) 在该 n 维空间中的运动轨迹．令

式中 D 为电力系统角半径，相当于 n 维空间中相点与原点(惯性中心)的距离．在数学上，系统角半径是某时刻所有发电机相对惯性中心的功角iθ的欧几里得范数，可用于衡量发电机功角相对惯性中心的摆开程度．

若系统中一台或多台发电机失去同步，则至少有一台发电机的功角满足由式(1)可知此时

求D 对时间的一阶导数和二阶导数可得D 随时间变化的速度v 和加速度a，即

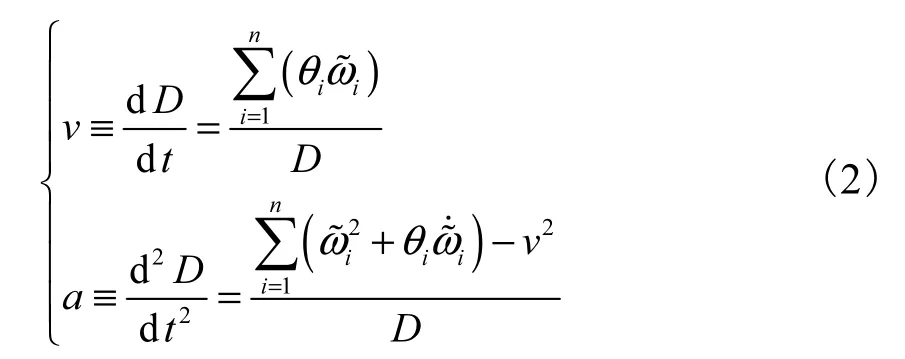
图1和图 2 分别是稳定和失稳情况下 D、v、a 随时间的变化曲线，对应的故障为新英格兰典型电力系统[13]的 28—29 线路的 28 号母线 0 时刻发生三相短路，分别在0.06 s 和0.08 s 后切除故障线路．

图1 稳定情况下D、v、a 随时间的变化曲线Fig.1 Variation of D、v and a with time for the stable case

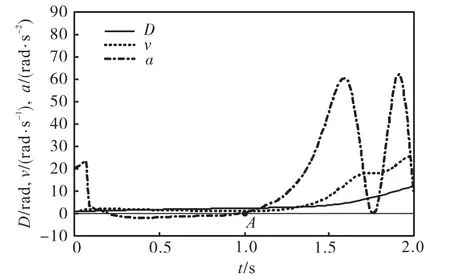
图2 失稳情况下D、v、a 随时间的变化曲线Fig.2 Variation of D、v and a with time for the unstable case

1.2 稳定控制性能指标

由第 1.1 节分析可知，若系统遭受大扰动后是稳定的，角半径 D 将在某一固定的范围内变化，否则将趋于无穷．对有危害故障，需要采取相应的预防控制措施消除安全风险．首先定义暂态稳定性能指标为

式中：Dmax是研究时段内系统角半径的最大值；ρ是阈值．

由式(3)的定义可知，若ρ的取值恰当，J＜0 说明D 是有界的，此时系统能够保持稳定运行，因此 J＜0可作为对有危害故障进行预防控制的目标．下面讨论ρ的取值问题．

如图 1 和图 2 所示，故障切除后，D 随时间变化总要经过一个减速的过程(a＜0)，稳定情况下速度 v经过减速过程后变为负值，此后在正值和负值之间交替变化，因此 D 始终保持在一定的范围内；失稳情况下速度 v 减至某一极小值(如图中点 A 所示，此时v ＞0，a =0)后转为加速运动，此后 v 恒为正，D 单调递增，趋于无穷．上述特性在对华北电网、南方电网等实际电力系统的仿真分析中也得到了充分验证．

为了更直观地说明系统的稳定性问题，分别以 D和v 为横坐标和纵坐标，可得到系统遭受大扰动后的相图，图 3 和图 4 分别是与图 1 和图 2 对应的相图．如图所示，稳定情况下相点总是在某一固定的区域(安全区域)内运动；对失稳情况，相点的轨迹经过点 A 后速度 v 迅速增加，冲出稳定区域，系统失去稳定．在数学上，点A 对应失稳情况下的连续曲线D(t)沿时间轴变化过程中的第 1 个由凸函数变为凹函数(即 a 由负变正)且满足 v ＞0 的拐点．

将点 A 对应的角半径 Dflex作为阈值ρ，则预防控制的目标可写作

结合图 4，式(4)可理解为通过采取适当的预防控制措施，使相点的轨迹始终保持在图中虚线以左的区域内运动．

图3 稳定情况下的相图Fig.3 Phase diagram D -v for the stable case

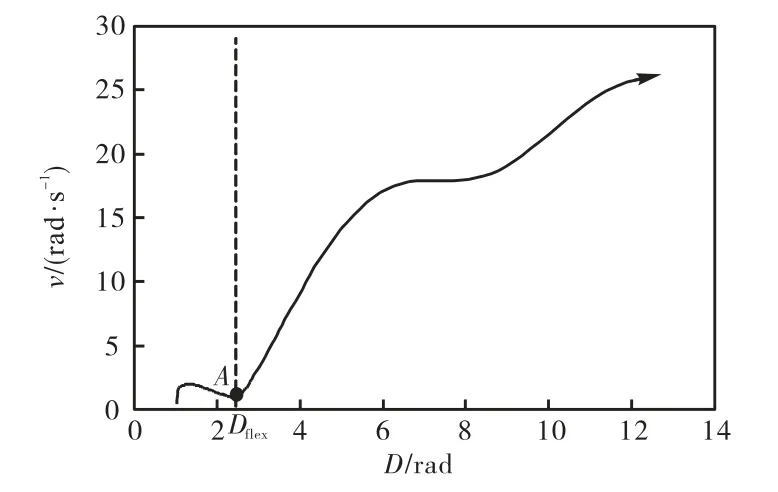
图4 失稳情况下的相图Fig.4 Phase diagram D -v for the unstable case

2 轨迹灵敏度计算

轨迹灵敏度分析是针对微分方程模型研究状态变量变化对参数依赖性的方法，对稳定控制以及参数调整有重要的指导意义．

电力系统的动态行为可用微分代数方程组来描述，即

式中：x 和 y 分别为系统状态变量和代数变量；x0和y0为其对应的初值；α 为可控参数．

式(5)的解记作 x(α,t) 和 y(α,t) ，将其按泰勒级数展开并忽略高阶项，可得

式中 xα(t)和 yα(t)分别为 x 和 y 对α 的灵敏度，称作轨迹灵敏度，反映了系统轨迹与可控参数增量的关系．

将式(5)对α 求偏导数可得

xα(t)的初值[14]为

式(8)～式(10)构成了电力系统轨迹灵敏度的数学模型，是系统(5)的伴随系统．若系统仿真采用隐式梯形积分法，则只需在每一仿真时步增加1 次线性方程求解的工作即可得到轨迹灵敏度系统(8)～(10)的解．

令式(1)对α求偏导数可得到系统角半径 D 对可控参数的灵敏度，即

其中

暂态稳定性能指标J 对可控参数α 的梯度为

将式(11)的结果代入式(13)即可得到 J 对控制量的梯度．笔者以发电机有功出力向量 PG作为控制量，则式(4)可转化为

3 预防控制策略

3.1 数学模型

本文研究的预防控制是通过调整发电机有功输出以消除系统安全运行的潜在威胁．文中以调整成本最低作为目标函数，即

式中：PGi为第 i 台发电机当前的有功输出；PGi,min和PGi,max分别为第i 台发电机的有功输出上限和下限．

3.2 计算流程

式(16)描述的最优控制问题是一般的非线性规划问题，笔者利用 MATLAB 自带的优化软件包对其进行求解．预防控制计算的流程如图 6 所示．图中flag 是标识符，用于记录系统是否稳定，0 表示稳定，1表示失稳；暂态稳定判据为研究时间内发电机转子相对惯性中心的角度均小于指定的门槛值；β 是修正因子，β∈ ( 0,1)；ε是允许的调整误差．

需要指出的是，由于电力系统运行的复杂性，预防控制问题的全局最优解往往无法获得．本文算法的特点是利用性能指标对发电机有功输出的梯度确定发电机有功出力调整的大小和方向，并与迭代计算相结合，最终得到接近全局最优解的控制方案．

式中：Δ PGi是发电机 i 的有功调整量；C ( Δ PGi)是调整量为Δ PGi时对应的经济代价(本文中为发电机调整报价)；NG是参与调整的发电机组总数．

在基于联营体交易的实时电力市场中，各电厂的运行机组需要向ISO 提交调整报价曲线，该曲线包括申请增加出力和申请减少出力两部分[15]，如图 5 所示．由于增加有功输出需要增加燃料成本，故通常情况下增加出力的调整报价高于减少出力的调整报价．

图5 实时电力市场发电机组调整出力报价曲线Fig.5 Bids curve of a unit in the spot market

预防控制的数学模型为

图6 预防控制计算流程Fig.6 Flow chart of preventive control

4 算例分析

算例采用的10 机新英格兰典型电力系统[13]如图7 所示，其中 1 号发电机作为平衡机，系统中所有发电机采用经典模型，负荷采用恒阻抗模型，仿真时间为4 s，暂态稳定功角门槛值为π rad，发电机有功输出调整收敛精度ε=0.1 MW，修正因子β=0.4．为简化计算，假设发电机增加出力和减少出力的报价相等．各发电机的初始有功输出及上下限和调整报价如表 1 所示．算例的计算在 MATLAB 环境下实现，暂态过程的数值仿真采用隐式梯形法．

图7 新英格兰典型电力系统Fig.7 New England 10-generator 39-bus power system

表1 发电机数据和调整报价Tab.1 Generator data and adjusting bid

对两个有危害故障进行了分析，结果如表 2 所示．表中第 1 列是故障线路，28*—29 表示线路 28—29 的 28 号母线侧发生三相短路故障，通过切除该线路消除故障；第3 列和第4 列分别是调整发电机出力前后的临界切除时间(CCT)，可见本文的预防控制算法能够有效地消除稳定性风险．

表2 调整前后有危害故障分析结果Tab.2 Analysis results of severe contingencies before and after generation reschedulings

计算中引入修正因子β是为了防止过量调整，同时提高收敛速度．表 3 给出了β取值对计算结果的影响：β太小，虽然迭代次数减少，但计算精度下降；β太大则会降低收敛性．β的取值在 0.4～0.6 能够兼顾收敛速度和计算精度．

表3 不同修正因子下的计算结果Tab.3 Computation results for different β

本文算例中只考虑了单个故障的情况，若需同时处理多个有危害故障，只需增加约束条件(14)，即增加优化问题(16)中的不等式约束即可．在计算过程中，可能出现可行域为空的情况(如发电机有功输出约束不能够满足导致无解等)，此时说明仅靠调整发电机出力不能满足暂态稳定性的要求，需要结合其他稳定控制措施，相关内容另做研究．

5 结 语

通过轨迹灵敏度仿真计算，得到稳定性能指标对发电机有功输出的梯度，该梯度信息可用于计算有功出力的调整量，最终得到暂态稳定约束下控制成本最小的预防控制方案．该方法的优点是不受元件模型的限制，稳定性能指标包含了所有发电机的功角信息，适用于多机失稳的情况．此外，梯度计算可附在时域仿真程序中同时进行，只需在仿真计算的基础上增加少量的计算量．

［1］印永华，郭剑波，赵建军，等. 美加“8. 14” 大停电事故初步分析以及应吸取的教训[J]. 电网技术，2003，27(10)：8-11，16.Yin Yonghua，Guo Jianbo，Zhao Jianjun，et al. Preliminary analysis of large scale blackout of interconnected North America power grid on August 14 and lessons to be drawn [J]. Power System Technology，2003，27(10)：8-11，16(in Chinese).

［2］李春艳，孙元章，陈向宜，等. 西欧“11. 4” 大停电事故的初步分析及防止我国大面积停电事故的措施[J]. 电网技术，2006，30(24)：16-21.Li Chunyan，Sun Yuanzhang，Chen Xiangyi，et al. Preliminary analysis of large scale blackout in western Europe power grid on November 4 and measures to prevent large scale blackout in China [J]. Power System Technology，2006，30(24)：16-21(in Chinese).

［3］韩祯祥，曹一家. 电力系统的安全性及防治措施[J].电网技术，2004，28(9)：1-6.Han Zhenxiang，Cao Yijia. Power system security and prevention [J]. Power System Technology，2004，28(9)：1-6(in Chinese).

［4］Fouad A A，Jianzhou T. Stability constrained optimal rescheduling of generation[J]. IEEE Trans on Power Systems，1993，8(1)：105-112.

［5］Shubhanga K N，Kulkarni A M. Stability-constrained generation rescheduling using energy margin sensitivities[J]. IEEE Trans on Power Systems，2004，19(3)：1402-1413.

［6］Ding-Heh Kuo，Bose A. A generation rescheduling method to increase the dynamic security of power systems [J]. IEEE Trans on Power Systems，1995，10(1)：68-76.

［7］Wenping L，Bose A. A coherency based rescheduling method for dynamic security [J]. IEEE Trans on Power Systems，1998，13(3)：810-815.

［8］Nguyen T B，Pai M A. Dynamic security-constrained rescheduling of power systems using trajectory sensitivities [J]. IEEE Trans on Power Systems，2003，18(2)：848-854.

［9］孙景强，房大中，周保荣. 基于轨迹灵敏度的电力系统动态安全预防控制算法研究[J]. 电网技术，2004，28(21)：26-30.Sun Jingqiang，Fang Dazhong，Zhou Baorong. Study on preventive control algorithm for dynamic security of power systems based on trajectory sensitivity method[J]. Power System Technology，2004，28(21)：26-30(in Chinese).

［10］房大中，孙景强. 基于最优控制原理的暂态稳定预防控制模型[J]. 电力系统自动化，2005，20(1)：18-21.Fang Dazhong，Sun Jingqiang. Transient stability preventive control model based on optimal control in power system[J]. Automation of Electric Power Systems，2005，20(1)：18-21(in Chinese).

［11］Fang Dazhong，Yang Xiaodong，Sun Jingqiang，et al. An optimal generation rescheduling approach for transient stability enhancement [J]. IEEE Trans on Power Systems，2007，22(1)：386-393.

［12］刘 辉，余贻鑫. 基于实用动态安全域的电力系统安全性综合控制[J]. 中国电机工程学报，2005，25(20)：31-36.Liu Hui，Yu Yixin. A comprehensive security control method based on practical dynamic security regions of power systems[J]. Proceedings of the CSEE，2005，25(20)：31-36(in Chinese).

［13］Pai M A. Energy Function Analysis for Power System Stability [M]. USA：Kluwer Academic Publisher，1989.

［14］Laufenberg M J，Pai M A. A new approach to dynamic security assessment using trajectory sensitivities [J].IEEE Trans on Power Systems，1998，13(3)：953-958.

［15］郭 磊，房大中. 实时电力市场中暂态稳定约束下的阻塞管理模型研究[J]. 电网技术，2006，30(3)：36-40.Guo Lei，Fang Dazhong. A model for real-time congestion management with transient stability constraints[J]. Power System Technology，2006，30(3)：36-40(in Chinese).