大型港口潜堤越浪后港内波况研究*

刘 针，陈志春

（1.交通部天津水运工程科学研究所工程泥沙交通行业重点实验室，天津300456；2.浙江省交通规划设计研究院水运设计部，杭州310006）

波浪在由深海向岸边传播过程中，由于受地形变化和水工建筑物等因素的影响，将发生浅水变形、折射，复杂地形和结构物的绕射和反射、底摩阻、波浪破碎等一系列复杂现象。随着港口工程建设规模的不断扩大，波浪试验所涉及的工程水域也逐渐加大，对于大面积港口，如天津临港产业区和黄骅港工程水域均超过10 km，防波堤设计为潜堤［1-3］。受实验室场地的限制，采用正态波浪物理模型进行试验，模型的水深和波高都可能太小，试验精度难以保证，若采用变态物理模型试验，由于波浪运动相似关系难以同时得到满足，对于模型折射、绕射和反射的影响都较显著的情形，模型观测现象和测定数据原型换算所产生的实际偏差可能较大。波浪数学模型对潜堤越浪的波浪现象模拟不够精确，所以采用波浪物理模型和数学模型相结合的方式研究天津临港产业区港内波况。

1 技术路线

目前，国内外研究波浪问题的数学模型主要有：基于1972年Berkhoff推导出的缓坡方程数学模型、基于1967年Peregrine推导出的Boussinesq方程数学模型和依据势流理论通过求解Laplace方程所建立的非线性波浪模型。针对Laplace方程所建立的非线性波浪方程，一般都采用边界元或者有限元的方法进行求解。不论是边界元数学模型，还是有限元数学模型，计算都耗费大量机时，故这2种方法只适用于小区域波浪传播以及波浪与物体相互作用的问题。

基于线性波浪理论研究波浪传播变形的基础方程有射线方程、能量输运方程、缓坡方程等。缓坡方程由于能够同时考虑波浪的折射、绕射和反射，而被广泛地应用于实际工程中。其中包括椭圆型缓坡方程、抛物型缓坡方程、双曲型缓坡方程和PCPWAVE缓坡方程。TK-2D［4］的PEM波浪数学模型可以模拟大范围的波浪传播，同时考虑波浪的折射、绕射和底摩阻的影响，但是不考虑防波堤和码头建设后的波浪反射以及波浪的破碎。

Boussinesq方程［5-8］数学模型能够直接描述海浪波动过程水质点运动，可以较好地体现波浪传播过程的非线性特点，计算浅水波效果较好，且在处理反射波时较方便。以Boussinesq方程为基础建立的波浪数学模型可以模拟波浪的折射和底摩擦的影响，以及工程后由于建筑物产生的波浪绕射和反射，还可模拟波浪的破碎，但是在空间步长和时间步长上有较严格的限制，对于大面积港口如天津临港产业区和黄骅港工程，水域均超过10 km，而且防波堤设计为潜堤，波浪越浪有破碎产生，考虑波浪破碎时模型计算量非常大，在实际工程中难以实现。

天津临港产业区位于天津港南部，与临港工业区相邻（图1）。该防波堤为半圆型结构，在高水位时允许越浪，护岸为斜坡堤结构，码头结构型式为高桩梁板结构，码头前沿及港池水深-18.0 m。产业区航道近期按5万t级单向考虑，航道宽度160 m，设计底标高-14.0 m，总长30 km，2015年航道达到10万t级规模，水深15.5 m，宽度390 m，总长36 km，航道边坡按1：5考虑，航道先按照近期规划进行计算。本工程区范围约为14 km×10 km。由于外海风浪对工程影响较大，为了对近期围海造陆工程及将来码头泊位形成掩护条件，拟建设防波堤。通过波浪断面模型试验，测定半圆型结构防波堤断面由于越浪产生的堤后次生波大小及传播情况，分析其对港内泊稳条件的影响，为合理确定防波堤堤顶高程和结构设计提供依据。

数学模型是用数学方程来描述工程物理现象，通过数值计算求解方程得出需要的结果，其优点是不受场地比尺的限制，缺点是对建筑物的结构型式、建筑物的反射和越浪等局部物理现象反映较差。本工程区范围很大，适合采用数学模型，同时结合物理模型来克服其缺点。采用波浪数学模型对全港区的波浪进行模拟，数学模型中有关底摩阻系数、越浪参数以及传播衰减特征，采用断面物理模型的结果进行验证，计算得到全港区的波浪场分布情况。通过断面物理模型试验，测定波浪在潜堤堤前和越堤后的传播规律，采用TK-2D的PEM波浪数学模型和Boussinesq方程数学模型，对比研究波浪传播到港内的波况。

当港域风区长度超过1 km时，同时考虑绕射波与局部风浪的合成，数学模型用规范公式可以计算出港区的风成浪结果，叠加法采用以下公式

图1 工程位置和计算点位置Fig.1 Position of project and calculated points

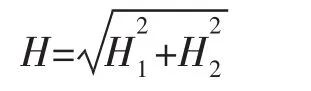
式中：H1为包含越浪影响及口门绕射波的合成波高，m；H2为数学模型码头处风成浪波高，m。

2 试验条件

断面试验在交通部天津水运工程科学研究所波浪水槽中采用不规则波进行。水槽长68 m，宽1 m，高1.5 m。造波机为电机伺服驱动推板吸收式造波机，由生波机械、电伺服控制系统、计算机和无反射模块组成，可以产生规则波与不规则波。模型高程用水准仪控制，用钢尺测量长度，采用电容式波高传感器测量波高，并通过SG-2000型动态水位测量系统对波高进行采集分析。不规则波采用频谱模拟，试验首先考虑采用《海港水文规范》JTJ213-98中推荐的波谱。由于断面试验为波浪正向作用，偏于安全考虑选用波高较大波向的波浪要素（重现期50 a时为 NE（ENE），重现期 2 a时为 E（ESE））。断面波要素和数学模型的边界波波要素见表1。防波堤和码头建成后港区局部风速见表2。

表1 试验用波要素Tab.1 Wave condition

3 试验结果与分析

通过波浪断面物理模型，得到不同堤顶高程、不同水位（水深）、不同波浪正向作用下堤后的次生波波高与入射波的关系。堤顶高程为+5.5 m，设计高水位+4.30 m，重现期50 a波浪作用，堤前H13%波高为4.00 m，波浪越过防波堤，距离防波堤轴线28 m堤根处波高为1.78 m，防波堤堤后次生波沿程波高变化见表3，以堤后堤根处的次生波作为起始波高，对堤后次生波的沿程衰减进行分析。从距离防波堤轴线28 m防波堤堤根处至3 000 m处，堤后次生波的衰减程度为39.9%。对设计高水位堤顶高程+5.5 m，E和ESE向浪作用下重现期50 a港内的波高进行对比。通过调整TK-2D的PEM波浪数学模型中防波堤位置处的高程，调整Boussinesq方程数学模型潜堤位置处网格的孔隙率系数，使波浪越过防波堤后的波高和断面物理模型测定的一致。TK-2D的PEM波浪数学模型的结果见图2，Boussinesq方程数学模型结果见图3。计算点位置见图1，计算点比较见表4。

TK-2D的PEM波浪数学模型和Boussinesq方程波浪数学模型均可通过调整模型参数，模拟潜堤越浪后港内波况，从2个模型的计算结果比较可以看出，在北侧港池主要受绕射波和次生波传播的区域，TK-2D的PEM波浪数学模型结果明显小于Boussinesq方程数学模型结果，在接近口门位置的3#、6#和9#，计算点结果比港池内的计算点波高差别有所减小，主要是由于TK-2D的PEM波浪数学模型绕射不足，也未考虑码头的反射影响。Boussinesq方程数学模型中高桩梁板结构按照20%左右的反射率进行模拟。TK-2D的PEM波浪数学模型的优点是计算范围大、计算速度快，Boussinesq方程数学模型波浪破碎后受空间和时间步长的限制，计算范围不能过大。

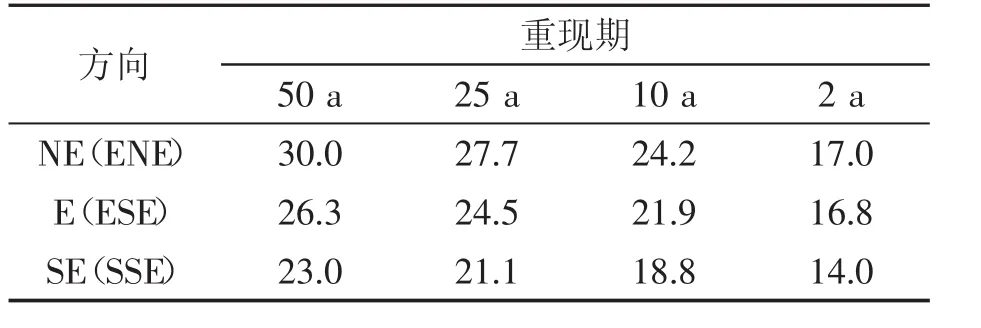
表2 不同重现期风速Tab.2 Wind velocity for different return periods m/s

表3 防波堤堤后次生波沿程波高变化Tab.3 Secondary wave decaying behind breakwater

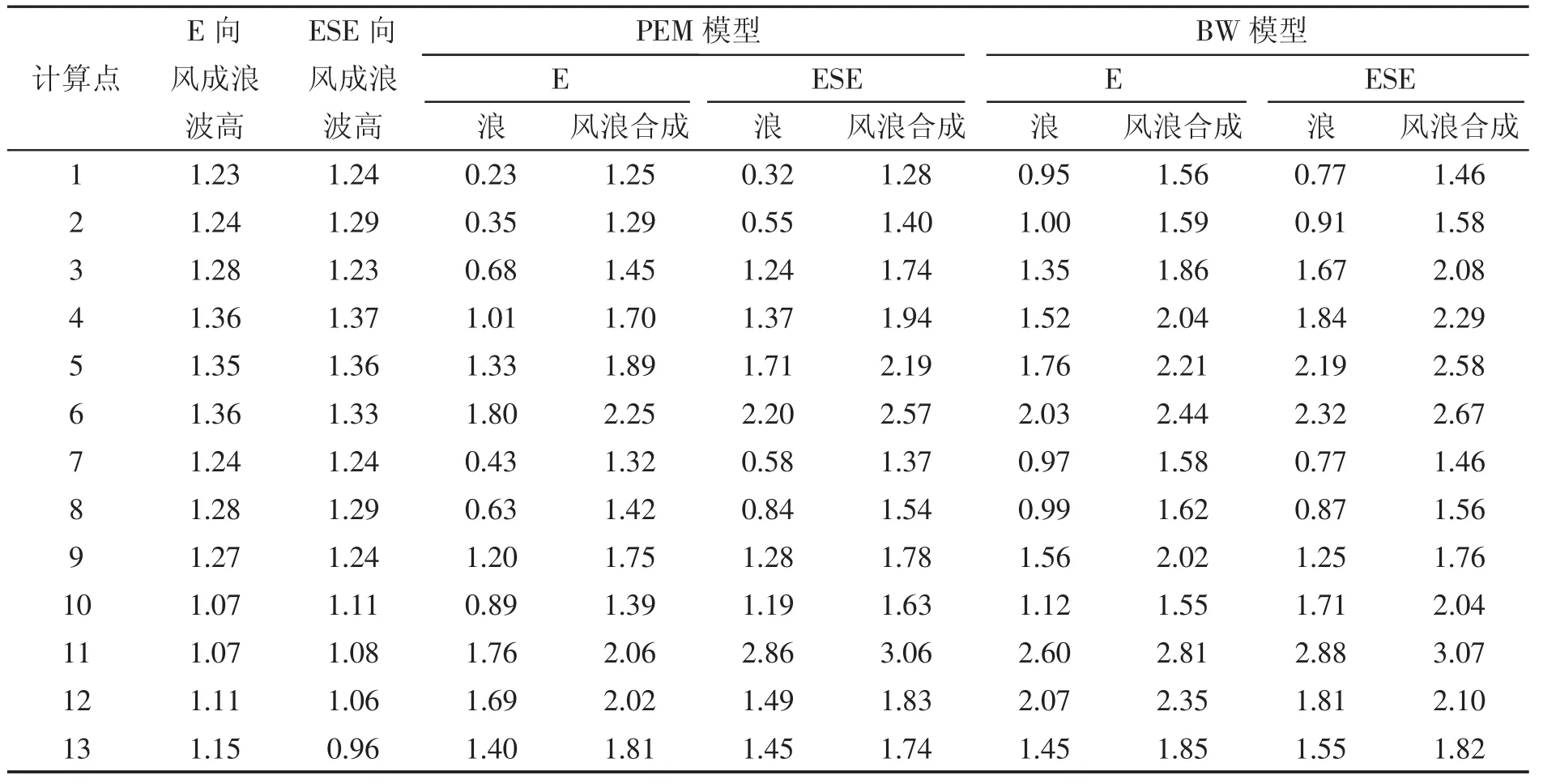
表4 2个模型计算点H13%波高比较Tab.4 Comparison of wave heights from two models m

由于工程区范围比较大，防波堤和码头建成后重现期50 a风速作用下，局部风浪的H13%波高超过了1 m。

4 结论

采用断面物理模型和数学模型相结合的方式，研究潜堤越浪后港内的波况，对TK-2D的PEM波浪数学模型和Boussinesq方程数学模型的研究结果进行对比分析，得到以下结论：

（1）以堤后堤根处的次生波作为起始波高，对堤后次生波的沿程衰减进行分析。从距离防波堤轴线28 m防波堤堤根处至3 000 m处，设计高水位重现期50 a堤顶高程为+5.5 m时，堤后次生波的衰减程度为39.9%。

（2）通过调整潜堤位置处的参数，TK-2D的PEM波浪数学模型和Boussinesq方程数学模型均可以模拟潜堤越浪对港内波高的影响，但是对潜堤越浪后次生波的衰减模拟不够准确，有待于进一步研究。TK-2D的PEM波浪数学模型可以模拟大范围的波浪传播，但是对防波堤和码头建设后波浪的绕射和反射考虑不足，在掩护和反射区，波高较Boussinesq方程数学模型结果小。

（3）由于工程区水域较大，按照规范需要考虑局部风浪的影响，重现期50 a风速作用下，风成浪H13%波高均超过了1 m。局部风浪和从口门传入的波浪叠加后，码头前波高有较大幅度的增大。所以在大水域港口需考虑局部风浪的影响。

［1］张娜，吴海峰，曲淑媛.潜堤及透浪式建筑物的波浪数值模拟研究［J］.中国港湾建设，2009，10（5）：28-31.ZHANG N，WU H F，QU S Y，et al.Wave Numerical Simulation Study on Submerged Jetty and Permeable Works［J］.China Harbour Engineering，2009，10（5）：28-31.

［2］康万军，陈汉宝，唐文帅.潜堤次生波波高规律的研究［J］.水道港口，2009（5）：336-341.KANG W J，CHEN H B，TANG W S.Experimental study on secondary wave height over submerged breakwater［J］.Journal of Waterway and Harbor，2009（5）：336-341.

［3］谢世楞，蔡艳君.半圆型潜堤后的波高分析［J］.港工技术，1999（4）：1-3.XIE S L，CAI Y J.Analysis of Wave Heights behind A Submerged Semi-Circular Breakwater［J］.Harbor Technology，1999（4）：1-3.

［4］李孟国，张华庆，陈汉宝，等.海岸河口多功能数学模型软件包 TK-2D 研究与应用［J］.水道港口，2006，27（1）：51-56.LI M G，ZHANG H Q，CHEN H B，et al.Study on multi-function mathematical model software package TK-2D and its application for coast and estuary［J］.Journal of Waterway and Harbor，2006，27（1）：51-56.

［5］DHI Software.MIKE21 Boussinesq Waves Model User Guide［M］.Danmark：DHI Software，2005.

［6］Boussinesq J.Theory wave and swells propagation in long horizontal rectangular canal and liquid contained in this canal［J］.Journal of Mathematics Pures App quees，1872，17（2）：55-108.

［7］Fuhrman D R，Bingham H B.Numerical solutions of fully non-linear and highly dispersive Boussinesq equation in two horizontal dimensions［J］.International Journal of Numerical Method if Fluids，2004，44：231-255.

［8］Fuhrman D R，Bingham H B，Madsen P A.Nonlinear wave-structure interation with a high-order Boussinesq model［J］.Coastal Engineering，2005，52：655-672.