挟沙水流的能量级串和泥沙输移特性综述*

刘兆存，邓宇忠，王万战，范玮佳

（1.重庆交通大学内河航道整治技术交通行业重点实验室，重庆400016；2.黄河水利科学研究院泥沙研究所，郑州450003）

水沙相互作用机理一直是泥沙运动力学研究的重点，与紊流的研究进展密切相关。起初，人们认为流体的脉动是随机的，20世纪60年代以前水沙作用机理取得的成果都基于这个图像。随着猝发现象的发现和深入研究，20世纪90年代中期，国家自然科学基金委员会将其列为水沙方面优先资助的方向。近年来，随着流体运动中Soliton和Cs-soliton结构的深入研究，通过实验发现流体运动中Soliton和Cs-soliton结构和紊流的输运等一系列性质密切相关，探讨水流结构和水沙机理，并服务于实际工程，是十分有意义的。

流速分布和能量级串是清水水流研究的2个主要领域，两者之间通过拟序结构互相关联。反映到挟沙水流，挟沙能力和水流阻力是理论和工程关心的2个主要方面，是泥沙和水流之间互相耦合作用的结果。本文主要评述含沙水流的能量级串传递过程及其特点，能耗级串与含沙水流流动结构之间的互相关系，挟沙水流流动过程中水流与泥沙之间的耦合作用对水流特性的影响，能量级串与泥沙运动，如泥沙起动、挟沙能力、泥沙浓度分布等之间的关系。从比较清水水流与挟沙水流之间的异同出发进行评述。重点论述推移质泥沙运动的特性，着重从运动学的观点建立推移质泥沙运动的物理图像，侧重于唯象描述。从动力学出发，构造合适的物理模型，描述拟序结构与泥沙运动的定量关系，则另文论述。

本文首先论述了泥沙起动和推移质输移的特点；为了便于比较，简要介绍清水水流与低含沙水流的运动特性，然后论述高含沙水流运动特性的机理；从能量级串和推移质运动的关系入手，分析高含沙水流流动的内在机理；从悬移质、推移质和水流之间互相耦合作用出发，探讨含沙水流的流动机制。

1 推移质运动的特点

沿河床床面滚动、滑动或跳跃前进的泥沙称为推移质。其中滚动和滑动前进的泥沙常与床面接触，因此称为接触质，而以跳跃前进的泥沙称为跃移质。推移质和悬移质运动之间有本质区别，其运动规律、能量来源及对河床的作用有本质不同［1］。支持推移质运动的是颗粒间的离散力，推移质直接消耗水流的能量，而悬移质只与水流的紊动作用相关，不直接消耗水流的能量。在单位时间、单位水体从泥沙中取得的势能为

式中：u为平均流速；S为重量含沙量；γs、γ分别为泥沙和水的比重；J为水力坡降。如果泥沙以速度ω下沉，在含沙量高时，单位时间内需从单位水体的紊动动能中取得的能量为ω，如果 E≥E，即 ω≤uJ，12泥沙为冲泻质，否则为床沙质。冲泻质和床沙质泥沙均可通过推移质或悬移质形式运动。

严格来讲，紊流本身是非恒定的，紊动的产生与发展，流体涡旋的生成与变形皆为非恒定过程。一般认为，非恒定流可分为两大类：第一类为流体运动在外界条件下的响应；第二类为流动本身的不恒定性，即边界条件不变，流动自身所产生的非恒定现象。恒定流一般是对特定流动状态的简化。由于影响床面泥沙颗粒起动随机性的因素众多：（1）作用在沙粒上流速的脉动性；（2）颗粒形状的不规则性；（3）泥沙在床面上的排列及所处位置的偶然性；（4）床沙组成的非均匀性；（5）粗细颗粒泥沙相互混合的不确定性及它们之间相互荫暴作用的瞬变性；（6）细颗粒泥沙粘性作用的复杂性；（7）泥沙补给条件的不稳定性等，使得推移质运动缺少可靠的实测资料。由非均匀沙组成的河床，只要发生冲刷，就会出现粗化现象。随着粗化的进行，一定水流条件下的起动粒径逐渐变小。河床粗化完成时，虽然水流强度大于粗化层下细颗粒的起动条件，但泥沙受到粗化层的保护作用而不能起动。粗化后床沙呈均匀化，大于起动粒径的颗粒数量显著增加，而小于临界颗粒的泥沙显著减小，非恒定非均匀流中，河床变形对流量变化的响应有一定滞后，这种迟滞与床沙组成有关。宽级配的卵石推移质输移具有明显的间歇性、阵发性，其输沙率与水流强度、来沙特性、床沙组成及床面微地貌之间形成复杂的反馈关系。非均匀沙起动规律和推移质输沙特性是推移质输移研究中的2个重要方向。水流的脉动作用使得作用在床面附近的拖曳力呈随机性；又因泥沙颗粒的大小、形状、分选以及泥沙组合的形式不同，使得床面附近泥沙起动的临界拖曳力发生很大变化，至今也未得到公认的且能精确预报输沙率的计算公式。研究推移质输沙主要是探讨推移质输移特性与整个河床中的水流条件、泥沙条件和边界因子等诸多影响因素之间的互相反馈随时间以及空间的变化特性。

推移质和悬移质对流速分布有重要影响。含有推移质水流的平均流速较清水情形下减小（以同条件下的清水水流作为比较的标准，下同），而流速梯度增加；含有悬移质的水流，推移质的存在同样使平均流速减小，主流区的流速梯度有所增大。推移质中绝大部分颗粒以跃移形式运动，且悬移质运动也是由推移质所支撑的。关于颗粒在水流中是如何扬起的观点主要有：（1）床面附近的水流速度梯度使得泥沙颗粒受到一个向上的作用力，即上举力；（2）水流对沙粒的垂向作用力除了上举作用力外，还有水流的脉动上举力；（3）近底水流猝发紊动的拖曳力；（4）局部的水流分离、压强的剧烈脉动以及产生的附加质量力等将床面上的泥沙卷扬起来送到主流区。一般而言，泥沙运动形式可概括为：起动→滚动（间或滑动）→滚动和跃移相间→连续跃移→跃移和悬移相间→悬移。沙粒一般是由跃移转为悬移，沙粒的扬起一般以跃移运动过程为主。近年来一般认为单个泥沙颗粒的单步步长及跃高的概率密度均服从Γ分布，相对步长也具有相同的分布规律，但随着颗粒密度的减小或水流速度的增大，相对步长概率分布的峰值变小，而颗粒粒径的变化对相对步长的概率分布影响不大。

按照钱宁先生的观点，描述推移质运动公式的着眼点虽然各不相同，有用拖曳力，有用平均流速，公式结构也差别很大，但大致可以分为：（1）以大量实验为基础建立起来的公式，以Meyer-peter公式为代表；（2）以概率论和水力学互相结合的方法建立起来的推移质输沙公式，以H.A.Einstein公式为代表；（3）根据普通物理学的概念，通过分析泥沙受力和运动情形建立起来的公式，以R.A.Bagnold公式为代表；（4）结合统计和力学方法，辅助以量纲分析和实测资料校验，这类代表公式包括 F.Engelund，M.S.Yalin，P.Ackers and W.R.White等公式。近来发展起来的众多推移质输沙公式，大致是沿着上述思路展开的，如窦国仁公式等。据钱宁的研究，这些公式虽然形态各异，但可以统一表述为单宽推移质输沙率和水流强度之间的函数关系。令

式中：qb为推移质单宽输沙率，以泥沙干重计；g为重力加速度；d为泥沙粒径；γs、γ分别为泥沙和水的比重。水流强度参数ψ为

式中：τ0为作用在单位床面面积上的水流拖曳力，即床面切应力；h为水深。如果假定床面保持平整且泥沙起动判别标准为φ=0，对应的ψ=0.047的条件下，推移质的输沙公式可以写为φ=f（ψ）的形式。从工程实用的角度考虑（除高、低强度输沙2种极端的情形外），上述众多学者的不同形式的公式均可满足工程的需要，但没有一个公式是普遍适用的。

孙志林［2］的研究表明，推移质泥沙的单步运动距离L和单步运动时间t，可以表示成为水流参数的函数形式

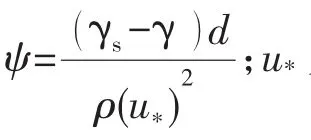
式中：u*c为泥沙起动摩阻流速。在一定条件下，式（5）和实际相符。

得到上述公式的前提均为平均流和泥沙作用是即时的，含沙水流和清水水流流动特性相同。对于非均匀沙的情形，公式中并未考虑单个颗粒起动的特殊物理机制，难以适应各种复杂情形。水流和泥沙的运动图像都是基于恒定、均匀流的结果，可以认为是对经验和试验资料在理论指导下的系统总结，是半经验的唯象理论的结果。从工程实用的角度来看，流速较大时，水流的紊动强度也较大，对于粗糙边界的情形更是如此。但是由于不同的边界情形和上游来流条件对紊动强度有较大的影响，从紊流模化的理论来看，会影响流场内部的脉动动能和能量耗散率的分布，进而影响泥沙的起动和输移。摩阻流速仅仅是从边界阻力的角度反映流速分布形状的一个指标，相同的摩阻流速并不意味相同的流速分布，相同的流速分布并不意味相同的流场结构，对于均匀流情形下也是如此。就目前泥沙运动力学发展的水平而言，从单个颗粒的运动图像出发，应用统计力学或分析力学的知识，进行影响因素全面的综合，得到泥沙与水流相对精确的因果关系——显然反映泥沙和水流运动情形的特征物理量是时间和空间的点的函数，这在目前是不现实的。人们对于非恒定、非均匀输沙的研究才刚刚起步。从物理上考虑，泥沙和水流的作用有滞后性，这种滞后性不仅和水流运动有关，也和泥沙特性有关，和初始、边界条件都有关系。上述公式是近似的半经验的结果。非恒定、非均匀流条件下的非均匀沙的起动和输运特性研究，是一个值得关注的方向。

2 清水水流和低含沙水流的流动特性

窦国仁小组猝发现象［4］的实验表明，在最靠近壁面外，随机排列着相反旋转的纵向涡旋，通常称之为壁面的条纹结构。实测统计表明，条纹结构的纵向（流向）尺度、竖向（垂直流向向上）尺度和横向（x，y，z坐标轴构成右旋坐标系）尺度分别为=100～2 000，=10～25100，其中v为运动粘性系数；在条纹结构上面的近壁层，是经常发生猝发的紊流层。猝发结果导致具有强烈脉动能量的较小尺度涡旋的运动（载能涡旋）。实测资料表明，载能涡旋的尺度大致为（和条纹结构采用相同的无量纲化过程，下同）：=20～4015～20=60～100。载能涡旋存留距离约为边界层厚度的0.5～1.5倍，而瞬时雷诺应力可以达到时均值的60倍；猝发层上面为对数层，时均流速呈对数分布，较小尺度涡旋的运动具有某种典型性。典型含能涡旋的纵向、竖向和横向尺度分别为=200=100100～200，其存留间距约为c+=1 000。窦国仁等认为，Kolmogorov和Batchelor针对各向同性紊流提出的如下3个假定，也适用于其他紊流，如剪切紊流中的局部各向同性区域，具有普遍意义。（1）当雷诺数足够大时，存在一个处于统计平衡状态的大波数区，其特征长度 η 和特征速度u可组合为 η=（υ3/ε ）0.25和u=（ευ）0.25，用该尺度衡量统计平衡区的运动，紊流将保持自身相似性；（2）当雷诺数足够大时，必存在紊动特征值单值地决定于 ε 的惯性区间，满足=（εlα）1/3=（ε/α）1/3，其中为波数为α的漩涡脉动流速均方差，lα为漩涡尺度；（3）在与统计平衡区相邻的较低波数区内，紊动完全取决于ε、υ和t的平衡区，且满足εt2/υ=c，其中c为常数。而ε为粘性耗散率，t为时间。

毛野［5］的实验研究表明，猝发周期与粗糙高度（ks）雷诺数的关系是，当Re*＜1时，猝发周期变化不大；当Re*＞5时，猝发周期增加。随着Re*的增加，猝发呈多头喷发态势，清扫与喷发相持时间延长。喷射范围和清扫范围均有增大趋势，清扫范围是喷射范围的1～2倍。当Re*增加到一定程度时，原较清晰的紊流猝发周期变得较为模糊。观测到的喷射水平距离可达0.038 m，实际清扫的水平距离可达0.047 m。光滑壁面情形下的边界层猝发周期TS（+以边界层的无量纲化，δ是边界层厚度）满足如下关系

式中：Rθ为动量雷诺数。在粗糙壁面的情形时，边界层猝发周期TR+为

在天然河道中，以恒定流流动方向为x的正向，垂直于流动方向向下为y正方向，坐标原点位于水面，x，y，z符合右手螺旋法则。如果取

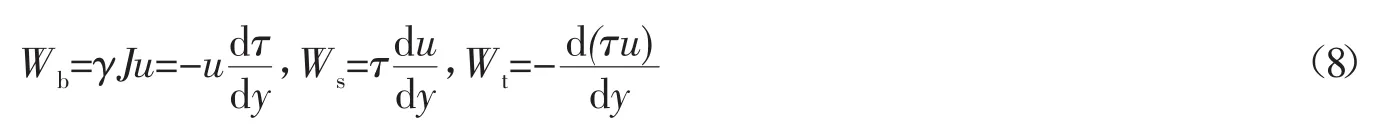
此时的河道水流能量方程为

沿用传统的称谓，Wb为单位水体单位时间所提供的势能，称为提供能；Ws为单位水体单位时间所消耗的能量，称为消耗能；Wt为单位水体单位时间输出和输入的能量差，即通过水体所传递的能量，称为传递能。传递能沿整个水深积分值为零，只表示能量向不同位置和方向的传递特性。以x方向为例，恒定流中

取

则恒定平均流能量方程为（带撇表示脉动量，取Reynold平均）式（9）。从涡动力学可知，边界是涡的发源地，流速场其实是一个涡量场。

从物理上看，能量传递和不同阶段对应的不同结构密切相关，能量耗散和当地激发可能是由共振和锁频造成的，表现为紊流的易感受性。平均流不直接与紊动有关，而是先蜕化为紊动产生能，再影响脉动。这个过程是动态、双向的。对于明渠，Wb、Ws、Wt分布的大致图像是：提供能主要是由水面向水底传递，脉动能主要是由水底向水面传递。河底，尤其是推移质输运的河底，是紊动能的主要发源地。边界层内的能量主要以耗散为主，尾流区能量以提供能为主，相应的含能涡占多数。对数流区的能量，可以处于传递能总量近似为零的近平衡态。具体图像可参考文献［6-8］的结果。

从物理的唯象机制来看，对清水水流而言，无穷层次的流动结构只是流体动能因有效粘性作用从平均流传输到脉动流，再经由涡团级联散裂过程及分子粘性作用最终变为分子热的确定论过程。泥沙的存在只改变能量分配和流动的过程，主要影响紊动产生能。漩涡变形和漩涡之间的相互作用，并不改变能量最终耗散的方向。

窦国仁的泥沙起动研究［9-10］表明，粗颗粒泥沙的粘结力和水柱压力很小，起动后仍然在床面附近运动。细颗粒泥沙的粘结力和水柱压力远超重力，起动后突然失去粘结力和水柱压力而悬浮。对于平整泥沙床面，当泥沙粒径小于0.5 mm，其糙率高度与粒径基本无关，保持为常值；在粒径大于0.5 mm、小于10 mm时，糙率高度约为2倍的中值粒径；当粒径大于10 mm时，糙率高度与粒径的关系呈非线性关系。单位时间、单位底面积上的水体为保持一定的沙量浓度S*不沉而需要的能量为

式中：ρs为泥沙的密度。底沙在水流的作用下被输运时，所消耗的水流的能量为E=efρghJun0d2，如果被输移的泥沙以速度νs跳离床面，单位时间所讨论的范围内有n0颗泥沙在水流作用下被输移，则其所需要的能量为 Ej=n0(ρs-ρ)gd3νs。当单宽输沙量与其输沙能力相等时，单位时间内从床面冲起的底沙量应等于单位时间内沉在床面上的底沙量，即保持动态的平衡。如用n1表示在床面上运动的底沙颗粒数目，则有n0νs=n1ωb，水流作用下的单宽输沙率为

式中：ej，ec为系数。

窦国仁对于泥沙和水流相互作用的思想［11-14］不仅揭示了流体运动过程中的局部水流结构，也反映了拟序结构是由不同的紊流斑块构成的这个事实，虽然流体运动过程中，级串以能量耗散为主，但在局部区域，有可能发生能量逆转，即能量由脉动流转化为平均流。泥沙和水流运动的不同步，在泥沙颗粒后面会引起流体分离现象，挟沙水流对于小尺度漩涡的影响会更大。在紊流衰减的后期，挟沙水流的洛强斯基不变量和清水水流可能不同，相应的含沙水流的能谱关系也必然和清水不同，这方面缺乏定量的研究结果。涡是流体运动的肌腱这个图像不变，这是挟沙水流流动具有自相似性的基础。

泥沙的存在使水流的能量分布更均匀。低含沙水流的推移质运动的物理图像可以近似为，在平均流作用的基础上，（1）叠加一个随机的脉动流场。在不同位置，脉动流场强度不同。对于恒定均匀流，在某一空间点，流场强度可以近似用高斯正态分布描述；（2）叠加一个紊流的拟序结构场，这个场形成的物理基础就是猝发；（3）由于泥沙分布的随机性，还应该叠加一个描述泥沙互相荫蔽的扰动场。总之，泥沙起动是确定因素和随机因素互相作用的结果。在此基础上，单个泥沙的起动条件有一个门限函数，超过这个函数值，泥沙就会起动。对于不同的泥沙，起动的门限函数值不同。研究推移质的运动，就化为对函数值的统计分析。

3 高含沙水流流动机理分析

一般认为，高含沙水流或含沙量达到一定值的流体属于宾汉体。实验表明，二维状态下的本构方程为

式中：τ为切应力；τb为宾汉极限切应力；η为刚性系数，有时也称为粘滞系数；为流速梯度。对于非流核区内的脉动结构，窦国仁［15］得到光滑区时均和脉动流速为

钱宁小组对于宾汉体泥浆紊流［16-18］的研究表明，泥浆紊流的频谱分布异于清水，低频流速脉动能量在清水紊流中为10%～20%，而在泥浆紊流中则可高达40%～50%，泥浆紊流的紊动漩涡主要产生于间歇紊流层与强紊动层之间，在y+=3～10的范围内，其脉动分布和变化规律都与清水水流类似。清水水流中，近底层的平均流速和雷诺应力分布均很不规则，流向、法向和展向的脉动分布不同，但在含沙水流中缺乏精细的对比研究成果。

据窦国仁小组对宾汉体的研究［19］，在浑水中，随着含沙浓度的增加，泥沙颗粒间的距离在不断缩小。当间距缩小到最低值不再缩小后，浑水中的含沙浓度就不再增高，这时候的含沙浓度称为浑水的极限含沙浓度。Sv表示体积含沙浓度，Sv,max表示极限体积含沙浓度，则

相应的重量含沙浓度为

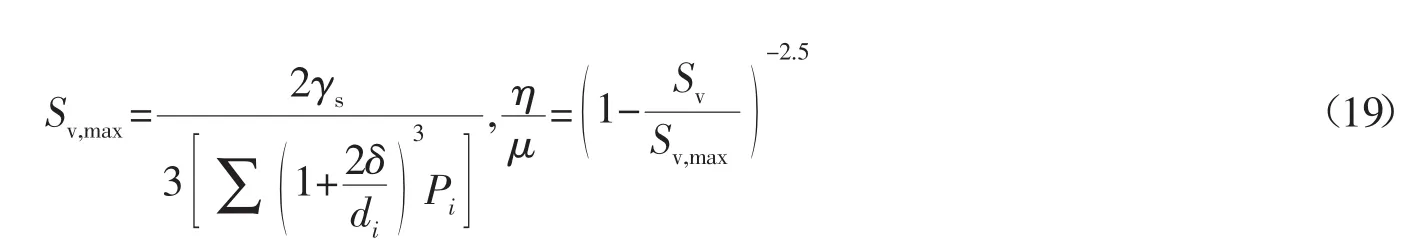
式中：μ为清水的动力粘性系数。天然泥沙时

均匀沙时

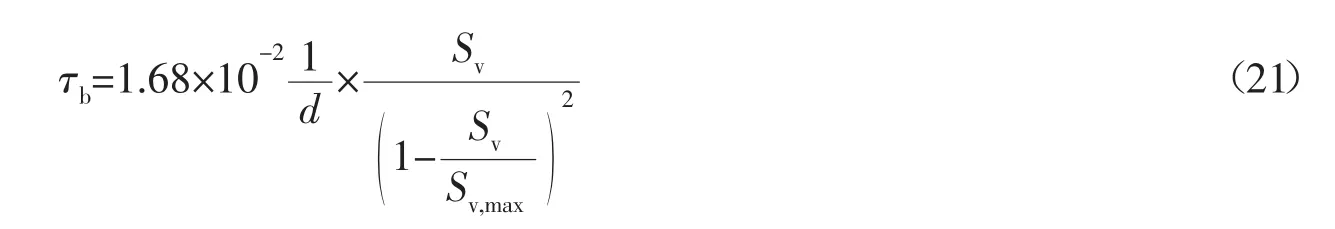
式中：Pi为粒径为di的泥沙所占的百分比。

高含沙水流和清水水流的区别在于一个是牛顿流体，一个是宾汉流体。可以证明，二者的连续性方程相同，流体速度分解的Helmholtz公式相同。区别在于宾汉流体的本构方程不同。动量方程为

式中：fi为单位质量力，有理由相信由于宾汉极限切应力的存在，压强传递的帕斯卡定律不成立。进一步，当i≠j时，切应力之间有σij≠σji，使得宾汉流体和牛顿流体的运动性质不同。由于宾汉极限切应力和刚性系数是含沙量和泥沙性质的函数，可以推断，高含沙水流的能量分布形式、内部能量传递特性和清水水流不同。高含沙水流揭河底现象以及产生浆河时的流动特性是能量级串特殊性的反映。实验表明，在流速较高时，高含沙水流保持了流动的自相似性，形成了对数型的流速分布。但由于本构方程的不同，高含沙水流中漩涡的稳定准则、拟序结构的自相似性、能谱分布特性、平均流和脉动流的能量级串以及漩涡的破裂、重联、合并关系等，和清水水流相比不同。关于这方面的理论与实验结果值得探讨。

4 含沙水流流动的能量级串特点

窦国仁指出，单纯水流的挟沙能力为

式中：c2为系数；h为水深；n为曼宁系数。钱宁根据维利坎诺夫的重力理论，得到

从而有

最终得到实验支持的悬移质泥沙的含沙量分布为现在沿用的形式

主题学习模式的局限性是设计学习活动困难，故不是每位教师都能熟练自如地应用。学习活动设计得好坏直接影响学生的学习效果，无论是学生还是教师，都很难把握所选主题的大小、难易程度、意义价值等，这在一定程度上阻碍了主题学习的推广。

拜格诺认为泥沙在水流中以沉速ω下沉，但悬移质的重心作为一个整体又能保持在一定的高程，这意味着水流必须以ω的速度将泥沙举起。在单位床面面积以上的水体中，水流紊动因泥沙悬浮所做的功为W′ω，其中W′为单位床面面积以上的水柱中悬移质的水下重量。悬移质的单宽输沙率（以水下重量计）为gS′=，其中为悬移质垂线的平均运动速度。维持悬移质运动的能量虽然直接来自紊动动能，但后者来自水流的势能。考虑到水流势能已有一部分用来维持悬移质运动，可以写为Ws′ω=τ0u（1-eb）es，其中eb和es分别为维持推移质与悬移质运动的效率，u为平均流速。假定悬移质的运动速度和该点水流的速度相等，根据上述二式并结合水槽实验的结果可得。钱宁研究指出，eb=0.13，es=0.023～0.046，在水流的势能中，通过紊动支持泥沙悬浮的比例极微。

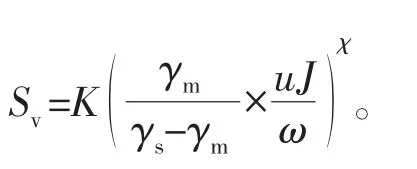
王明甫［21］、张浩［22］等的实验研究表明，高含沙水流的切应力为直线分布 τ=γm（h-y）J，其中 y为距离槽底的含沙水流水深。水面处τ=0，在槽底处τ=γmhJ。当无流核时，流速分布符合对数分布。即

如果挟沙水流中挟带的泥沙颗粒粒径较粗，就会增加水流中小尺度漩涡的强度，效果之一是使得水流的流速与能量分布更趋均匀，更小颗粒泥沙的浓度分布也更趋均匀。如果挟带的泥沙颗粒粒径较细，当含沙量达到一定程度时，就会形成网状结构，产生絮凝现象。这和含有高分子溶液的水流流动有本质的不同。由于高分子的长链结构有削减紊动猝发强度，使层流变厚，紊动强度减弱，减小紊动耗散的能量。含有高分子溶液的水流流动的特征与其说类似于淤泥质床面上水流的流动特征，毋宁说更类似于掺气水流的流动特征。高含沙水流的网状结构本质上是泥沙颗粒之间的电化学作用的结果，在网状结构遭到破坏后，起不到削减紊动猝发的作用。与刚性明渠水流流动相比，高含沙水流、掺气水流和淤泥质床面上水流的流动的共同特征是，改变了内部流体之间的能量传递和生成过程以及内外层流动之间的互相作用过程。但他们之间有本质区别。这方面缺乏实验数据的定量对比分析。

5 泥沙运动与水流作用分析及进一步研究的问题

练继建等［24］的淤泥质床面的清水流动阻力实验表明，流速分布的卡门常数保持不变，减阻或增速与雷诺数以及泥床特征等因素有关。淤泥质床面的水流紊流强度以及概率密度分布特征在外层区域的大小以及分布和刚性床面类似，只是在近壁区略有变化。淤泥质床面有抑制紊流猝发产生的作用，使得水流运动的紊动能量向低频区集中，能量耗散率减小。

关于悬移质含沙水流的减阻问题，目前学术界尚未定论。大致看法是，粒径小于0.06 mm的泥沙具有减阻作用。可能原因是加入细颗粒含量的挟沙水流的动力粘性增加，同时比重增大，而运动粘性系数反而减小，减弱了小涡的脉动强度，使得能耗损失降低。由于细颗粒泥沙的粒径较小，容易形成网状结构，这时运动流体的结构类似于含有高分子溶液的结构。不同之处在于，究竟含沙水流的哪一粒径在哪一含沙浓度下对紊流起到减阻作用，还需要进行系统的实验研究。与掺气水流运动的减阻机制相比，含沙水流的减阻机制可能影响紊动生长过程。目前人们对掺气水流运动减阻的通俗理解是气体分子增加流块之间的滑动，使得流层之间由滑动摩擦减小为滚动摩擦。由于气泡的体积容易变化，这种效果容易在流体内部多处发生。含有细颗粒的挟沙水流的减阻，可能与细颗粒泥沙表面的吸附作用有关，形成类似掺气水流中气泡的效果。但是细颗粒泥沙消耗紊动动能，和清水水流相比，会改变流动内部的能量分配过程。

式中：εm为挟沙水流紊动交换系数或挟沙水流的紊流粘性系数；ρm为挟沙水流的密度。Richardson数的物理意义是单位水体在单位时间内所提供的能量中，用以克服垂向密度梯度所消耗的能量所占的比例。Richardson数越大，卡门常数κ越小。钱宁认为，卡门常数κ的减小反映了含沙水流中紊动尺度的减小。虽然在天然河道上，较高的含沙量往往出现于洪峰期间，这是因为较高的流速夷平了沙纹、沙垄等床面形态，减小了河道的糙率，并非是较高的含沙量造成河道阻力的减小。

河床形态中，沙纹和沙垄等床面形态对阻力有显著影响。高含沙水流流动过程中，特殊的内部能量分配过程容易夷平这些床面形态，减小阻力，曾有专家建议应用这一特性治理黄河河道。推移质运动和高含沙水流流动中，流速分布的梯度增大而卡门常数值减小，实际上反映了涡旋级串和能量级串生成过程的特殊性质，是流动自相似性发生了变化，增加了中小尺度的紊动。从数学上看，是标度指数变小，也就是流动特性趋于均匀化。卡门常数的实质是对流动过程中自相似性的反映。小尺度涡旋的特性之一是增加耗散。含沙水流的密度较大，单位体积的高含沙水流储能较多，揭河底现象实际上是高含沙水流调整自身能量分配的一种方式，形成较清水水流更稳定的拟序结构。

对于推移质运动，沙粒的跃移运动要从水流中取得能量，除了一小部分还给水流之外，大部分转化为热能而损耗，这部分能量取自平均流势能，而不是紊动流能量，因而推移质运动的存在将增加水流的能量损失。对于悬移质而言，有了泥沙之后，水流的势能转化为热能的全过程将发生相应的变化。无论是清水水流或挟沙水流，拟序结构在能量级串的过程中起到了关键作用，是能量级串产生、维持、消亡过程的主要运动形式。由于紊流斑块和拟序结构、猝发等水流结构之间有密切关系，在强度指标上有很强的正相关性，对于推移质运动，可以以猝发和紊流斑块作为水流指标之一。具体的定量关系将另文论述。无论如何，挟沙水流和清水水流的能量级串都是流体流动过程中，在特定的初始条件和边界条件下，对于自身流动系统的一个自适应的调控过程。

与床面的沙波形态的影响相比，天然冲积河流中含沙量对阻力的影响只是一个次要因素。泥沙的存在影响水流条件，而水流条件改变后，又进一步影响泥沙的运动。由于天然河流中携带的是非均匀泥沙，细颗粒泥沙的存在对于粗颗粒泥沙的运动也会产生影响。细颗粒泥沙的存在会对水流的粘性产生影响，含沙量对水流粘性产生的影响要比其他因素大得多。实验表明，细颗粒泥沙的存在除了使得流速、含沙量分布的梯度变陡，即卡门常数κ减小外，还将使粗颗粒的输沙率显著增大。细颗粒含沙量愈大，粗颗粒的挟沙能力也愈大。挟沙能力Sm归结为对于下式的研究

式中：gT为单宽输沙率；B为河宽；h为水深；其他符号同上。对于式（29）在具体情形下的表达形式，不同学者得到不同的结果［25-28］，除了泥沙因素外，还与流速分布有关［29］。

在分析挟沙能力的过程中，有必要对以下问题作进一步研究：（1）挟沙水流的能量级串的实验量测及与清水水流的对比；（2）挟沙水流的阻力特性，包括和清水相比的减阻以及增阻机理及其定量规律；（3）使用统计和力学分析方法，精确描述推移质运动；（4）挟沙水流内外层流动之间的互相作用过程；（5）挟沙水流中涡的级串过程的特性；（6）非恒定、非均匀流对泥沙传输的影响。

6 结论

本文综述了挟沙水流的能量级串，尤其是推移质输运特性方面取得的研究成果，分析了挟沙水流的物理机制以及泥沙对水流运动特性的影响，对存在的若干问题进行了讨论，对有关研究方向进行了展望。

［1］钱宁，万兆慧.泥沙运动力学［M］.北京：科学出版社，2000.

［2］孙志林，祝永康.Einstein 推移质公式探讨［J］.泥沙研究，1991（1）：21-26.SUN Z L，ZHU Y K.A study on Einstein′s bed-load transport formula［J］.Journal of Sediment Research，1991（1）：21-26.

［3］高建恩.推移质输沙规律的再探讨［J］.水利学报，1993（4）：62-69.GAO J E.Revisit bed-load transport formula［J］.Journal of Hydraulic Engineering，1993（4）：62-69.

［4］万声淦，窦国仁.挟沙水流的紊流结构［J］.水利水运研究，1995（1）：89-102.WAN S G，DOU G R.Turbulent Structure of Sediment-laden Flow［J］.Journal of Hydro-Science and Engineering，1995（1）：89-102.

［5］毛野，杨华，袁新明.表面糙率与明渠紊流猝发现象［J］.水利学报，2002（6）：53-59.MAO Y，YANG H，YUAN X M.Bed surface roughness and bursting phenomena in open channel［J］.Journal of Hydraulic Engineering，2002（6）：53-59.

［6］刘兆存，徐永年.低含沙水流运动特性综述［J］.泥沙研究，1999（2）：72-78.LIU Z C，XU Y N.Review of properties of low concentration sediment flow［J］.Journal of Sediment Research，1999（2）：72-78.

［7］刘兆存，徐永年.高含沙水流运动特性综述［J］.泥沙研究，2001（4）：74-81.LIU Z C，XU Y N.Review of properties of hyper-concentrated flow［J］.Journal of Sediment Research，2001（4）：74-81.

［8］刘兆存，李勇，金生.明渠流动若干特性初探［J］.力学季刊，2007，28（2）：293-298.LIU Z C，LI Y，JIN S.Studies in some properties of open channel flow［J］.Chinese Quarterly of Mechanics，2007，28（2）：293-298.

［9］窦国仁.再论泥沙起动流速［J］.泥沙研究，1999（6）：1-9.DOU G R.Incipient motion of coarse and fine sediment［J］.Journal of Sediment Research，1999（6）：1-9.

［10］窦国仁，董风舞.潮流和波浪的挟沙能力［J］.科学通报，1995，40（5）：443-446.DOU G R，DONG F W.Sediment laden capability of tide and wave current［J］.Chinese Science Bulletin，1995，40（5）：443-446.

［11］Morrison J F，Subramanian C S，Bradshaw P.Bursts and the law of the wall in turbulent boundary layers［J］.J.Fluid Mech.，1992，241：75-108.

［12］Krogstad P A，Antonia R A，Browne L W B.Comparison between rough-and smooth-wall turbulent boundary layers［J］.J.Fluid Mech.，1992，245：599-617.

［13］SL′vov V，Procaccia I，Rudenko O.Universal model of finite Reynolds number turbulent flow in channels and pipes［J］.Physical Review Letters.PRL，2008，100：054504.

［14］Javier.The roll up of a vortex layer near a wall［J］.J.Fluid Mech.，1993，248：297-313.

［15］黄亦芬，窦国仁.高浓度均质紊流结构的试验研究［J］.水利水运科学研究，1989（1）：1-12.HUANG Y F，DOU G R.The mean structure of homogeneous hyperconcentrated fluid motion and its drag coefficient［J］.Journal of Hydro-Science and Engineering，1989（1）：1-12.

［16］王兆印，王兴奎，任裕民.宾汉体频谱分布特性的水槽实验研究［J］.水利学报，1993（4）：12-22.WANG Z Y，WANG X K，REN Y M.Statistic properties and spectral density distribution of Bingham fluid in open channel flow［J］.Journal of Hydraulic Engineering，1993（4）：12-22.

［17］Wang Xingkui，Qian Ning.Turbulence characteristics of sediment-laden flow［J］.Journal of Hydraulic Engineering，ASCE，1989，115（6）：781-800.

［18］Wan Zhaohui，Wang Zhaoyin.Hyperconcentrated flow［M］.Rotterdam：A.A.Balkema，Netherlands，1994.

［19］窦国仁，王国兵.宾汉极限切应力的研究［J］.水利水运科学研究，1995（2）：103-109.DOU G R，WANG G B.Study on Bingham yield stress of hyperconcentration fluid［J］.Journal of Hydro-Science and Engineering，1995（2）：103-109.

［20］乐培九.高含沙紊流的阻力及其输沙特性［J］.泥沙研究，1986（2）：17-25.YUE P J.Resistance and transport properties of sediment hyper-concentrated turbulent flow［J］.Journal of Sediment Research，1986（2）：17-25.

［21］王明甫，段文忠，谈广鸣，等.高含沙水流的水流结构及运动机理［J］.中国科学，1987（5）：549-560.WANG M F，DUAN W Z，TAN G M，et al.Structure and mechanism of hyper-concentrated flow［J］.Science in China，1987（5）：549-560.

［22］张浩，任增海.明渠高含沙水流阻力规律探讨［J］.中国科学，1982（6）：571-577.ZHANG H，REN Z H.Resistance laws of open channel hyper-concentrated flow［J］.Science in China，1982（6）：571-577.

［23］舒安平，费祥俊.高含沙水流挟沙能力［J］.中国科学，2008，38（6）：653-667.SHU A P，FEI X J.Sediment-laden Capability of hyper-concentrated flow［J］.Science in China，2008，38（6）：653-667.

［24］练继建，洪柔嘉.淤泥质床面的阻力特征［J］.科学通报，1994，39（19）：1 796-1 798.LIAN J J，HONG R J.Turbulence characteristics of drag-reducing flows over muddy beds［J］.Chinese Science Bulletin，1994，39（19）：1 796-1 798.

［25］Nino Y，Hgarcia M.Experiments on particle-turbulence interactions in the near-wall region of an open channel flow：implications for sediment transport［J］.J.Fluid Mech.，1996，326：285-319.

［26］Sechet P，Guennec B L.Bursting phenomenon and incipient motion of solid particles in bed-load transport［J］.Journal of Hydraulic Research，1999，37：683-696.

［27］Nakato T.Tests of selected sediment-transport formulas［J］.Journal of Hydraulic Engineering，1990，116（3）：362-379.

［28］Wang xinkui，Li danxun，Qu Zhaosong，et al.Verification and comparison of formulas for bed load transport［J］.Journal of Hydrodynamics，2001,13（1）：8-11.

［29］Liu Z C，Fan W J.Velocity distribution of wall bounded flow［J］.Journal of Zhejiang University，2010，11（7）：505-510.