三峡两坝间水田角河段航道整治三维水流数学模型应用研究*
2010-12-05冯小香李建兵樊建超
冯小香 ,李建兵 ,樊建超
(1.交通部天津水运工程科学研究所工程泥沙交通行业重点实验室,天津300456;2.清华大学水沙科学与水利水电工程国家重点实验室,北京100084;3.天津市引滦工程黎河管理处,遵化064200)
水田角河段是三峡两坝间“四滩一湾”中极具代表性的洪水急流滩(图1)。该滩上连陡山沱,岸线顺直,下连莲沱微弯河段。进口段较狭窄,横断面呈典型“V”型,最小宽度为380 m,滩下骤然展宽至650 m,展宽段有一个深沱,最大水深达90 m,河道深泓陡降40 m,而后又陡升50 m,进口至深沱断面过水断面面积由13 000 m2增大至 32 700 m2。
受两坝运行的影响,该河段枯水期水流平静,中水期流缓;当流量大于30 000 m3/s,河宽放宽处,强大的泡漩、大范围的回流同时存在,挤压主流带宽度不足河宽的1/3,水流湍急,流态紊乱,船舶航行较困难,是两坝间河段急需整治的重点河段之一。
以往研究中多采用物理模型和平面二维水流数学模型对急流滩段航道整治技术进行研究。如陆永军[1]采用平面二维数学模型对松花江三姓浅滩航道整治工程进行了研究;曹民雄[2]采用概化水槽试验、遥控自航船模上滩试验、平面二维水流数学模型及理论分析等技术手段,研究了山区河流急流滩险整治的相关技术问题;刘万利等[3]采用平面二维水流数学模型,对安康枢纽回水变动区河段滩险整治方案效果进行了论证;姚仕明等[4]采用三维水流模型模拟了两坝间河段的三维水流结构,但未对具体滩段的整治方案进行论证。本研究考虑到水田角河段具有弯道环流、回流、泡漩流等复杂水流流态特征,开发建立曲线坐标系下三维水流数学模型,对水田角河段航道整治效果进行论证分析。
1 三维紊流数学模型的建立
1.1 模型基本方程
平面曲线坐标、立面σ坐标系统下三维流动控制方程为
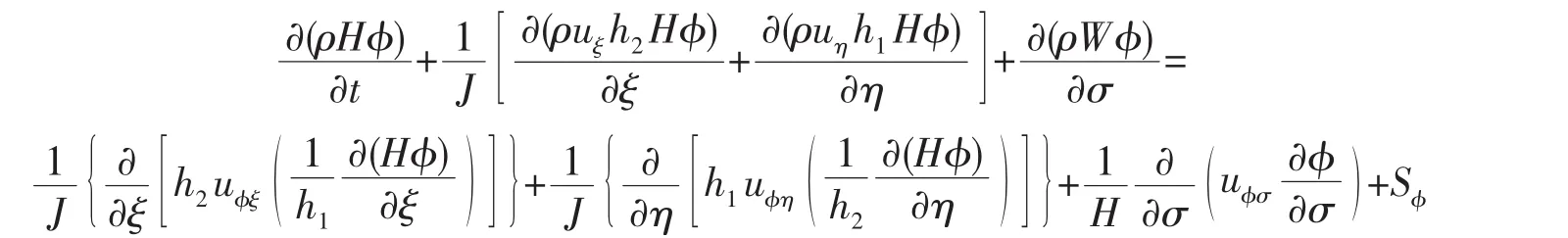
式中:t为时间;ρ为水流密度;H为水深;ζ为水位;J=h1h2,其中h1,h2分别为平面正交网格在ξ,η方向上的拉梅系数;uξ,uη,W 分别为模型坐标系数下水流在 ξ,η,σ 方向上的流速分量;φ 为 uξ,uη,W;输运方程源项 Sφ=SCφ+SPφφ。
σ坐标系下垂向伪流速W和实际垂向流速w之间的相互转化关系为
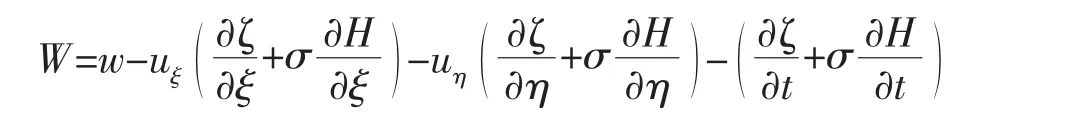
1.2 模型的定解条件
(1)初始条件。
综上可知:该项目地下室顶板开裂的主要原因为施工方法选择不当,混凝土水化热释放过程引起明显的板温度胀缩裂缝,该裂缝为非受力裂缝,影响结构后期正常使用,不影响结构整体安全性.
给定计算域各点初始速度场、k,ε分布,各节点初始水位,并令动水压力为0。
(2)自由表面边界条件。
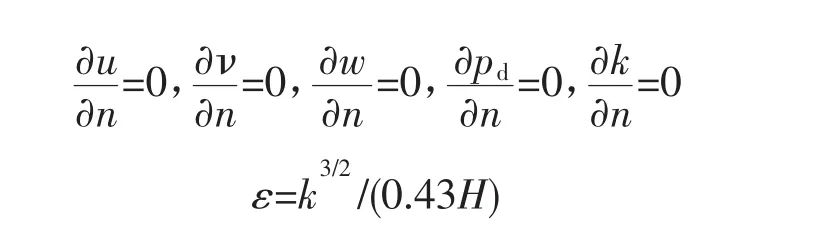
(3)进口边界条件。
上游进口条件一般采用流量控制条件。公式为
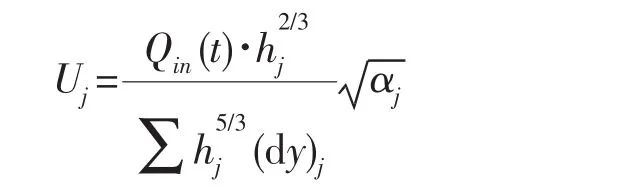
式中:下标j表示沿y方向网格计算点。计算出垂线平均流速沿河宽分布,进一步可按均匀分布或按对数律计算流速沿水深的分布。
(4)出口边界条件。
出口条件采用水位控制,即给定ζ(t),各变量沿出流边界的垂直方向梯度为0。
(5)壁边界条件。
根据固边界不可入原理,取法向流速为0。底部应力(τbx,τby)由下式计算
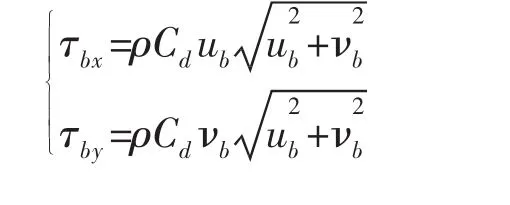
由对数壁面律定理,(ub,νb)满足
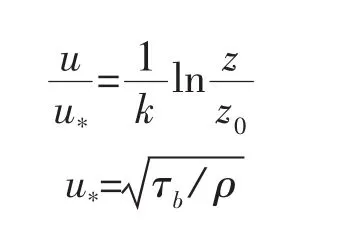
由此可得
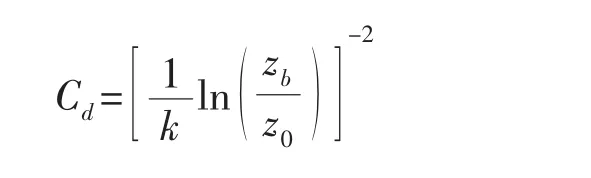
2 三维水流数学模型的验证
采用物理模型实测资料对水田角河段三维水流结构进行验证。研究河段长约2.5 km,共划分91×31×20个网格,河段三维地形见图1。试验流量为40 000 m3/s,模型出口水位65.75 m(对应葛洲坝运行水位63 m)。纵向网格尺度23~37 m,横向网格尺度14~28 m(图2),垂向网格尺度在0.01~5.5 m。
图3给出了水田角河段典型断面(3d2、3d3、3d4、3d5)3个方向流速的计算值与实测值对比情况,其中u方向为顺水流流动方向,v方向为水流横向流速(右岸→左岸)方向,w为水流垂向(垂直向上)(下同)。由图3可以看出,除个别断面存在较大误差外,总体上模型计算值与实测值基本一致,表明模型具备模拟复杂河段三维流动特性的能力。

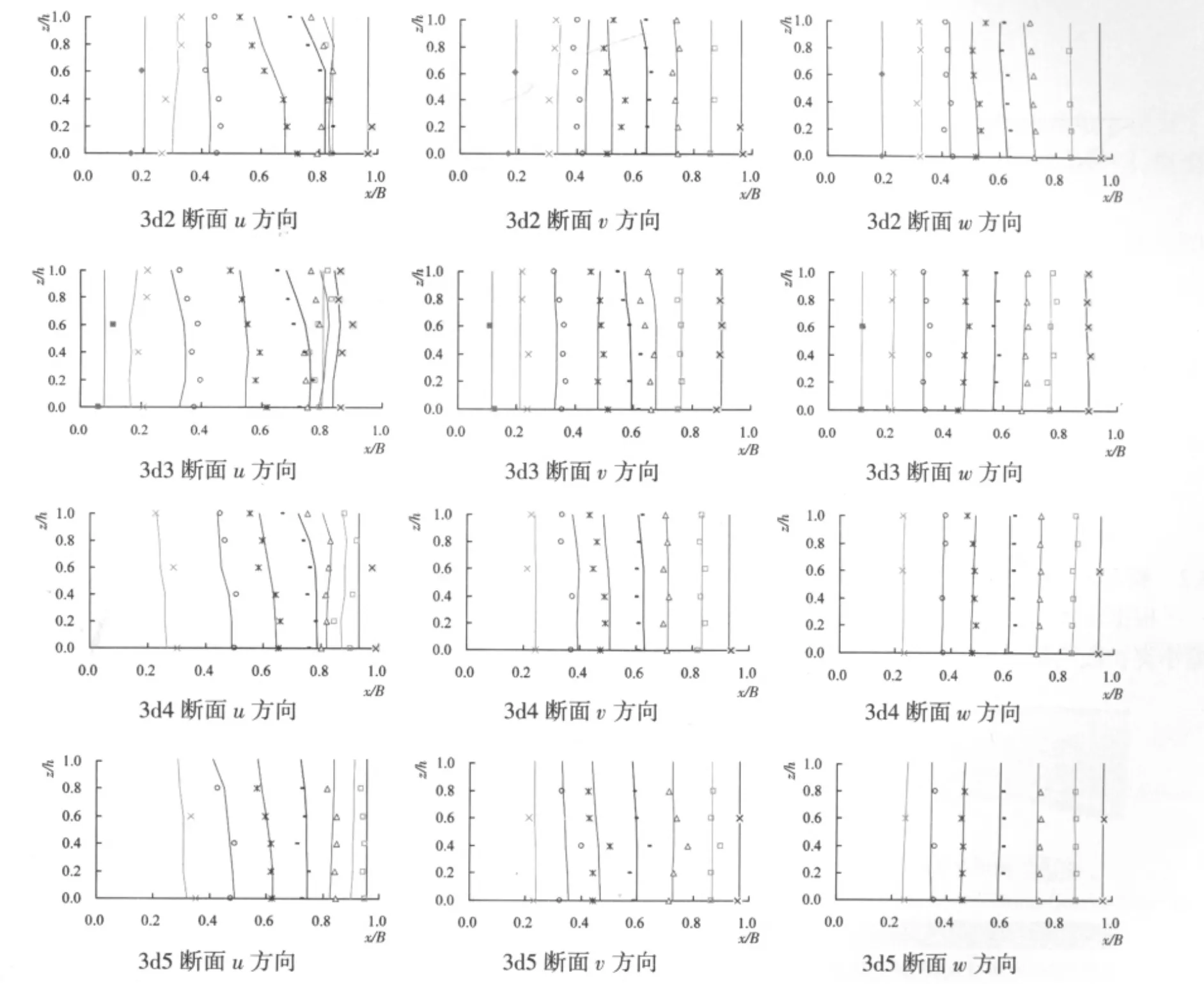
图3 典型断面计算流速与实测流速对比图Fig.3 Comparison with computed and measured velocity
3 水田角河段航道整治方案论证
3.1 现状流场分析
图4给出了研究河段整治前表层、底层的流场图。图5给出了典型断面横断面流场图(横断面位置见图2)。由图4和图5可以看出,由于水田角河段地形复杂,在弯顶左右两侧均形成较大范围的回流区,弯顶处的表底层水流流向基本保持一致,弯顶下游底表层水流流向表现出弯道水流的特性,即底部流速方向偏向右岸(凸岸),表层流速偏向左岸(凹岸)。同时,弯道环流的强度及分布与河道弯曲半径以及局部地形等因素有关,地形复杂的横断面除存在较大的环流外,两边还存在小的环流。
由图4和图5还可以看出,表层流速略大于中层流速,两者差别较小,表层流速可以近似代表表层3.5 m水深(船舶吃水深度)范围内的平均流速场。当来流流量为35 000 m3/s、葛洲坝运行水位63 m时,水田角河段主流带流速均大于3.0 m/s,局部存在大于3.5 m/s的流速区。在水田角弯顶附近,水流形成对峙卡口,流态紊乱,对船舶航行不利。

3.2 整治方案实施后流场分析
根据现状情况下河段水流流态,从水流条件对船舶航行影响的角度出发,可考虑采取一定的工程措施,缩小突扩段两侧回流,增加主流带宽度,降低主流带流速。拟采取的整治工程方案[5-6]见图6。
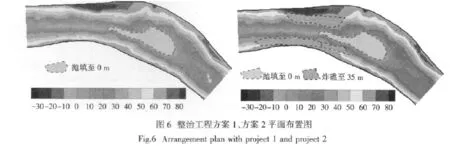
方案1:将深槽填至0 m等深线;方案2:在整治方案1的基础上,对突扩段上游两侧进行炸礁,在图6所示炸礁范围内,炸至35 m高程,进一步调整水流进入突扩段的水流横向分布,削减地形对水流的约束作用。
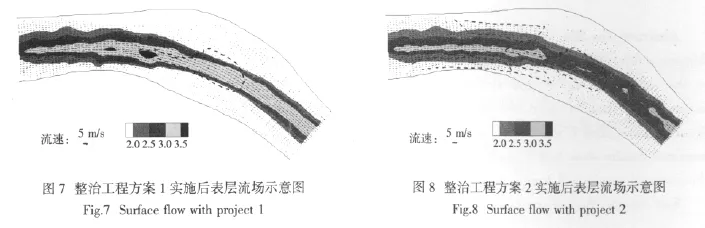
整治方案实施后的表层流场分别见图7和图8。由图7和图8可以看出,在方案1工程作用下,水田角河段突扩段主流带宽度有所增加,两侧回流区范围有所减小,回流流速减小,航道水流条件得到一定程度的改善。从横断面二次流情况来看,工程断面(2#横断面)二次流流速明显减小,流态明显改善;在方案2工程作用下,水田角河段主流带宽度明显增加,流速明显减小,突扩段流速均小于3.0 m/s,两侧回流区明显减小,回流区流速明显减小,工程效果较方案1有明显改善。整治工程方案2的布置能够较好地改善水田角河段局部水流流态,有利于船舶的安全航行,可以达到整治的目的。
4 结语
(1)采用平面曲线拟合坐标系及垂向σ坐标系,利用交错网格,建立曲线坐标系下三维水流数学模型。
(2)采用三峡两坝间物理模型典型河段的三维流速资料,对模型进行进一步检验。检验结果表明,模型能够模拟复杂河道边界和地形条件下的三维水流流动,可用于局部河段整治方案试验研究。
(3)利用已建的曲线坐标系下三维水流数学模型,对水田角河段天然情况下的水流结构进行数值模拟和分析。分析结果表明,水田角河段水流具有明显的弯道环流特征,在弯顶下游断面均呈现明显的断面二次流,其表流由凸岸指向凹岸,底流由凹岸指向凸岸。
(4)影响水田角河段水流流态的关键因素是来流大小、局部地形、河道特性等。研究基于调整水流流速分布、减小回流的整治原则,对研究河段的整治工程方案进行探讨性研究,并对不同的试验方案分别进行了三维水流数值模拟研究。研究结果显示,炸礁、抛填等整治措施的综合运用能较有效地改善水田角等河段的局部水流流态,可以达到整治目的。
[1]陆永军.松花江三姓浅滩航道整治的二维数值模拟研究[J].泥沙研究,1998(2):26-35.LU Y J.2-D numerical simulation on waterway regulation of Sanxing shoal on the Songhuajiang River[J].Journal of Sediment Research,1998(2):26-35.
[2]曹民雄.山区河流急流滩险航道整治技术研究[D].南京:南京水利科学研究院,2005.
[3]刘万利,李一兵,崔喜凤,等.安康枢纽回水变动区航道整治数学模型研究[J].水道港口,2007,28(3):173-177.LIU W L,LI Y B,CUI X F,et al.Study on mathematic modeling of channel regulation in fluctuating backwater zone of Ankang hydro-junction[J].Journal of Waterway and Harbor,2007,28(3):173-177.
[4]姚仕明,王兴奎,张超,等.两坝间河段通航水流条件的三维数值模拟[J].水科学进展,2007,18(3):374-378.YAO S M,WANG X K,ZHANG C,et al.3-D numerical simulation of navigable flow conditions between Three Gorges Dam and Gezhouba Dam[J].Advances in Water Science,2007,18(3):374-378.
[5]郝品正.三峡两坝间大流量复杂水流下航运安全关键技术研究报告[R].天津:交通运输部天津水运工程科学研究所,2009.
[6]冯小香,孔宪卫,张丽.三峡~葛洲坝两坝间大流量下非恒定水流水力特征及其对通航条件影响数值模拟研究报告[R].天津:交通运输部天津水运工程科学研究所,2009.
